• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вправа.

1. Довести, що Х(п) є Кь

2. Довести, що (незміщена).

6. Порівняти оцінки в середньоквадратичному.

3.4 Асимптотика нормальніше оцінки (АНО)

Для того, щоб вміти порівнювати оцінки вигляду 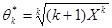(див. приклад 4), среднеквадратического підходу недостатньо: другий момент такої випадкової величини порахувати навряд чи вдасться. Оцінки такого вигляду (функції від сум) вдається порівнювати за допомогою асимптотичного підходу. Більш точно цей підхід застосовний до так називається «асимптотика нормальним» оцінкам.

Хай ХІ..., Хп — виборка обєма п з параметричного сімейства розподілів Уд, в є в.

Визначення 11. Оцінка q* називається асимптотично нормальною оцінкою параметра q з коефіцієнтом s²(q) якщо

Приклад 11. Хай ХІ..., Хп — вибірка обєма п з рівномірного розподілу U0q, де q > 0.
Перевіримо, чи є оцінки q* = 2Х iq = Х(n) асимптотиxно нормальними (АНО). По ЦПТ

Та оцінка q* = 2Х асимптотика нормальна з коефіцієнтом а2(в)= 4С>дХІ = 46>2/12 = 6>2/3.
Для оцінки q = Х(n) маємо:

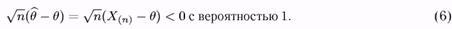
Таким чином, оцінка в = Х(П) асимптотика нормальної не є.

Залишилося відповісти на питання що напрошуються:

1) Куди все ж таки сходиться по розподілу Ön(X(n)- q)?
Вправа. Довести,що Ön(X(n)- q)Þ0.

Порядок дій:Виписати визначення слабкої збіжності. Намалювати функцію розподілу нуля. Знайти за визначенням функцію розподілуÖn(X(n)- q)_. Переконатися, що вона
сходиться до ф.р. нуля у всіх точках неперервності останньої. Не забудьте про існування замечательних меж, логарифмів й ряду Тейлора.

2) Якщо Ön(X(n)- q)Þ0, то на який ступінь п потрібно спробувати помножити, щоб одержати збіжність до величини, відмінної від 0 й оо?

Вправа.Довести, що Ön(X(n)- q)Þh, причому величина —h має показове розподілення Е1/0.

Порядок дій:колишній.

3) Для оцінки 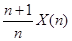властивість (6) не виконано. Чи може ця оцінка бути АНО?

Вправа.Модифікувати міркування й довести, що ця оцінка теж не є асимптотика нормальною.

4) Чи погано, що оцінка q = Х(n) не асимптотика нормальна? Може бьіть, збіжність Ön(X(n)- q)Þh ще краще?

Попробуєм відповісти на останнє питання.

Читайте також:

1. Вправа.
2. Вправа.

Переглядів: 689