• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Єдиність еффективної оцінки в класі з фіксованим зсувом

Теорема7. Якщо q₁* є Кь і q₂^*є Кь — дві еффективні оцінки в класі Кь, то з вірогідністю 1 вони співпадають: Рд(q₁* = q₂^*)= 1.

Доказ теореми 7. Закиданням спочатку, що Еq (q* - q) ² = Еq (q2* - q)². Дійсно,
оскільки q1* еффективна в класі Кь, то вона не гірше за оцінку q2*, тобто

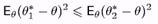
і навпаки. Тому Еq (q1* - q) ² = Еq (q2* - q) ^2.

Розглянемо оцінку 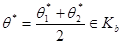(довести!). Вичислим її средньоквадратичне відхилення.

Помітимо, що

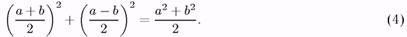
Покладемо а = в* - 9, Ь = 9% - 9. Тоді (а + Ь) /2 = 9* - 9, а - Ь = в* - 9%. Підставимо ці вирази в (4) й візьмемо математичні очікування обох частин:

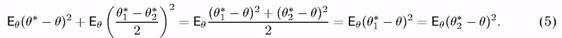
Але оцінка q* належить Кb, тобто вона не краща, наприклад, еффективної оцінки q*. тому

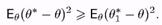
Порівнюючи цю нерівність з рівністю (5), бачимо, що

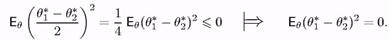
Тоді (чому?) Рq (q₁* = q₂^*)= 1, що й було потрібне довести.

Для прикладу розглянемо порівняння двох оцінок. Зрозуміло, порівнюючи оцінки попарно між собою, якнайкращої оцінки в цілому класі не знайти, але вибрати кращу з двох теж корисно. А способами пошуку як найкращої в цілому класі теж скоро займемося.

Приклад 10.Хай ХІ..., Хп — вибірка обєму п з рівномірного розподілу Uо, q, де q > 0.Тоді q = Х(n)= mах{ХІ...,Хп}— оцінка максимальної правдоподібності, а q* = 2Х — оцінка
методу моментів, одержана по першому моменту. Порівняємо їх в середньоквадратичному. Оцінка q* = 2Хнезміщена (див. приклад 4), позтому

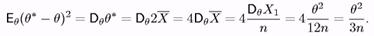
Для q = Х(n)= тах{ХІ..., Хп} маємо

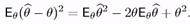
Порахуємо перший й другий момент випадкової величини в = Х(п). Знайдемо (корисно пригадати, як це робилося в минулому семестрі!) функцію розподілу й густина q:

тому

При п = І квадратичні відхилення рівної, а при п > І

то є Х(n) краще, ніж 2Х. При цьому Eq(X(n)- q)² ® 0 із швидкістю n^-2, тоді як Еq (2Х - q) ®0 із швидкістю n^-1.

Читайте також:

1. Аналіз відхилень – основний інструмент оцінки діяльності центрів відповідальності
2. Аналіз відхилень — основний інструмент оцінки діяльності центрів відповідальності
3. Аналіз методичних підходів до оцінки конкурентоспроможності фірми
4. Атестація як особливий метод оцінки персоналу
5. Аудиторський ризик і методи його оцінки
6. Бази оцінки, відмінні від ринкової вартості
7. В якості критеріїв для оцінки або вимірювання предмета завдання з надання впевненості не можуть використовуватись очікування, судження або власний досвід аудитора.
8. Вибір системи обліку оцінки діяльності підприємства
9. Види вартісної оцінки продукції сільського господарства
10. Види оцінки ефективності інвестиційного проекту
11. Види оцінки основних засобів.
12. Види оцінки основних фондів

Переглядів: 698