• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Средньоквадратичний підхід. Eфективності оцінок

Способи порівняння оцінок

З Порівняння оцінок

Використовуючи метод моментів й метод максимальної правдоподібності, ми отримали для кожної параметра вже досить багато різних оцінок. Яким же чином їх порівнювати? Що повинне бьіть показником «відмінно» оцінки?

Зрозуміло, що чим далі оцінка відхиляється від параметра, тим вона гірше. Але величина \q* q\ для порівняння непридатна: во-первьіх, параметр qневідомий, по-друге, q* випадкова величина, так що ці величини звичайно порівняти не можна. Як, наприклад, порівнювати \Х - q\ і \Х^к q¦? Або, на одномузлементарном виході, ¦2.15 - q\ і ¦3.1 - q¦?

Тому має смисл порівнювати не відхилення як такі, а середні значення тих відхилень,тобто Е₀¦q* -q\.

Але математичне очікування модуля с.у. вважати звичайно скрутне, тому більш зручною
характеристикою для порівняння оцінок вважається Е_q (q* - q)² . Вона зручна ще й тим, що дуже чуйно реагує на малоймовірні, але великі по абсолютному значенню відхилення q* від q (зводить їх в квадрат).

Помітимо ще, що Е_q(q* - q)² є функція від q, так що порівнювати ці «середньоквадратичні» відхилення треба як функції від в поточечно. Такий підхід порівнянню оцінок називається средньоквадратичним.

Зрозуміло, в залежності від потреб дослідника можна користуватися й іншими характеристиками.

Існує й так званий асимптотичний підхід до порівняння оцінок, при якому для порівняння оцінок використовується деяка характеристика «розкидання» оцінки відносно параметра при більших п.

Нехай ХІ,..., Хп вьіборка обгема п з параметричного сімейства розподілів, ¦_q де qє Q.

Визначення8. Кажуть, що оцінка q₁ краще за оцінку q₂ в смислі середньоквадратичного підходу, якщо для будь-кого qє Q

й хоч би при одному q ця нерівність строга.

Оцінки можуть бути непорівнювані: наприклад, при деяких qЕq (q* - q)² £ Еq (q₂^* - q)², при інших q - навпаки.

Чи Існує серед всіх оцінок найкраща в смислі середньоквадратичного підходу? Скептик зі
схильністю до філософії відразу відповість «немає». Доведемо, що він правий.

Теорема 6.У класі всіх можливих оцінок найкращої оцінки в смислі среднеквадратического підходу не існує.

Доказ теореми 6.Пусть, навпаки, q* найкраща, то єсть для будь-який інший оцінки q?, при будь-якому qє Q

Нехай q1 довільна точка Q. Роздивимось оцінку (статистику) q*1 = q1. Тоді

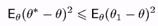
при будь-якому q є Q. Візьмем q = q1 є Q і отримаємо наступну нерівність:

тому Еq1 (q* - q1)^{2 =} 0. Внаслідок довільності q1 це виконується при будь-якому q є Q:

Але зто можливо тільки якщо q* = q(оцінка в точності відгадує невідомий параметр). Тобто q* навіть не є статистикою. Такого типа приклади привести можна, але математичній статистиці тут робити нічого.

Вправа.Обгясніть словесно доказ теоремьі 6.

Якщо в дуже широкому класі всіх оцінок якнайкращої не існує, то, можливо, слід звузити клас рассматриваемьіх оцінок (або розбити клас всіх оцінок на окремі підкласи й в кожному шукати якнайкращу).

Як правило розглядають оцінки, що мають однаковий зсув b(q)= Е_qq* — q. Позначимо через К класе оцінок, що мають зсув Ь(в\.

Тут До — класі незміщенних оцінок.

Визначення 9.Оцінка q* є Кь називається еффективною оцінкою в класі Кь, якщо вона краще (не гірше) всіх інших оцінок класа_Кь в смислі середньоквадратичного підходу. Тобто для будь-кого q* єКь
для будь-кого qє Q

Визначення 10.Зффективна оцінка в класі К₀ (незміщенних оцінок) називається просто зффективною.

Зауваження 10.Для q* є К_b, за визначенням дисперсії, Е_q(q* - q) ² = Еq (q* - Еqq*)² =Dqq*,так що порівняння в середньоквадратичному несмещенньїх оцінок — зто порівняння їх дисперсії. Тому еффективну оцінку (в класі К₀) часто називають «незміщеною оцінкою з рівномірно мінімальною дисперсією». Рівномірність мається на увазі по всіх q є q. Для q* є К_b

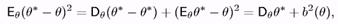
отже порівняння в середньоквадратичному оцінок з одинаковим зсувом — це також порівняння їх дисперсії.

Вправа.Ми збираємося шукати якнайкращу оцінку в класі Кь. Обясніть, чому доказ теореми 4 не пройде в класі Кь.

Читайте також:

1. Асимптотичний підхід до порівняння оцінок
2. Багаторівневий підхід. Протокол. Інтерфейс. Стек протоколів.
3. Бальна система оцінок технічного стану газопроводів
4. Вибір алгоритмів розрахунку комплексних порівняльних оцінок.
5. ВИДИ ЕКСПЕРТНИХ ОЦІНОК
6. Види педагогічного оцінювання і педагогічних оцінок.
7. Відповідність рейтингових оцінок за окремі види навчальної роботи у балах оцінкам за нац. шкалою
8. Для отримання кінцевого результату (експертних оцінок) використовують анкетні методи і методи групової експертизи.
9. Експертних оцінок.
10. Європейська шкала оцінок
11. Запаси відображаються в бухгалтерському обліку і звітності за найменшою з двох оцінок: первісною вартістю або чистою вартістю реалізації.
12. Комплексний підхід.

Переглядів: 786