• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Питання і вправи

Вправа.

1) Пересвідчитися, що відрізок [Х_(n) - 5, Х₍₁₎] не пустий.

2) Знайти оцінку методу моментів (по першому моменту) і пересвідчитися, що вона відрізняється від ОМП.

3) Знайти ОМП параметра qрівномірного розподілу U_q,q+3 .

1. Задачник [1], задачі 2.1 - 2.16.

2. Дана вибірка Х₁,..., Х_n , X_i Î В_p, р Î (0,1) невідомий параметр. Перевірити, що Х₁, Х₁Х₂,
X₁(1 - Х₂) є незміщеними оцінками відповідно для р, р², р(1 - р). Чи Є ці оцінки спроможними?

3. Дана вибірка Х₁,..., Х_n, X_i Î П_l, l > 0 невідомий параметр. Перевірити, що X₁ і I(X₁ = k) є незміщеними оцінками відповідно для l і 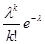. Чи Є ці оцінки спроможними?

4. Дана вибірка Х₁,..., Х_n, X_i Î U_0,q, q > 0 - невідомий параметр. Перевірити спроможність
і незміщеність оцінок: q₁^* = Х_(n), q₂^* = 2X, q₃^* = Х_(n) + Х₍₁₎.

5. Побудувати оцінки невідомих параметрів по методу моментів для наступних розподілів:

а) В_p по першому моменту,

б) П_l по першому і другому моменту,

в) U_a,b по першому і другому моменту,

г) Е_a по всіх моментах,

д) e_1/a по першому моменту,

е) U_-q,q як вийде,

ж) Г_a,l по першому і другому моменту,

з) N_a,s2 (для s² при a відомому і при a невідомому).

6. Які з оцінок в задачі 5 незміщені? спроможні?

7. Порівняти вигляд оцінок для параметра а, отриманих по першому моменту в задачах 5(г) і 5(д). Доказати, що серед них тільки одна незміщена. Вказівка. Використати властивість: якщо x ³ 0 п.н., то = const п.н.

8*. Довести властивість із задачі 7, використовуючи нерівність Коши-Буняковского-Шварца: 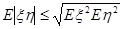, яке звертається в рівність Û êxô=сôhô (див. доказ властивості коефіцієнта кореляції ôрô£ 1 в курсі теорії імовірностей).

9. Побудувати оцінки невідомих параметрів по методу максимальної правдоподібності для наступних розподілів: а) Вр, би)П_n+1, в) U_{0,2 г}) Е2n_+3, д) U, е) N(а відомо).

10. Які з оцінок в задачі 9 незміщені? спроможні?

Читайте також:

1. IV. Питання самоконтролю.
2. V. Питання для самоконтолю
3. V. Питання туристично-спортивної діяльності
4. VI . Екзаменаційні питання з історії української культури
5. А.1 Стан , та проблемні питання застосування симетричної та асиметричної криптографії.
6. Акробатичні вправи
7. Акробатичні вправи.
8. Актуальні питання управління земельними ресурсами та їх охорони
9. Аналогія права - вирішення справи або окремого юридичного питання на основі принципів права, загальних засад і значення законодавства.
10. Бесіда за запитаннями.
11. В лекції висвітлюються питання використання мережних структур, їх недоліки та переваги.
12. Виділення в природних комплексах незвичайних, унікальних ділянок і явищ і питання їх збереження.

Переглядів: 576