Number Theory and its Founders

Mathematics is the Queen of Science and

Arithmetic is the Queen of Mathematics.

Gauss.

The theory of numbers, one of the oldest branches of maths, has engaged the attention of many gifted mathematicians during the past 2300 years. The Greeks, Indians and Chinese had made significant contributions prior to 1000 A.D. and in more modern times the subject has been developed steadily since Fermat, one of the fathers of maths.

In view of the diversity of problems and methods grouped together under the name of number theory, it is impossible to write even an introductory treatment which in any sense covers the field completely. The properties of the series of natural numbers, one of the basic and most essential concepts of maths, are the object of the theory of numbers. One finds that there exist many simple rules regarding numbers that are quite easy to discover and not too difficult to prove.

However, number theory also includes an abundance of problems whose content can be comprehended and expressed in simple terms, yet whose solution has for centuries defied all math investigation. Other problems whose solutions have been successfully obtained have yielded only to attacks by some of the most ingenious and advanced methods of modern maths.

The simplicity in form of its problems and the great variation in the methods and tools for their solution explain the attraction that number theory has had for mathematicians and laymen. The innumerable individual contributions, calculations, speculations, and conjectures bear witness to the continued interest in this field of maths throughout the centuries.

The origins of the study of number properties go back probably almost as far as counting and the arithmetic operations. It does not take long before it is discovered that some numbers behave differently from the others; for instance, some numbers can be divided into smaller equal parts and others not. The operations with fractions lead immediately to the study of divisibility of numbers, the least common multiple, and the greatest common divisor. Other approaches have led to early number-theory questions.

In number theory we are concerned with properties of certain of the integers ..., -3, -2, -1, 0, 1, 2, 3, ..., or sometimes with those properties of the real and complex numbers which depend rather directly on the integers. As in most branches of abstract thought, it is easier to characterize the theory of numbers extensively, by giving a large number of examples of problems which are usually considered as parts of number theory, than to define it intensively, by saying that exactly those problems having certain characteristics will be included in the subject.

The problems treated in classical number theory can be divided into groups according to a more or less rough classification. First, there are multiplicative problems, concerning with divisibility properties of the integers. It will be proved later that any positive integer n greater than 1 can be represented uniquely except for the order of the factors, as a product of primes, i.e., integers greater than 1 having no exact divisors except itself and 1. This may also be termed the fundamental theorem of number theory so manifold and varied are its applications. From the decomposition of 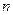into primes, it is easy to determine the number of divisors of .

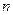In another direction, we have the problems of additive number theory: questions concerning the representability, and the number of representations of a positive integer as a sum of integers of a specified kind. For instance, upon examination it appears that some integers, like 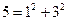and 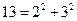, are representable as a sum of two squares; while others, like 3 or 12, are not. Which integers are so representable and how many such representations are there?

A third category may include what are known as Diophantine equations named after the Greek mathematician Diophantus, who first studied them. These are equations in one or more variables whose solutions must be integers, or at any rate rational numbers. For example, it is a familiar fact that 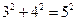which gives us a solution of the Diophantine equation 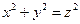. Giving a particular solution is hardly of interest; what is desired is an explicit formula for absolutions. A very famous Diophantine equation is that known as Fermat's equation: 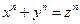. Fermat asserted that this equation has no solution (in nonzero integers, of course) if 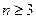; the assertion has never been proved or disproved for general 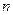. There is at present practically no general theory of Diophantine equations, although there are many special methods, most of which were devised for the solution of particular equations.

Finally, there are problems in Diophantine approximations. For example, given a real number 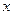and a positive integer 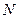, find that rational number 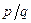for which 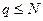and 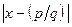is minimal. The proofs that 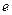and 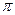are transcendental also fall in this category. This branch of number theory probably borrows the most from, and contributes the most to, other branches of maths.

The theorems of number theory can also be subdivided along entirely different lines – for example, according to the methods used in their proofs. Thus, the dichotomies of elementary and nonelementary, analytic and synthetic. A proof is elementary (although not necessarily simple!) if it makes no use of the theory of functions of a complex variable, and synthetic if it does not involve the usual concepts of analysis – limits, continuity, etc. Sometimes, but not always, the nature of the theorem shows that the proof will be in one or another of these categories.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
APPENDIX II	\|	Pierre de Fermat

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.002 сек.