• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Приклади розв’язання задач

Приклад 1. Визначити початкову активність А₀ радіоактивного магнію ²⁷Mg масою т = 0,2 мкг, а також активність А після закінчення часу t = 1 год. Передбачається, що всі атоми ізотопу радіоактивні.

Розв’язання. Початкова активність ізотопу

, (1)

де λ – постійна радіоактивного розпаду; N₀ – кількість атомів ізотопу в початковий момент (t = 0).

Якщо врахувати, що , , то формула (1) набуде вигляду:

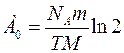. (2)

Виразимо величини в системі СІ та проведемо обчислення:

.

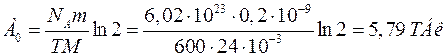Активність ізотопу зменшується з часом згідно із законом:

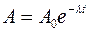. (3)

Замінивши у формулі (3) постійну розпаду λ її виразом, отримаємо:

.

Оскільки , то остаточно матимемо:

.

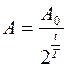Зробивши підстановку числових значень, одержимо:

.

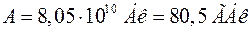Приклад 2.При визначенні періоду напіврозпаду Т_1/2 короткоживу­чого радіоактивного ізотопу використовується лічильник імпульсів. За час Δt = 1 хв від початку спостереження (t = 0) було налічено Δn₁ = 250 імпульсів, а у момент часу t = 1 год – Δn₂ = 92 імпульси. Визначити постійну радіоактивного розпаду λ і період напіврозпаду Т_1/2 ізотопу.

Розв’язання. Число імпульсів Δn, що реєструються лічильником за час Δt, пропорційне числу атомів ΔN, що розпалися. Таким чином, при першому вимірюванні:

, (1)

де N₁ – кількість радіоактивних атомів до початку відліку; k – коефіцієнт пропорційності (постійний для даного приладу і даного розташування приладу щодо радіоактивного ізотопу).

При повторному вимірюванні (передбачається, що розташування приладів залишилося тим самим):

, (2)

де N₂ – кількість радіоактивних атомів до початку другого вимірювання.

Розділивши співвідношення (1) на вираз (2) і врахувавши, що за умовою завдання Δt однакове в обох випадках, а також, що N₁ і N₂ зв'язані між собою співвідношенням , отримаємо:

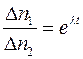, (3)

де t – час, що пройшов від першого до другого вимірювання. Для обчислення λ вираз (3) слід прологарифмувати:

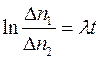, звідки:

.

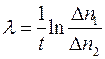Підставивши числові дані, одержимо постійну радіоактивного розпаду, а потім і період напіврозпаду:

;

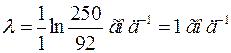Читайте також:

1. IV. Перевірка розв’язання і відповідь
2. Алгоритм розв’язання задачі
3. Алгоритм розв’язання розподільної задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі
10. Алгоритм розв’язування задачі оптимізації в Excel
11. АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОПТИМАЛЬНОГО РЕШЕНИЯ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛП
12. Аналіз задач і алгоритмів

Переглядів: 1593