• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задачі інцидентності на гранних поверхнях

До задач інцидентності відносять задачу побудови проекцій перерізів багатогранників площинами окремого положення, трактуючи її як задачу визначення проекцій сукупності точок, що одночасно належать граням багатогранника та заданій площині і являються вершинами фігури перерізу – опуклого багатокутника. На рис. 3.4 а) показана призма, зрізана фронтально-проекціювальною площиною α. Утворена фігура перерізу – чотирикутник 1234, вершинами якого є точки перетину ребер призми з площиною. Оскільки січна площина займає проекціювальне положення, то фігура перерізу має фронтальну проекцію 12223242, яка збігається з виродженою проекцією площини α2 в межах проекції багатогранника (див. рис.3.4, б). Горизонтальна проекція перерізу 11213141 визначена за умови належності вершин чотирикутника ребрам призми, яки займають горизонтально-проекціювальне положення, тому вона збігається з горизонтальною проекцією призми.

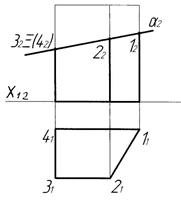
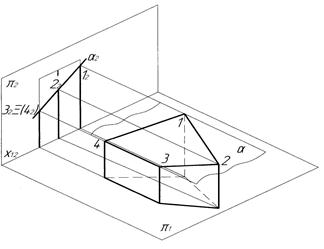
а) б)

Рисунок 3.4 - Переріз призми

Побудова перерізу піраміди площиною β показана на рис.3.5, а. Як і у випадку побудови перерізу призми, фігурою перерізу піраміди є чотирикутник. Його вершинами є точки перетину площини з ребрами. Січна площина β займає горизонально-проекціювальне положення. Тому фігура перерізу має горизонтальну проекцію 11213141, яка збігається з виродженою проекцією площини β1 в межах відповідної проекції піраміди (див. рис.3.5,б). Фронтальна проекція шуканого перерізу 12223242 визначена за умови належності кожної його вершини відповідному ребру піраміди.

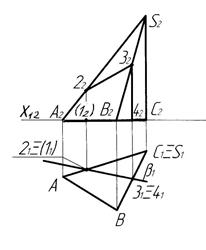
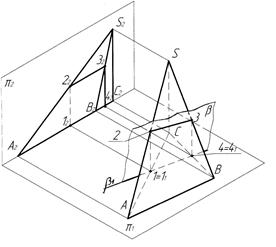
а) б)

Рисунок 3.5 - Переріз піраміди

До задач інцидентності можна віднести і задачу побудови проекцій наскрізних отворів в гранях багатогранників, оскільки її розв’язування базується на побудові проекцій точок за умови їх належності відповідним граням (включаючи ребра) багатогранника. На рис. 3.6,а показано принцип утворення наскрізного отвору в бічних гранях піраміди. Фронтальна проекція такого отвору має вироджену проекцію у формі трикутника ( див. рис. 3.6,б). Горизонтальна проекція визначена шляхом проведення допоміжних ліній в гранях піраміди, розглядаючи таким чином отвір як сукупність точок, що належать певній з граней.

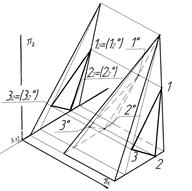
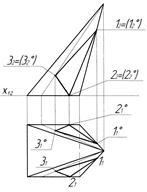
а) б)

Рисунок 3.6 - Наскрізний отвір

Читайте також:

1. Алгоритм розв’язання задачі
2. Алгоритм розв’язання розподільної задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз інформації та постановка задачі дослідження
11. Аналіз перед розв’язуванням задачі
12. Аналіз перед розв’язуванням задачі

Переглядів: 639