• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Складне нарахування, яке має цілу кількість періодів нарахування процентів.

Для розуміння і засвоєння механізму складного нарахування процентів (англ. compound interest) проаналізуємо й розв’яжемо Модельну задачу 2 (умова ─ жирним шрифтом, пояснення до задачі ─ звичайним).

Ви вклали в комерційний банк 1000 грн. на строк 4 роки під 10% річних на умові щорічного складного нарахування процентів.Внесок (вклад) грошей на від-критий у банку на своє ім’я рахунок, має назву – депозит-ний вклад. Відкриття депозитного рахунку на умові щоріч-ного складного нарахування процентів означає, що напри-кінці кожного року Ви не будете одержувати в банку про-центи. Ці проценти Ви будете залишати наприкінці кожно-го року на своєму рахунку, і на них будуть нараховуватися проценти таким же чином, як і на вкладені перші 1000 грн. Наприкінці четвертого року Вам повернуть Ваші 1000 грн., вкладені на початку першого року та проценти, нараховані за всі 4 роки.Потрібно знайти фактичну загальну суму грошей, що Ви одержите по закінченні чотирьох років.

Розв’язання Модельної задачі 2 включає розглядфінансової операції по періодах нарахування процентів.

В умові задачі період нарахування процентів ─ рік.

ПЕРІОД 1 (перший рік): на початку першого року Ви поклали на депозит 1000 грн; наприкінці першого року Ви маєте на депозитному рахунку 1100 грн:

─ розрахунок в періоді 1: 1000 грн + 1000 грн 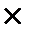0,1 = = 1000 грн (1+0,1) =1100 грн.

Дія: 1000 грн 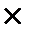0,1 = 100 грн ─ це розрахунок Вашого процента за перший рік. Ваш процент за перший рік залишається в банку на Вашому депозитному рахунку. На початок другого року у Вас на депозитному рахунку вже 1100 грн.

ПЕРІОД 2 (другий рік): наприкінці другого року Ви маєте на депозитному рахунку 1210 грн:

─ розрахунок періоду 2: 1100 грн + 1100 грн 0,1 = = 1100 грн 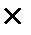(1+0,1) = 1210 грн.

Даний розрахунок можна провести інакше:

1000 грн · (1+0,1)·(1+0,1) = 1000 грн · (1+0,1) ² = = 1000 грн · 1,21 = 1210 грн.

На початок третього року у Вас на депозитному рахунку вже 1210 грн.

ПЕРІОД 3 (третій рік): наприкінці третього року Ви маєте на депозитному рахунку 1331 грн:

─ розрахунок періоду 3: 1210 грн + 1210 грн 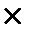0,1 = = 1210 грн 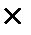(1+0,1) = 1331 грн.

Даний розрахунок можна провести інакше:

1000 грн(1+0,1)·(1+0,1)·(1+0,1) = 1000 грн · (1+0,1) ³ = = 1000 грн · 1,331 = 1331 грн.

На початок четвертого року у Вас на депозитному рахунку вже 1331 грн.

ПЕРІОД 4 (четвертий рік): наприкінці четвертого року Ви маєте на депозитному рахунку 1464,1 грн:

─ розрахунок періоду 4: 1331 грн + 1331 грн 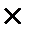0,1 = = 1331 грн (1+0,1) = 1464,1 грн.

Даний розрахунок можна провести інакше:

1000 грн · (1+0,1)·(1+0,1)·(1+0,1)·(1+0,1) =

= 1000 грн · (1+0,1) ⁴ = 1000 грн · 1,4641 = 1464,1 грн.

Наприкінці четвертого року Ви одержите з банку на руки 1464,1 грн, після чого депозитний рахунок закривається і фінансова операція закінчується.

Отже, на початку першого року Ви вклали 1000 грн, а по закінченні чотирьох років Ви одержали фактично 1464,1 грн, тобто Вам повернули вкладені Вами 1000 грн і нарахували в кожному із чотирьох років проценти за складною схемою (нарахування процентів на процент), що в сумі склало 464,1 грн. процентів.

Розрахунок за механізмом складного нарахування процентів може мати інші назви-синоніми: такі як «нарахування процентів на проценти», «нарощення по складній процентній ставці», «нарахування складних процентів», «складна нарощена вартість», «складні проценти», «складна позика», будь-які інші.

Механізм нарахування складних процентів має послідовно змінну базу для розрахунку. Застосування змінної бази означає, що в наступному періоді за базу береться сума, отримана в попередньому періоді нарахування.

Процедура приєднання нарахованих процентів до попередньої суми може називатися їх реінвестуваннямабо капіталізацією.

Нарощення з використанням механізму складного нарахування процентів може мати назву ─ компаундінг або компандування (англ. compound), або мультиплікація.

У Модельній задачі 2 вкладені Вами на депозит 1000 грн – це PV, отримані Вами фактично 1464,1 грн – це FV,процентна ставка дорівнює 10% річних – це i, кількість разів (кількість періодів) нарахування процентів – це n.

З аналізу етапів Модельної задачі 2 можемо записати формулу складного нарахування процентів:

FV = PV ·(1 + і) 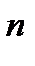, (2.10)

де FV – майбутня вартість у грошових одиницях (докладніше дивися початок підрозділу 1.6);

PV – початкова вартість у грошових одиницях (докладніше дивися початок підрозділу 1.6);

i– процентна ставка у кожному з періодів нарахування процентів n (але у формулі (2.10) процентна ставка i стає показником, що не має розмірності, тобто у формулі показник i використовується не у відсотках, а в частках, в долях, «як темп»);

n – кількість періодів нарахування процентів впродовж часу (строку) застосування ставки і; також, у кожному з цих періодів процентні ставки рівні між собою.

Показник (1+ і ·n) у формулі (2.2) та показник (1+ і) 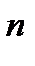із формули (2.10) називаються в деяких українських навчальних виданнях мультиплікуючими множниками. В інших джерелах їх називають коефіцієнтами або множниками нарощення. Їх чисельні показники для різних зна­чень ставки і і числа періодів п табульовані (заздалегідь розраховані) і приводяться в так званих фінансових таблицях. Існують множники механізмів простого і склад-ного нарахування процентів. Про множник нарощення простих процентів вже мова йшла ─ формула (2.3). Показник (1+ і) 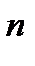, на відміну від 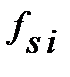, по суті є множником нарощення за складними процентами, або англ. ─ compound interest factor, звідки і походить позначка множника ─ 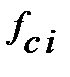. Через множник складного нарощення формулу (2.10) можна переписати у вигляді:

FV = PV · 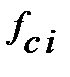. (2.11)

Після цього досить лише виписати з фінансової таблиці значення множника і підставити у формулу (2.11).

Мультиплікуючий (мультиплікативний) множник при будь-якому механізмі нара­хування процентів показує, у скільки разів збільшується початкова сума грошей при заданих процентній ставці і і кількості періодів нарощення процентів п. До сучасного широкого впровадження комп’ютерів і під час відсутності руч­них калькуляторів таблиці цих множників користували­ся широкою популярністю у фінансових установах. Тепер необхідність у них практично відпала.

Але, використання множників може стати в пригоді при записі формули у випадку, якщо механізм нарахування процентів змінюється впродовж строку фінансової опера-ції, також, змінюється процентна ставка і, також, зміню-ється період нарахування процентів. В такому випадку треба визначити свої множники нарощення 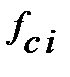, або 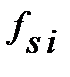на які потрібно помножити все, що отримано на поперед-ньому етапі. У підсумку, формула для визначення нароще-ної суми при будь-якій зміні способів нарахування процен-тів, процентних ставок і періодів нарахування, приймає вигляд:

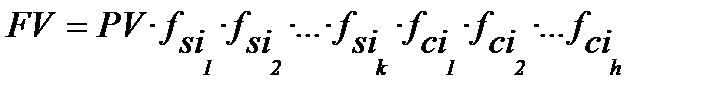. (2.12)

На практиці у фінансових обчисленнях в основному використовують формулу (2.10), а не (2.12).

На відміну від формули простого нарахування про-центів (2.2), яка є прийнятною для всіх варіантів співвідно-шення між періодом нарахування процентів і строком, формула (2.10) відображає виключно тільки 2-й варіант співвідношення між періодом нарахування процента і строком (див. стор. 51), а саме, що період нарахування процента менше за строк і при цьому тривалість періоду кратна строку, тобто строк має цілу кількість періодів.

При застосуванні механізму складного нарахування процентів за 3-им та 4-им варіантами (див. стор. 51), тобто, коли n має цілу і дробову частини, або тільки дробову, в цих випадках використовуються формули не у вигляді (2.10), а інші формули (див. пункти 2.2.2 та 2.2.3).

В Модельній задачі 2 період нарахування процентів ─ рік, строк ─ чотири роки, кількість періодів нарахування процентів (n) дорівнює цілій кількості періодів ─ чотирьом. Отже, можемо використати формулу (2.10) в розв’язуванні Модельної задачі 2.

Використовуючи (2.10), розв’язання Модельної задачі 2 приймає лаконічний вигляд:

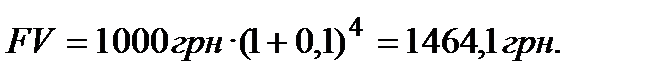
Відповідь:вМодельній задачі 2 фактична загальна сума грошей, що Ви одержите по закінченні чотирьох років будеFV = 1464,1 грн.

Формулу (2.10) використовують тоді, коли:

─ періоди нарахування процентів (n) рівні між собою;

─ в кожному періоді нарахування процентів (n) процентні ставки (і) рівні між собою (постійні ставки).

Коли процентні ставки в кожному з періодів нарахування різняться, а періоди нарахування процентів

згруповані за ознакою рівності між собою ( 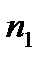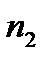… 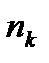), тобто, якщо процентна ставка перемінна, а саме:

─ протягом 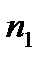періодів процентна ставка дорівнює ,

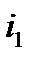─ протягом 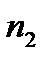періодів процентна ставка дорівнює ,

……………………………………………………………

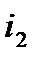─ протягом 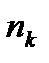періодів процентна ставка дорівнює ,

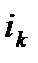то формула складного нарахування процентів приймає вигляд:

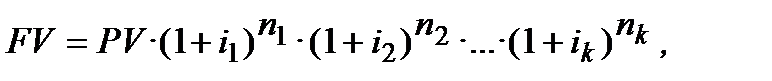(2.13)

де 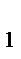і 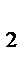, і ,…і ─ процентні ставки за періоди 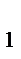n , n 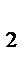, … …, n 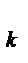,відповідно.

_Приклад 2.2___________________________________

Задача.

Підприємство одержало кредит в сумі 100 млн грн строком на 6 років за схемою нарахування складних процентів на наступних умовах :

─ у перший рік процентна ставка складає 10%;

─ для другого і третього року передбачена надбавка до ставки в розмірі 2%;

─ для четвертого року і наступного років надбавка до ставки третього року ─ 3%. Визначити суму боргу наприкінці строку позики.

Читайте також:

1. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
2. Абсолютний фагоцитоз або елімінуюча здатність крові (ЕЗК) — це кількість фагоцитованих мікробних клітин лейкоцитами 1 мкл крові.
3. Амортизація основних фондів підприємства. Методи нарахування амортизації
4. Амортизація основних фондів підприємства. Методи нарахування амортизації.
5. Амортизація основних фондів, методи її нарахування.
6. Амортизація. Методи нарахування амортизації.
7. Ануїтети з безперервним нарахуванням процентів
8. Ануїтети з виплатами в середині періодів
9. Безсполучникове складне речення
10. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
11. Бухгалтерський облік номіналу депозиту та нарахування процентів за депозитом
12. В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.

Переглядів: 552