• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Складне нарахування, яке має дробову кількість періодів нарахування процентів.

Розглядаємо варіант 4-й (див. стор. 51) коли період нарахування процента більше за строк фінансової операції.

Вже було доведено, щовипадок, коли у формулі (2.15) в «частині не повного періоду нарахування застосовують механізм складних процентів», то це не відповідає практичним реальностям фінансових розрахун-ків. У формулі (2.15) для множника за неповний період нарахування існує лише один спосіб розрахунку, ─ простий, що має вигляд (1+f·i) (див. стор. 98). Розглянемо випадок при застосуванні формули (2.15) коли k = 0, а f є дробовим числом. В цій формулі k виконує функції показнику ступеню (на відміну від f, який не працює як показник ступеню). Формула (2.15) стає такою:

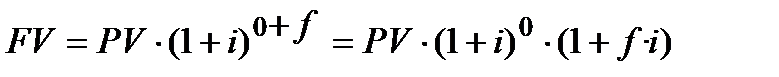. (2.15.1)

Математика підказує, що завжди будь-яке число або його показник в нульовому ступені дорівнює одиниці.

З фінансової тачки зору показник ступеню «0» означає що нарахування процентів не проводилося.

Таким чином, формула (2.15.1) перетворюється у наступну формулу ─ (2.15.2):

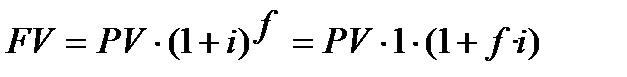. (2.15.2)

Отже, маємо, що 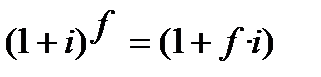, і таке рівняння у фінансах має місце завжди.

Варіант, що розглядається в цьому пункті (п. 2.2.3) і є випадком, коли період нарахування не повний, тобто дробовий і це в той же час означає, що період всього один.

Механізм складного нарахування процентів є механізмом зростання суми з попереднього періоду за наявності наступного, тобто періодів нарахування повинно бути декілька (обов’язково два і більше), тоді і тільки тоді може йти мова про застосування механізму складного нарахування процентів. Але, якщо період нарахування всього один, то зрозуміло, що нема на чому застосовувати механізм складного нарахування процентів. Саме тому, коли період нарахування процентів більший за строк операції, нарахування процентів завжди просте, складному нарахуванню нема на чому застосовувати свій механізм.

Читайте також:

1. Ni - загальна кількість періодів, протягом яких діє процентна ставка ri.
2. Абсолютний фагоцитоз або елімінуюча здатність крові (ЕЗК) — це кількість фагоцитованих мікробних клітин лейкоцитами 1 мкл крові.
3. Амортизація основних фондів підприємства. Методи нарахування амортизації
4. Амортизація основних фондів підприємства. Методи нарахування амортизації.
5. Амортизація основних фондів, методи її нарахування.
6. Амортизація. Методи нарахування амортизації.
7. Ануїтети з безперервним нарахуванням процентів
8. Ануїтети з виплатами в середині періодів
9. Безсполучникове складне речення
10. Біомаса - Кількість живої речовини на одиниці площі чи об'єму місцеперебування в момент спостереження. Визначається сумою біомаси усіх популяцій, що населяють дану екосистему.
11. Бухгалтерський облік номіналу депозиту та нарахування процентів за депозитом
12. В межах наукового підходу існує велика кількість концепцій, але найбільш переконлива – еволюційна теорія.

Переглядів: 358