• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

а ) PV = 400 тис. грн, n = 3, d=0,09.

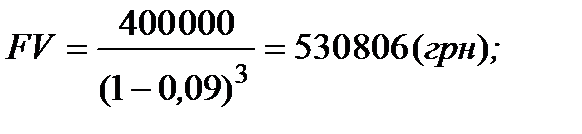
б ) PV = 400 тис. грн, n = 3·2=6, d=0,09/2.

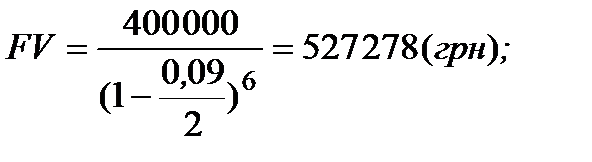
в ) PV = 400 тис. грн, n = 3·12=36, d=0,09/12.

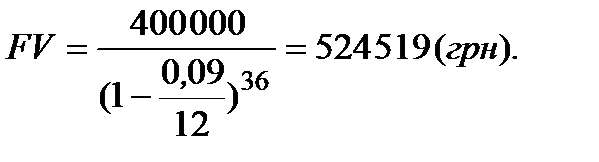
За допомогою Приклада 5.3 звернемо увагу на таку особливість. Якби нарощення складними процентами здійснювалось за допомогою процентної ставки (наприклад і = 9%), то для варіантів а), б), в) одержали б за формулою (2.10) відповідно значення: 518 012 грн, 520 904 грн, 523 458 грн, тобто, при зростанні в межах року кількості періодів нарахування процентів розмір нарощеної суми збільшується. Нарощення за складною обліковою ставкою дає протилежну тенденцію. При зростанні в межах року кількості періодів нарахування процентів при застосуванні складної облікової ставки нарощена сума зменшується. Якщо кількість періодів нарахування в межах року збільшувати, то різниця між майбутніми нарощеними сумами, розрахованими за складними процентними ставками і складними обліковими ставками, зменшується. Так, наприклад, якщо нарахування процентів буде щоденним, то застосування облікової ставки дає результат FV = 524 003 грн,а при такій же чисельно процентній ставці FV = 523 968 грн, і різниця між цими сумами дорівнює всього 35 грн.

Ще одна особливість. Якщо облікова і процентна ставки чисельно рівні між собою, то складне нарощення за обліковою ставкою (5.6) є більш швидким (що є вигідним для кредитора), чим нарощення за процентною ставкою (2.10) ( що вигідніше для боржника).

Як вже зазначалося, термінологічне різноманіття перерахунку вартостей можна пов’язати з англійським терміном compound, що означає складний механізм нарахування, і саме нарахування, як нарощення, як збільшення, як перерахування сьогоднішньої вартості в майбутню вартість. При використанні облікової ставки може використовуватись термін ─ обліковий компаундінг, або облікове компандування, але ні в якому разі ─ компандування. Термін компандування без пояснення яке: процентне чи облікове, означає процентне компандування.

Формула (5.6) відображає розрахунок нарощеної суми (FV) з використанням складної облікової ставки, а розрахунок безпосередньо нарощення, або прирощення, тобто ─ проценту, позначимо 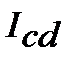(Interest of compound discount) і можемо знайти за формулою:

(5.7)

Формула (5.7) має ще іншу модифікацію свого запису:

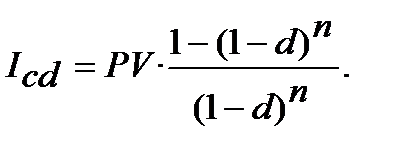(5.7.1)

Формула (5.7) (5.7.1) дає можливість розраховувати при складному обліковому нарощенні процент (процент складного облікового нарощення) від PV не обчислюючи FV.

Показник 1/(1─d) є множником складного обліко-вого нарощення. Цей множник показує зростання капіталу PV за кількість періодів n при застосуванні складної облікової ставки d.

При PV = 1, n = 1 з формули (5.6) також, як і з формули (5.3) виходить, що;

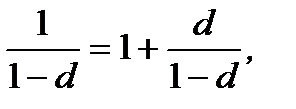(5.4)

тобто, коефіцієнт нарощення 1/(1 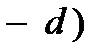є в майбутньому сумою, наприклад, 1 грн, разом з нарахованим процентом за один рік.

Розглянемо випадок, коли облікові ставки в періодах нарахування «плаваючі», тобто ─ різні.Якщо в періодах нарахування процентів 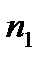, 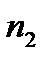… 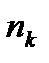облікові ставки відповідно дорівнюють 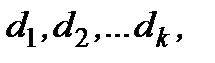при нарощенні складними процентами майбутня сума за строк 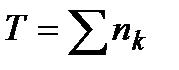(вимір періодів 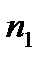, 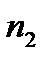… 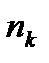в єдиних одиницях часу) розраховується за формулою:

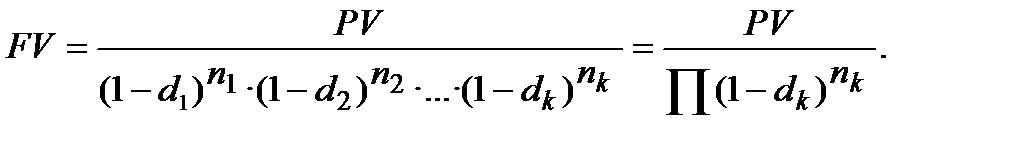(5.8)

У формулі (5.8) показник 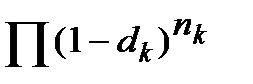можемо перерахувати в еквівалентний йому показник і знайти одну облікову ставку (позначимо її ─ 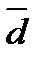) еквівалентну декільком обліковим ставкам :

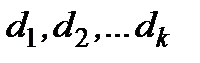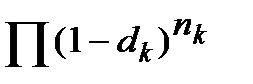
. (5.9)

Розв’язуючи рівняння (5.9) відносно 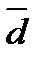маємо:

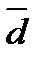= 1 ─ [ 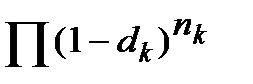] 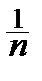, тоді (5.5) приймає вигляд 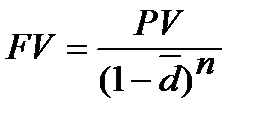. Таким чином, за n періодів нарахуваннявпродовж строку Т можемо встановити та використовувати замість плаваючих облікових ставок облікову ставку 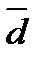, яка забезпечує такий же результат, і тому при розрахунку FV можемо використовувати формулу (5.6). Якщо d, тобто за весь строк Т встановлена одна постійна ставка, то з (5.8) одержуємо (5.6).

Формулою (5.8) також можна користуватися і у випадку, коли періоди нарахування надані в різних одиницях часу при умові відповідності їх розмірностей з розмірами відповідних облікових ставок.

При складному обліковому нарощенні за цілу й дробову кількість періодів нарахування процентів застосо-вується формула змішаного обліку процентів (4.7). Від формули (4.7) формула складного облікового нарощення приймає вигляд:

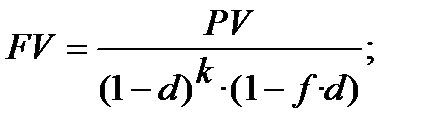(5.10)

деFV, PV, d – мають зміст той же, що й у формулах (4.1), (4.3), (4.5), (5.1), (5.6);

k– ціла частина кількості періодів нарахування;

f – дробова частина кількості періодів нарахування процентів.

При складному обліковому нарощенні, коликількість періодів нарахування дробовавикористовують формулу (4.3).

Читайте також:

1. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
2. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
3. Розв’язання.
4. Розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.

Переглядів: 814