• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язання.

Витрати підприємця на обслуговування позики (процент за позику) можуть бути визначеними за допомогою розрахунку ефективної процентної ставки ─ чим вона вище, тим більше рівень витрат.

За формулою (9.12):

─ варіант а):

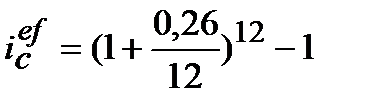=0,2933;

─ варіант а):

=0,2882.

Таким чином, варіант б) є більш прийнятним для підприємця.

За допомогою квадратів ставок ефективності (Рис.9.1) можливе вирішення оберненої задачі: ─ розрахунок номінальної ставки з m–разовим нарахуванням процентів, якщо наперед відома ефективна ставка.

Треба взяти один з множників, що надано в квадраті множників номінальних ставок і дорівняти окремим рівнянням до кожного множника, що представлені у квадраті множників ефективних ставок. Потім, кожне рівняння розв’язати відносно номінальної ставки. Очевидно, що також, таких формул розрахунку номінальних ставок по співвідношенню до ефективних має бути шістнадцять, але дві з них вже відомі, це формули (9.7), (9.17). Інші чотирнадцять формул одержуємо з не складних перетворень, описаних на початку цього абзацу.

1. Номінальну складну процентну ставку 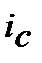, що відповідає ефективній простій процентній ставці 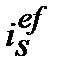знаходимо з дорівнювання множників

= :

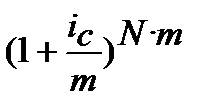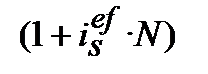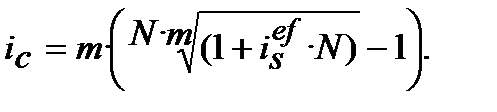(9.23)

2. Номінальну просту облікову ставку 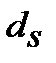, що відповідає ефективній простій процентній ставці 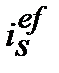знаходимо з дорівнювання множників

= :

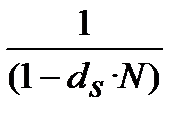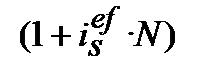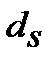= (9.24)

3. Номінальну складну облікову ставку , що відповідає ефективній простій процентній ставці 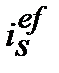знаходимо з дорівнювання множників

= :

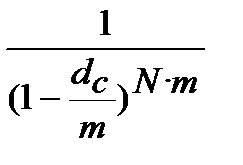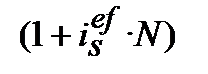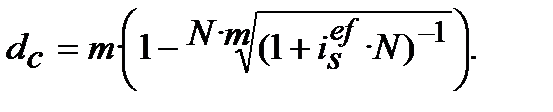(9.25)

4. Номінальну просту процентну ставку 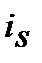, що відповідає ефективній складній процентній ставці і 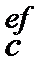знаходимо з дорівнювання множників

= :

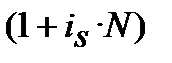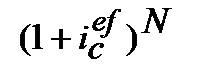(9.26)

5. Номінальну складну процентну ставку , що відповідає ефективній складній процентній ставці і 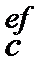знаходимо з дорівнювання множників

= :

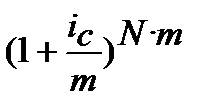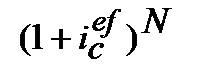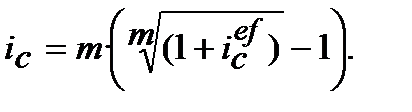(9.27)

6. Номінальну просту облікову ставку 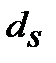, що відповідає ефективній складній процентній ставці і 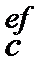знаходимо з дорівнювання множників

= :

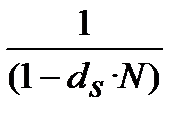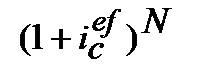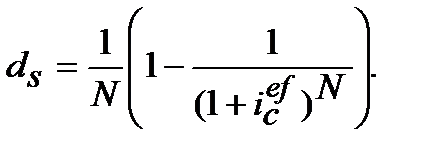(9.28)

7. Номінальну складну облікову ставку 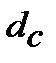, що відповідає ефективній складній процентній ставці і 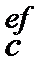знаходимо з дорівнювання множників

= :

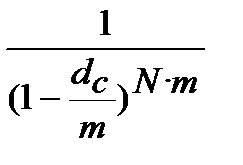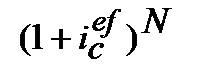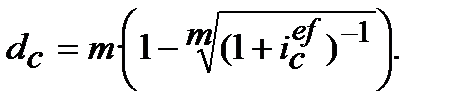(9.29)

8. Номінальну просту процентну ставку 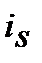, що відповідає ефективній простій обліковій ставці 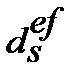знаходимо з дорівнювання множників

= :

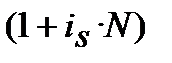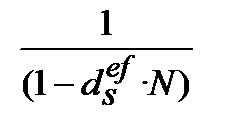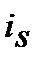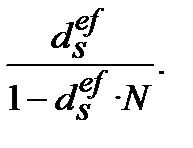= (9.30)

9. Номінальну складну процентну ставку 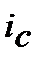, що відповідає ефективній простій обліковій ставці 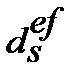знаходимо з дорівнювання множників

= :

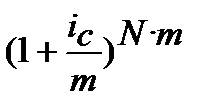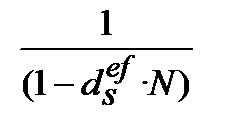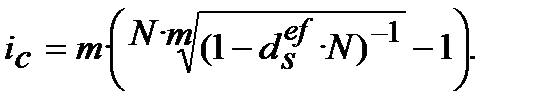(9.31)

10. Номінальну складну облікову ставку 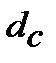, що відповідає ефективній простій обліковій ставці 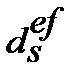знаходимо з дорівнювання множникі

= :

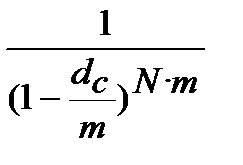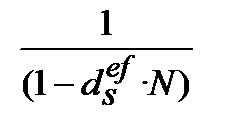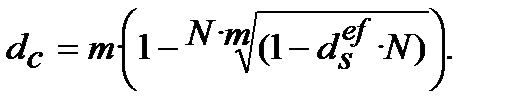(9.32)

11. Номінальну просту процентну ставку , що відповідає ефективній складній обліковій ставці 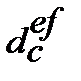знаходимо з дорівнювання множників

= :

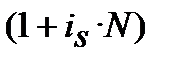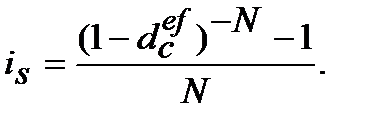(9.33)

12. Номінальну складну процентну ставку 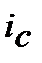, що відповідає ефективній складній обліковій ставці 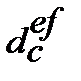знаходимо з дорівнювання множників

= :

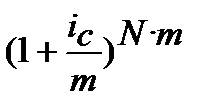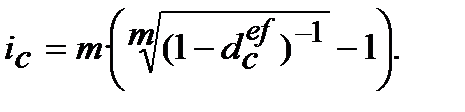(9.34)

13. Номінальну просту облікову ставку 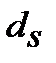, що відповідає ефективній складній обліковій ставці 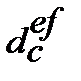знаходимо з дорівнювання множників

= :

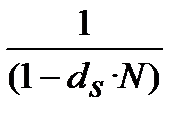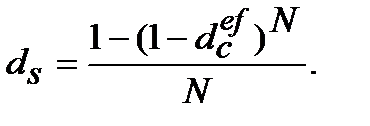(9.35)

14. Номінальну складну облікову ставку 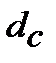, що відповідає ефективній складній обліковій ставці 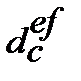знаходимо з дорівнювання множників

= :

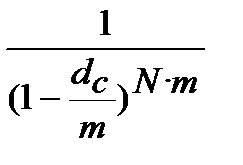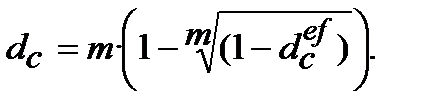(9.36)

Цікавим є ще один момент еквівалентності номінальних ставок. Якщо дві номінальні (річні) ставки процента визначаються через одну і ту ж ефективну ставку, то вони є еквівалентними. З цього визначення випливає, що еквівалентні, наприклад, складні процентні ставки 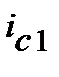та 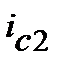задовольняють рівнянню, (див. (9.12)):

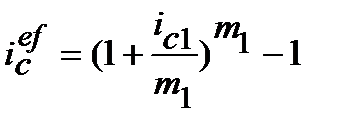
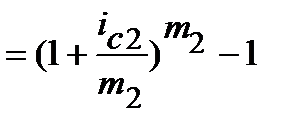; (9.37)

з якого виникає рівняння еквівалентності ставок при різних m-разових нарахуваннях процентів за рік але, обов’язково за умови рівності строків Т, або, що одне і теж, за умови рівності N. Отже, еквівалентна заміна номінальної ставки має місце в тому випадку, коли виконується рівняння:

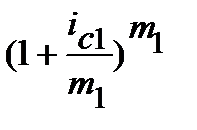
(9.38)

Якщо у рівнянні (9.38) m має лише цілі значення, то можемо одержати дві формули еквівалентності:

(9.39)

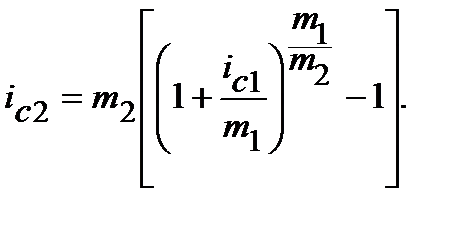(9.40)

_Приклад 9.3__________________________________

Читайте також:

1. Міжнаціональні відносини і причини виникнення міжнаціональних конфліктів, шляхи їх розв’язання. Міжконфесійні стосунки та їх вплив на життя в полікультурному суспільстві
2. Поняття біосфери та ноосфери. Поняття екології. Основні завдання соціальної екології. Сучасні екологічні проблеми, причини їх виникнення та розв’язання.
3. Розв’язання.
4. Розв’язання.
5. Розв’язання.
6. Розв’язання.
7. Розв’язання.
8. Розв’язання.
9. Розв’язання.
10. Розв’язання.
11. Розв’язання.

Переглядів: 565