Розв’язання задачі

FV = 500·(1+0,2)³ + 500·(1+0,2)^2,5 + 500·(1+0,2)² + + 500·(1+0,2)^1,5 + 500·(1+0,2)¹ 500·(1+0,2)^0,5 = 500·(1+0,2)³ + 500·(1+0,2)²·(1+0,5·0,2) + 500·(1+0,2)² + 500·(1+0,2)¹· ·(1+0,5·0,2) + 500·(1+0,2)¹ + 500·(1+0,2)⁰·(1+0,5·0,2) = = 4186 грн.

Відповідь: майбутня вартість ануїтету пренумерандо 500 грн., вкладених кожні півроку впродовж 3-х років при ставці 20% дорівнює 4186 грн.

ЗАПАМ'ЯТАЙТЕ:в задачі прикладу 12.1 надход-ження внесків – КОЖНІ ПІВРОКУ, а нарахування процентів – ЩОРОКУ. Будь ласка, надалі, не плутайте вирази:ПЕРІОД НАРАХУВАННЯ ПРОЦЕНТІВ та ПЕРІОД ВКЛАДАННЯ ВНЕСКІВ.

Розрахунок показників FV і PV грошових потоків, у тому числі фінансової ренти й ануїтетів, проводиться за формулами, що носять загальний характер:

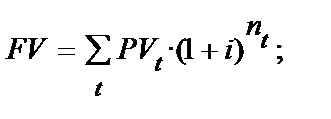(12.1)

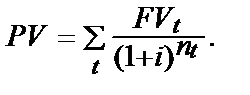(12.2)

де PV_t – сума надходження або видатку (вкладання на рахунок або вилучення з рахунку) t – го надходження (вилучення)

FV_t - сума надходження або видатку (вкладання на рахунок або вилучення з рахунку) t – го надходження (вилучення)

t – порядковий номер надходження (вилучення) грошової суми PV_t або FV_t грошового потоку

i – процентна ставка у кожному з періодів нарахування процентів n_t;

n_t – кількість періодів нарахування процентів, у кожному з яких процентна ставка дорівнює iдля відповідногоPV_tабо FV_t.

ЗАПАМ'ЯТАЙТЕ: у формулах (12.1) і (12.2) ЗНАК СУМИΣМАЄ АЛГЕБРАЇЧНЕ ЗНАЧЕННЯ, тобто, якщо внески, надходження на рахунок прийняти зі знаком «+», то вилучення, зняття з рахунку приймається зі знаком «–».

Уявлення про грошові потоки в їх різноманітності, дає їх описання та класифікація. За основу опису та класифікації візьмемо Долінського [6, стор. 32-33] з деякими нашими змінами та доповненнями.

Кожний грошовий потік описується такими параметрами:

─ член грошового потоку ─ величина кожного окремого платежу;

─ період грошового потоку ─ проміжок часу між двома послідовними платежами;

─ строк грошового потоку ─ час від початку першого періоду грошового потоку до кінця останнього періоду;

─ ставка проценту (ставка доходності) ─ використовується у разі нарощення або дисконтування платежів, з яких складається грошовий потік;

─ механізм нарахування процентів (простий, складний чи безперервний);

Для окремих видів грошових потоків розраховуються або вказуються додаткові параметри:

─ кількість платежів у році;

─ частота нарахування процентів тощо.

Класифікацію видів грошових потоків наведено в табл. 12.1

Таблиця 12.1

Ознака класифікації	Вид грошового потоку
Періодичність платежів	Річні (платіж один раз за рік); р-термінові (р платежів за рік)
Частота платежів	Дискретні; Безперервні
Проміжки між плате- жами (для дискретних платежів)	Рівні між собою (регулярні) ─ це ознака як для ренти так і для ануїтету; Не рівні між собою (нерегулярні)
Величина членів грошового потоку	Постійні (з однаковими членами) ─ це одна із ознак ануїтету; Змінні (з різними членами) ─ це одна із ознак фінансової ренти
Кількість членів, платежів	Обмежені (з кінцевою кількістю членів, платежів); Необмежені (вічні)
Обов’язковість платежу	Умовні (кількість членів наперед не відома, оплачуються згідно з умовою); Безумовні, правильні (обов’язково оплачуються)
Момент платежу	Звичайні ─ постнумерандо (платежі в кінці періодів платежів); Авансові ─ пренумерандо (платежі на початку періодів платежів)

Узагальнюючі показники для будь-яких видів грошових потоків ─ це нарощена (майбутня) вартість і теперішня (поточна) величина грошового потоку.

Нарощена сума грошового потоку (FV) ─ це сума всіх членів грошового потоку з нарахованими на них процентами на кінець строку.

Теперішня величина грошового потоку (PV) ─ це сума всіх членів грошового потоку, дисконтованих на початок її строку. Цю величину можуть називати капіталізованою ціною ренти (ануїтету).

Крім вказаних показників розглянемо методи розрахунку строку потоку і розміру періодичного платежу.

Надалі будемо користуватися позначками:

Р ─ сума платежу, внеску, плати, сума надходжень або виплат (від англ. ─ pay, payment);

Т ─ строк грошового потоку;

k ─ кількість платежів (виплат) Р впродовж строку Т;

р ─ кількість платежів Р у році;

і ─ процентна ставка;

n ─ кількість періодів нарахування процентів;

m ─ кількість нарахувань процентів у році;

N ─ кількість років.

У навчальній літературі, в якій автори розглядають грошові потоки і формулюють їх визначення як фінансову ренту, при виведенні формул розрахунку завжди надають формули ануїтетів. Автори (наприклад ─ Четыркин [15], Долінський [6], Мелкумов [11]) в назвах пунктів підручників повідомляють про розрахунок рент, а в тексті пунктів мова йде про ануїтети. Такий факт намагалася пояснити Машина [9, стор.54] «Вивести зручні формули для розрахунків можна тільки для потоків з постійними членами і конкретними умовами нарахування процентів.» Потік «…з постійними членами…» ─ це одна із ознак ануїтету. Про іншу ознаку ануїтету Машина у наведеному поясненні не згадує і тому більш повним буде таке пояснення. «Вивести зручні формули для розрахунків можна тільки для потоків з постійними розмірами платежів (виплат) і рівними проміжками часу між ними за наявності інших конкретних умов нарахування процентів.» Іншими словами, ─ при розрахунку грошових потоків виводимо формули для ануїтетів.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Стратегія розв’язання	\|	Майбутня та теперішня вартості звичайного ануїтету (ануїтету постнумерандо)

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.