
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Розв’язування задачі
Нарощена сума за складним механізмом нарахування процентів дорівнює:
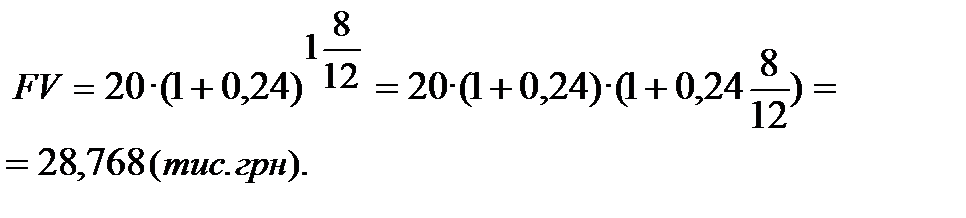
Розмір щомісячного платежу (за механізмом «add-on interest»):
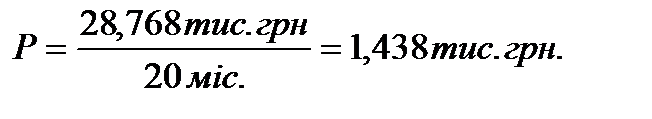
Якщо буде застосовано простий механізмом нарахування процентів, то нарощена сума дорівнює:
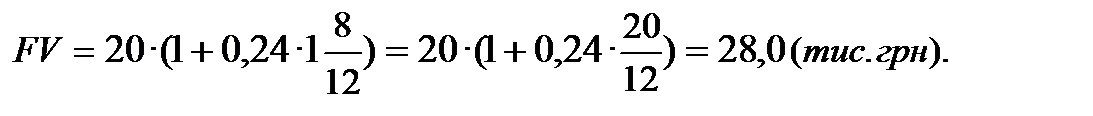 В цьому випадку розмір щомісячного платежу (за механізмом «add-on interest»):
В цьому випадку розмір щомісячного платежу (за механізмом «add-on interest»):
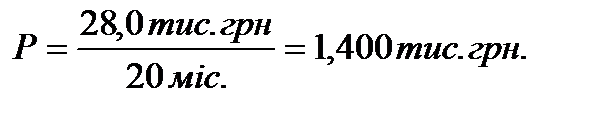
Таким чином, розмір щомісячного платежу за механізмом «add-on interest» може коливатися в межах від 1400 до 1438 грн.
Фактичний розмір щомісячного платежу по кредиту розраховуємо за допомогою формули (12.9):
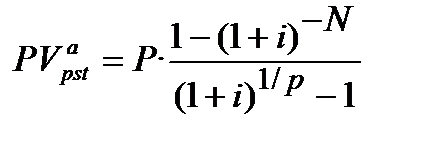 (12.9)
(12.9)
за якою після підрахунків Р дорівнює 1200 грн.
Висновок: понад 200 грн щомісячно позичальник «переплачує» за взятий кредит.
При погашенні споживчого кредиту рівними платежами може виникнути потреба у визначенні частини в кожній виплаті, яка іде на погашення основного боргу і частини в тій же виплаті, яка іде на погашення нарахованих процентів. Для складення такого плану виплат можна скористатися «правилом 78», суть якого в наступному.
Знаходимо суму порядкових номерів всіх платежів. Наприклад, якщо таких платежів 12, тоді 1+2+3+…+12=78 (це, доречи, і дало назву правила, тому що в році 12 місяців, а платежі досить часто здійснюються щомісячно). Згідно «правила 78» частина від першого платежу у розмірі 12/78 від загальної нарахованої суми процентів (тобто, 12/78  І) піде на виплату процентів, а частина, що залишається у складі першого платежу ─ (Р ─ 12/78
І) піде на виплату процентів, а частина, що залишається у складі першого платежу ─ (Р ─ 12/78  І) «піде» в рахунок виплат основного боргу. У складі другого платежу на виплату процентів «піде» сума в розмірі 11/78 від загального нарахованого розміру процентів (тобто, 11/78
І) «піде» в рахунок виплат основного боргу. У складі другого платежу на виплату процентів «піде» сума в розмірі 11/78 від загального нарахованого розміру процентів (тобто, 11/78  І), а частина платежу, що залишилась (Р ─ 11/78
І), а частина платежу, що залишилась (Р ─ 11/78  І) є частиною виплати основного боргу у складі другого платежу. Для третього платежу треба взяти дріб 10/78 і провести далі розрахунки за попереднім механізмом.
І) є частиною виплати основного боргу у складі другого платежу. Для третього платежу треба взяти дріб 10/78 і провести далі розрахунки за попереднім механізмом.
У загальному випадку, якщо є k запланованих платежів, то при введенні позначки К як суми платежів:
К=1+2+…+k = 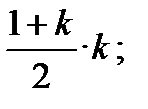
при використанні «привила 78» треба послідовно брати дроби 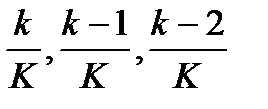 і так до
і так до 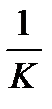 включно. Зазначимо, що сума всіх цих дробів дорівнює одиниці, тобто
включно. Зазначимо, що сума всіх цих дробів дорівнює одиниці, тобто 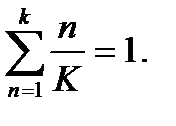
При застосуванні «правила 78» розмір процентів у складі кожного наступного платежу зменшується. Схема спадного розміру суми процентів у складі платежів по погашенню кредиту має дві сторони. По-перше, вона відповідає суті кредитних операцій: бо з кожним платежем відбувається погашення основної суми боргу, тому і сума процентів, яка нараховується на зменшений залишок непоганеного боргу, відповідно зменшується. По-друге, зменшення суми проценту в кожному з платежів страхує кредитора на випадок дострокового погашення боргу, якщо це передбачено кредитним договором. Вочевидь, в кредитному договорі можуть бути передбачені будь-які схеми застосування питомих коефіцієнтів розподілення загальної суми процентів впродовж періоду кредитування. Загалом, при складанні плану погашення кредиту можна використовувати будь-яку послідовність дробів (зокрема ─ зростаючу), аби сума цих дробів дорівнювала одиниці.
Складемо план погашення кредиту за умов попереднього прикладу 13.12.
_Приклад 13.12_(продовження) ________________
Заплановано k =20 платежів. Тоді:
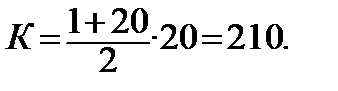
В частині першого платежу розмір процентів дорівнює 20/210 від загальної суми нарахованих процентів, що складає 8,000 тис. грн  20/210 = 0,762 тис. грн. Отже, в першому місяці частина основного боргу погашається в розмірі 1,400 ─ 0,762 = 0,638 (тис. грн). На початок наступного місяця одержуємо залишок основного боргу, який дорівнює 20,0 ─ 0,638 = 19,362 (тис. грн).
20/210 = 0,762 тис. грн. Отже, в першому місяці частина основного боргу погашається в розмірі 1,400 ─ 0,762 = 0,638 (тис. грн). На початок наступного місяця одержуємо залишок основного боргу, який дорівнює 20,0 ─ 0,638 = 19,362 (тис. грн).
В наступному другому місяці розмір процентів у складі платежу дорівнює 19/210 від суми нарахованих процентів і складає 8 тис. грн  19/210 = 0,724 тис. грн. Тоді, в другому місяці, частина основного боргу погашається в розмірі 1,400 ─ 0,724 = 0,676 (тис. грн). На початок наступного місяця одержуємо залишок основного боргу, який дорівнює 19,362 ─ 0,676 = 18,686 (тис. грн). Результати наступних розрахунків надані в табл. 13.20.
19/210 = 0,724 тис. грн. Тоді, в другому місяці, частина основного боргу погашається в розмірі 1,400 ─ 0,724 = 0,676 (тис. грн). На початок наступного місяця одержуємо залишок основного боргу, який дорівнює 19,362 ─ 0,676 = 18,686 (тис. грн). Результати наступних розрахунків надані в табл. 13.20.
Таблиця 13.20.
План погашення кредиту в сумі 20 тис. грн рівними щомісячними платежами в розмірі 1400 грн/міс., розрахований за допомогою «правила 78», тис. грн.
| Місяць | Дріб | Погашення загального розміру нарахованих процентів | Залишок основного боргу на початок місяця | Погашення основного боргу |
| 1 | 2 | 3 | 4 | 5 |
| 20/210 | 0,762 | 20,000 | 0,638 | |
| 19/210 | 0,724 | 19,362 | 0,676 | |
| 18/210 | 0,686 | 18,686 | 0,714 | |
| 17/210 | 0,648 | 17,972 | 0,752 | |
| 16/210 | 0,610 | 17,220 | 0,790 | |
| 15/210 | 0,571 | 16,430 | 0,829 | |
| 14/210 | 0,533 | 15,601 | 0,867 | |
| 13/210 | 0,495 | 14,734 | 0,905 | |
| 12/210 | 0,457 | 13,829 | 0,943 | |
| 11/210 | 0,419 | 12,886 | 0,981 | |
| 10/210 | 0,381 | 11,905 | 1,019 | |
| 9/210 | 0,343 | 10,886 | 1,057 | |
| 8/210 | 0,305 | 9,829 | 1,095 | |
| 7/210 | 0,267 | 8,734 | 1,133 | |
| 6/210 | 0,229 | 7,601 | 1,171 | |
| 5/210 | 0,190 | 6,430 | 1,210 | |
| 4/210 | 0,152 | 5,220 | 1,248 | |
| 3/210 | 0,114 | 3,972 | 1,286 | |
| 2/210 | 0,076 | 2,686 | 1,324 | |
| 1/210 | 0,038 | 1,362 | 1,362 | |
| Всього | 8,000 | 20,000 |
В табл. 13.20 останній рядок «Всього» служить для контролю наведених розрахунків: сума всіх показників третього стовпця повинна дорівнювати загальній сумі процентів, а сума п’ятого стовпця ─ сумі основному боргу (позиці). Окрім того, для кожного місяця сума у кожному рядку третього та п’ятого стовпців є фіксованою величиною та дорівнює розміру щомісячного платежу ─ 1400 грн.
За допомогою «правила 78» позичальник може розрахувати, яку суму в частині оплати процентів йому не треба віддавати у випадку повернення кредиту раніше встановленого строку (якщо така умова оговорена у договорі кредитування). Якщо було заплановано k платежів, а після m-го платежу було прийнято рішення повернути кредит, то суму процентів, що залишилася в кожному з (k ─ m) платежів, виплачувати не треба. Отже, не треба сплачувати суму (суму процентів), яка дорівнює 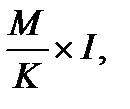 де М = 1+2 +…+ (k ─ m). Покажемо цей розрахунок на прикладі 13.12.
де М = 1+2 +…+ (k ─ m). Покажемо цей розрахунок на прикладі 13.12.
_Приклад 13.12_(продовження) _________________
На початку кредитної операції планувалося k=20 платежів, за яких К=210. Після восьми платежів прийнято рішення повернути частину основного боргу, що залишилась. Починаючи з одиниці знаходимо суму порядкових номерів платежів, що залишаються не сплаченими і знаходимо суму їх нових порядкових номерів, тобто, розраховуємо показник М.
М = 1+2+3+….+12= 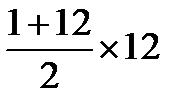 =78.
=78.
Тоді 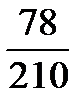 від загальної суми нарахованих процентів не треба сплачувати, тобто не треба сплачувати суму, що дорівнює
від загальної суми нарахованих процентів не треба сплачувати, тобто не треба сплачувати суму, що дорівнює 
Треба звернути увагу, що в попередніх розрахунках «правило 78» застосовувалось як механізм рознесення загальної суми процентів до складу рівних платежів, і саме такої суми процентів, розмір якої розрахований на взяту позику і є незмінним впродовж строку кредитування.
«Здирницький» характер розрахунку платежів по споживчого кредиту зникає, якщо застосовувати «правило 78» не до визначення частин від суми процентів по кредиту, яка розрахована на початку операції кредитування, а до основної суми по кредиту. Другий спосіб застосування «правила 78» полягає у вимозі, що основна сума поділяється на рівні частини, які виплачує боржник, і у факті, що процентні платежі розраховуються на залишок боргу і тому зменшуються у складі кожної виплати. Тобто, розмір кожної виплати зменшується за рахунок зменшення процентів у складі платежу.
Узагальнено такий розрахунок має таку побудову. Якщо платежі вносяться кожні l місяців, тобто, кожний рік 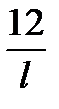 разів і всього кількість платежів за строк кредитної операції дорівнює:
разів і всього кількість платежів за строк кредитної операції дорівнює: 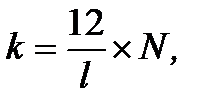 тоді у складі першого платежу нараховані проценти в сумі:
тоді у складі першого платежу нараховані проценти в сумі:
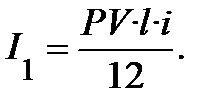
У наступному платежі проценти нараховуються на залишок позики, тобто, виплачена частина основної суми в розмірі  вилучається з розрахунку:
вилучається з розрахунку:

Таким же чином ведемо розрахунок процентів у складі третьої виплати:
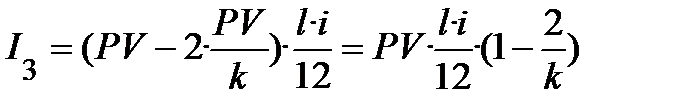
і так надалі, для інших за порядком платежів. Останній розрахунок має такий вигляд:

Загальний розмір процентів за користування кредитом дорівнює сумі процентних платежів, які розраховано попереднім способом:
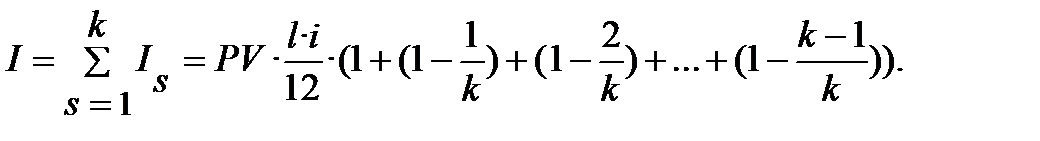 (13.23)
(13.23)
У формулі 13.23 в дужках ─ арифметична прогресія з першим членом, що дорівнює 1, та різницею ( 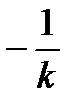 ), отже, одержуємо:
), отже, одержуємо:
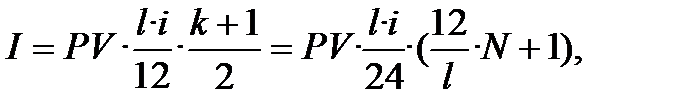 (13.24)
(13.24)
де 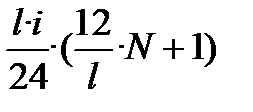 має назву процентного коефіцієнта, який відображує співвідношення між розміром процентного платежу і сумою кредиту (позики).
має назву процентного коефіцієнта, який відображує співвідношення між розміром процентного платежу і сумою кредиту (позики).
І лише тепер, коли за формулою 13.24 буде знайдена загальна сума процентів, є можливість розрахувати, якщо виникає потреба, платіж рівними частинами, який дорівнює:
 (13.25)
(13.25)
Рівні між собою платежі, розраховані за формулою 13.25, не будуть «здирницькими», а будуть відносно справедливими, звісно, якщо кредитна операція є також такою.
_Приклад 13.12_(продовження) _________________
За умов прикладу 13.12 скласти план погашення кредиту другим способом застосування «правила 78».
Як вже зазначалося раніше, щомісячний платіж є сумою яка складається з місячної частини основного боргу і процентів за відповідний місяць.
Кожного місяця сплачується частина основного боргу в розмірі: 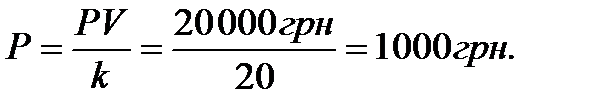
Проценти, які сплачуються в кожному місяці, розрахуємо за формулами, які враховують щомісячне зменшення боргу:
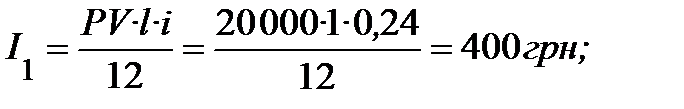
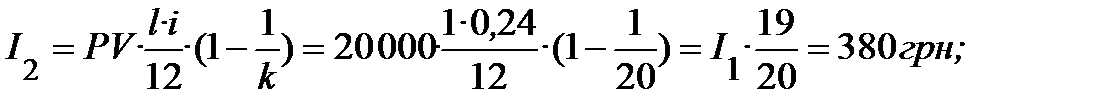
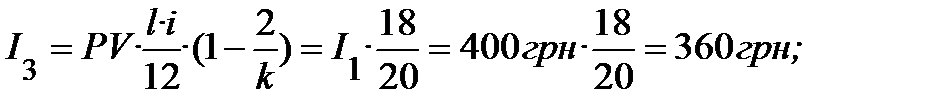
і так продовжити розрахунки процентів до двадцятого місяця включно.
Фактично, при розрахунку щомісячних процентів, розмір першого процентного платежу множимо послідовно на дроби  . Таким чином:
. Таким чином:
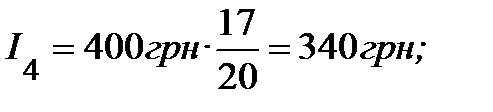

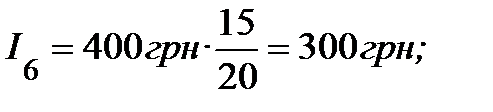
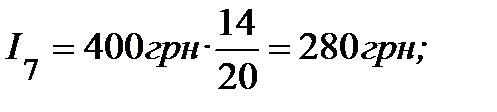
і так далі до І20 включно.
Отже, загальна сума процентів разом за 20 місяців складе:
І=400+380+360+340+320+300+280+260+240+220++200+180+160+140+120+100+80+60+40+20=4200 (грн).
Таку ж суму можна одержати і за розрахунком за формулою 13.24:
 Запишемо план погашення кредиту в табличній формі, табл. 13.21
Запишемо план погашення кредиту в табличній формі, табл. 13.21
Таблиця 13.21.
План погашення кредиту в сумі 20 тис. грн рівними щомісячними частинами основного боргу, та процентами, що зменшуються, розрахованих за допомогою «правила 78», грн.
| Місяць | Розмір щомісяч-ного платежу | Місячний розмір нарахованих процентів | Погашення основного боргу | Залишок основного боргу на початок місяця |
| 1 | 2 | 3 | 4 | 5 |
Продовження табл. 13.21
| 1 | 2 | 3 | 4 | 5 |
| Всього |
В табл. 13.21, також як і в табл. 13.20, останній рядок «Всього» є контролюючим показником.
За другим способом застосування «правила 78» загальний розмір виплат менше на 3800 грн, менше майже вдвічі, порівняно зі способом, який застосовувався першим у прикладі 13.12.
Якщо перейти до вимоги сплати кредиту рівними долями (в межах другого способу), то за формулою 13.25 знаходимо:
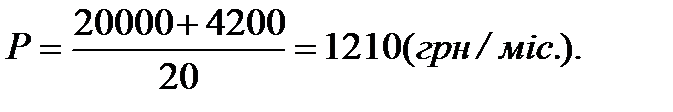
Читайте також:
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
- Аналіз інформації та постановка задачі дослідження
- Аналіз перед розв’язуванням задачі
- Аналіз перед розв’язуванням задачі
| <== попередня сторінка | | | наступна сторінка ==> |
| Здирницький» механізм погашення кредиту рівними сумами | | | Пільгове кредитування. |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |