Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Історична довідка

1. Криві і поверхні 2-го порядку у працях давньогрецьких математиків. Протягом всієї історії розвитку науки і техніки криві другого порядку незмінно привертали до себе увагу багатьох дослідників і вчених. З ними були знайомі ще давні греки.

Грецькі математики не знали ні методу координат, ні рівнянь, тим не менш всі властивості еліпса, гіперболи і параболи були їм добре відомі. Вони отримували і вивчали ці криві як плоскі перерізи конічної поверхні.

Першим у цьому був давньогрецький геометр Менехм (IV ст. до н.е.), який працював в Академії Платона. Саме йому приписується самостійне відкриття трьох видів конічних перерізів, які іноді і називають тріадою Менехма.

Вивчення еліпса, гіперболи і параболи Менехм проводив, розсікаючи поверхню конуса площиною, перпендикулярною до твірної. Але для отримання кожної з названих кривих йому доводилося брати різні конуси: для отримання еліпсу він брав конус з гострим кутом між протилежними твірними, для гіперболи – конус з тупим і для параболи – конус з прямим кутом.

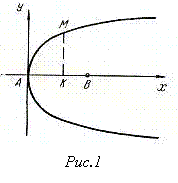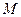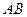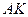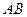Менехму вдалося отримати багато співвідношень, які виражають властивості кривих, які вивчаються. Так, наприклад, у випадку параболи йому вдалося довести, що квадрат, побудований на перпендикулярі , опущеному з будь-якої точки кривої на вісь симетрії , рівновеликий прямокутнику, сторони якого і , де 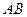– відрізок цілком певний для даної параболи (рис.1). Якщо виразити це співвідношення аналітично, то отримаємо рівняння .

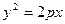Вказане рівняння замінює собою те рівняння параболи, яке ми записуємо у наш час, якщо за вісі координат приймаємо вісь симетрії параболи і пряму, їй перпендикулярну, яка проходить через вершину параболи. Прийнявши вісь абсцис за вісь , а вісь ординат за вісь , ми отримаємо рівняння , де 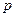– величина, стала для даної параболи.

Пізніше у III ст. до н.е. Архімед у своїй праці «Про коноїди і сфероїди» розглядає поверхні 2-го порядку. Коноїдами він називав тіла, отримані в результаті обертання параболічного чи гіперболічного сегмента навколо його осі, тобто тіла, які ми називаємо параболоїдами і гіперболоїдами.

До речі, найменування Архімеда було правильнішим, ніж прийняте нами, так як «параболоїд» значить «схожий на параболу», а «коноїд» – «схожий на конус». Наш термін неправильний, так як неможна говорити про схожість тіла і лінії; між тим термін Архімеда вказує, що мова йде про тіло, схоже на конус.

Подальшим вивченням конічних перерізів займався молодший сучасник Архімеда з міста Пергі – Аполлоній Пергський (бл.260–170 до н.е.). Його найвизначніша праця «Коніка» («Конусні») присвячена саме конічним перерізам, або кривим другого порядку.

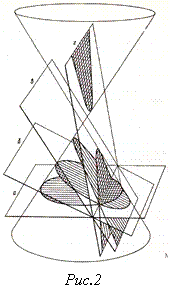
Аполлоній розглядає загальний випадок утворення конічних перерізів при перетині довільного кругового двопорожнинного конуса площиною під будь-яким кутом (рис.2). Вчений дістає еліпс, параболу або гіперболу залежно від того, перетинає площина всі твірні тільки однієї порожнини конуса, паралельна вона одній твірній чи перетинає обидві порожнини. Аполлоній ввів назви параболи, гіперболи й еліпса.

Для кожної з цих кривих Аполлоній відкриває і доводить основні її властивості. Зокрема, за основу класифікації кривих прийнято, по суті, властивості їх алгебраїчних рівнянь, які Аполлоній записував в словесно-геометричній формі і називав симптотами кривої. З сучасного погляду можна сказати, що Аполлоній досліджував властивості конічних перерізів відносно прямокутної системи координат, у якій одна вісь збігалася з головним діаметром кривої (в еліпса – це була велика вісь), а друга – проходила через вершину кривої.

2. Зародження аналітичної геометрії як розділу математики. В математичному природознавстві конічні перерізи тривалий час не знаходили застосування (хіба що крім параболічних дзеркал). Криві другого порядку привернули увагу вчених у XVI ст., коли невтомний шукач розгадок таємниць природи Й.Кеплер (1571–1630) поборов тисячолітню традицію і дійшов висновку, що планети обертаються навколо Сонця не по колах, як у це вірили всі від піфагорійців до Коперніка, а по еліпсах, в одному з фокусів яких знаходиться Сонце. Англійський математик і фізик Ісаак Ньютон (1643–1727) не лише теоретично обґрунтував закони руху планет, але і довів, що кожне тіло під дією тяжіння іншого тіла може рухатися лише або по еліпсу, або по параболі, або по гіперболі. Зокрема, по цими кривими відбувається рух всіх комет Сонячної системи.

Отже, ідея Аполлонія відродилася лише у XVII ст.

Над питаннями аналітичної геометрії плідно працював французький математик XVII ст. П’єр Ферма.

У творі «Введення у вивчення плоских і тілесних місць», надрукованому вже після смерті вченого його сином, з великою ясністю і вичерпною повнотою викладення ставиться питання про зображення рівнянь за допомогою геометрії. Ферма знаходить, що рівняння зручно представляти геометрично, провівши два відрізки прямих під певним, краще за все прямим, кутом один до одного, взявши їх перетин за початок відліку. Позначаючи початок координат літерою 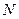, вісь абсцис літерою 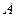, вісь ординат літерою , позначаючи також сталі величини літерами 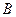, 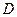і 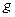, він отримав рівняння прямої, яка проходить через початок координат, параболи, круга в такому вигляд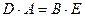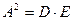і: , і .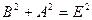

Слід відмітити, що записи Ферма для відповідних рівнянь ще в значній мірі відрізнялися від сучасних. Так вираз 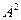записувався ним як 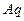, де 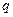– скорочення слова quadratum. Фактично рівняння прямої у Ферма записувалося наступним чином: « 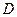на 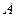дорівнює 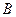на », а рівняння еліпса виражалося так: «Якщо 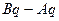має дане відношення до , то точка 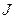знаходиться на еліпсі». Цей запис відповідає кресленню (рис.3).

Таким чином, у працях Ферма ми знаходимо вже всі необхідні дані для отримання алгебраїчних рівнянь, які виражають певні геометричні місця, тобто характерні риси аналітичної геометрії. Потрібно лише відмітити, що для своїх побудов Ферма обрав лише одну вісь (абсцис) і на ній відмічав вихідну точку (початок координат), від якої проводився відлік. Осі ординат як такої зовсім не було, а для кожної точки на площині Ферма, крім її абсциси враховував відстань від обраної вісі або за напрямом, перпендикулярним по відношенню до цієї вісі, або за похилою, тобто користувався прямокутними або косокутними координатами. Від’ємні відліки, тобто від’ємні абсциси або ординати, у працях Ферма зовсім були відсутні, але все ж таки він вільно виражав рівняння кола або еліпса, центр якого був розташований у початку координат, а більша вісь співпадала з віссю абсцис, хоча такі кола і еліпси мали точки з від’ємними абсцисами і ординатами.

Якщо два рівняння з двома невідомими відрізнялися лише сталими коефіцієнтами, то Ферма цілком справедливо вважав, що вони виражають криві одного і того ж характеру. Він встановив, що рівняння першого степеня представляють прямі, а рівняння другого степеня – конічні перерізи.

Праці Ферма у галузі аналітичної геометрії, можливо, мали б не менше значення для розвитку цієї науки, ніж роботи Декарта, який вважається її творцем, але більшість праць Ферма були приведені до порядку і опубліковані його сином вже після смерті їхнього автора, а тому праці Декарта і отримали пріоритет.

Завдяки своїй «Геометрії» Декарт набув слави основоположника аналітичної геометрії.

Головна ідея геометрії Декарта в тому, що геометричний об’єкт – крива лінія, подається рівнянням, яке пов’язує змінні величини. Досліджуючи властивості рівнянь, ми тим самим дістаємо інформацію і про властивості геометричних об’єктів. Це і дало підставу назвати потім геометрію Декарта аналітичною.

Декарт розглядав ще тільки одну пряму з фіксованою точкою відліку і вивчав властивості кривих ліній відносно цієї прямої. Однак це було вже велетенським кроком уперед. Метод координат не лише став однаковим способом символічного подання кривої у вигляді відповідного їй рівняння, він також давав необмежені можливості для введення в математику нових кривих, оскільки кожне довільно записане рівняння від двох змінних подавало якусь нову криву.

Декарт відійшов від давньої класифікації кривих на плоскі (прямі і кола), просторові (конічні перерізи) і лінійні (всі інші, такі, як спіраль) і ввів два нових класи: геометричні і механічні криві, тобто у сучасній термінології алгебраїчні і трансцендентні криві. Він вважав прийнятними лише перші і класифікував їх за степенем відповідного рівняння.

3. Подальший розвиток аналітичної геометрії. Дякуючи зручності методів і простоті алгоритмів аналітична геометрія одразу завоювала велику кількість прибічників і її первісні методи були розширені: Ф. ван Схоотен вивів у 1649 році формули заміни координат, Валліс (у 1655 році) розглянув від’ємні абсциси і ординати; Ньютон, а потім Яків Бернуллі винайшли полярні координати, в яких точки площини задавалися за допомогою фіксованої точки і променя, який з неї виходив (полярними координатами користувався ще Архімед у трактаті «Про спіралі»). Були досліджені нові криві: лемніската, логарифмічна спіраль, циклоїда та ін.

У XVIII ст. математики звернулися до фізики; це, як правило, потребувало доброго знання властивостей кривих і поверхонь: траекторії тіл, що рухаються представляють собою криві, тіла обмежені поверхнями.

Систематичне дослідження плоских алгебраїчних кривих вищих порядків привело до розширення відомих властивостей кривих. Наприклад, криві більше ніж другого порядку можуть мати особливості, які відсутні на кривих першого чи другого порядку: точки перегину, кратні точки, точки повернення (рис.4).

Були вивчені перетини кривих. К.Маклорен сформулював у своїй праці «Geometria organica»(1720 р.) таку властивість: «Дві плоскі алгебраїчні криві відповідно порядків і 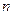мають взагалі спільних точок». Ейлер і Г.Крамер (1704–1752) без особливого успіху намагалися її довести, потім Е.Безу (1730–1783) дав більш повне доведення цієї властивості. Теорема отримала його ім’я.

Перший імпульс до вивчення поверхонь був даний спробами визначити форму Землі у відповідь на конкурс об’явлений Паризькою академією. Було розроблено представлення поверхні, зануреної у простір, рівнянням відносно трьох координат. Клеро ввів рівняння декількох поверхонь другого порядку (сфера, циліндр, параболоїд, двопорожнинний гіперболоїд, еліпсоїд), а Ейлер систематично вивчив загальне рівняння другого степеня від трьох змінних, яке представляє квадрики.

Клеро показав, що просторові криві можна описати як перетин двох поверхонь.

В наш час, коли навкруги Землі обертаються еліптичними орбітами тисячі штучних супутників, коли до Місяця, Венери, Марсу та інших планет Сонячної системи відправлені десятки космічних станцій, криві другого порядку використовуються ще інтенсивніше, ніж раніше.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Парабола	\|	Біографічна довідка

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.005 сек.