
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Предмет і задачі математичного програмування
деякі задачі управління і планування
Математичне програмування (МП) – це прикладна галузь математики, яка є теоретичною основою розв’язування задач оптимального планування.
Більшість планово-виробничих і економічних задач пов’язані з розподілом певних, як правило, обмежених ресурсів (сировини, робочої сили, різних видів палива і т.д.). Досить часто такий розподіл можна провести не єдиним чином. Наприклад, певну продукцію можна отримати різними способами, по-різному вибираючи технологію, сировину, обладнання. При цьому кожний спосіб розподілу ресурсів оцінюється з позицій деякого критерію (прибуток, об’єм випущеної продукції і т.д.) і характеризується певним значенням цього критерію. Очевидно, нашим завданням буде знаходження такого варіанту розподілу (програми, плану), який би гарантував найбільший економічний ефект.
Щоб використовувати методи МП для знаходження оптимального плану, економічну проблему треба записати за допомогою математичних виразів (рівнянь, нерівностей і т.д.), тобто скласти її математичну модель.
Математична модель – це система математичних виразів, яка описує характеристики об’єкта моделювання і взаємозв’язок між ними.Природно, що не завжди будь-яка математична модель адекватна модельованому об’єкту (процесу, явищу). Вона лише дає деяке наближене уявлення про нього. Для її побудови необхідно мати чітке розуміння мети функціонування досліджуваної системи.
Під метою будемо розуміти результат, який необхідно одержати шляхом вибору та реалізації певної програми дій (методів впливу) на досліджувану систему. В економічних задачах мета, як правило, полягає в тому, щоб максимізувати прибуток або мінімізувати витрати.
Коли мета визначена, виникає потреба у виборі способу дій, який би в найбільшій мірі сприяв її досягненню. Сам вибір способу дій визначається інформацією про обмеження, яким повинна задовольняти програма (план) дій.
Як мета, так і обмеження повинні бути представлені у вигляді функцій від змінних величин.
Реальні економічні процеси досить складні. При їх математичному описі потрібно враховувати множину різних факторів. Тому математична модель містить велику кількість умов з багатьма невідомими. Якщо невідомі входять в модель тільки в першому степені, то задача відноситься до розділу лінійного програмування, інакше – до нелінійного програмування. Оптимізаційні задачі, в яких потрібно враховувати послідовність дій або фактор часу, розглядаються в розділі динамічного програмування. Якщо в задачі параметри є випадковими величинами, то вона відноситься до задач стохастичної оптимізації.
До основних планово-виробничих і економічних задач відносяться:
· Задача про оптимальне використання ресурсів. Нехай для функціонування виробництва використовуються m різних видів сировини 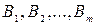 , обсяги яких відповідно становлять
, обсяги яких відповідно становлять 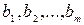 одиниць. Ці ресурси використовуються при виготовленні продукції виду
одиниць. Ці ресурси використовуються при виготовленні продукції виду  . Потреби ресурсу
. Потреби ресурсу  -го виду на виготовлення одиниці
-го виду на виготовлення одиниці  -го виробу позначимо через
-го виробу позначимо через 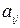 , а його ціну –
, а його ціну – 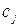 . Ефективність виробництва буде характеризуватися величиною отриманого прибутку від реалізованої продукції.
. Ефективність виробництва буде характеризуватися величиною отриманого прибутку від реалізованої продукції.
Потрібно визначити такий план випуску продукції, який максимізує прибуток підприємства при заданих ресурсах.
Запишемо дані у вигляді таблиці 1 і складемо математичну модель задачі.
Таблиця 1
| Види ресурсів | Види продукції | Запаси ресурсів | |||||
| А1 | А2 | … | Аj | … | An | ||
| В1 | а11 | а12 | … | а1j | … | а1n | b1 |
| В2 | a21 | a22 | … | a2j | … | a2n | b2 |
| … | … | … | … | … | … | … | … |
| Ві | ai1 | ai2 | … | aij | … | ain | bi |
| … | … | … | … | … | … | … | … |
| Вm | аm1 | am2 | … | amj | … | amn | bm |
| Прибуток | c1 | c2 | … | cj | … | cn |
Припустимо, що підприємство буде випускати х1 одиниць виробів виду А1, х2 – виду А2, …, хn – виду Аn. Очевидно, що повинні виконуватися обмеження:
 (1)
(1)
причому 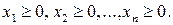
Потрібно скласти оптимальний план роботи підприємства, тобто знайти такі невід’ємні значення 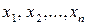 , які б задовольняли систему обмежень (1) і прибуток від реалізації продукції
, які б задовольняли систему обмежень (1) і прибуток від реалізації продукції 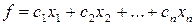 був би максимальним.
був би максимальним.
· Задача на складання дієти. Нехай маємо  продуктів харчування (м’ясні вироби, овочі, фрукти і т.д.), в кожному з яких міститься
продуктів харчування (м’ясні вироби, овочі, фрукти і т.д.), в кожному з яких міститься  видів поживних речовин (білки, жири, вуглеводи і т.д.). Відомо, що в одиниці
видів поживних речовин (білки, жири, вуглеводи і т.д.). Відомо, що в одиниці 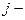 го продукту
го продукту  міститься
міститься 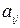 одиниць
одиниць  -ої поживної речовини
-ої поживної речовини 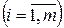 . Мінімальна добова потреба організму в
. Мінімальна добова потреба організму в  -ій поживній речовині становить
-ій поживній речовині становить  одиниць, а вартість одиниці продукту харчування
одиниць, а вартість одиниці продукту харчування  -го виду –
-го виду –  .
.
Потрібно скласти такий мінімальний за вартістю добовий раціон (набір і кількість продуктів харчування), щоб повністю задовольнити потреби організму в поживних речовинах.
Позначимо через 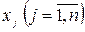 кількість одиниць продукту j-го виду, що використовується для добової потреби. Тоді загальна кількість i-ої поживної речовини, яка міститься в раціоні виразиться сумою
кількість одиниць продукту j-го виду, що використовується для добової потреби. Тоді загальна кількість i-ої поживної речовини, яка міститься в раціоні виразиться сумою
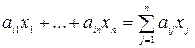 .
.
Ця сума має бути більша або рівна потрібного мінімуму  по всіх видах поживних речовин і математично виразиться формулою
по всіх видах поживних речовин і математично виразиться формулою
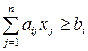 ,
, 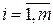 . (2)
. (2)
З іншого боку, добове споживання кожного виду продукту харчування обмежено наявними запасами  .
.
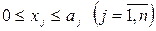 . (3)
. (3)
Сумарна вартість дієти
 . (4)
. (4)
Отже, оптимальною дієтою буде такий набір продуктів харчування, який перетворює в мінімум лінійну функцію (4) при умовах (2) і (3).
· Транспортна задача. В пунктах відправлення  знаходиться відповідно
знаходиться відповідно  одиниць однорідного вантажу, для постачання n споживачам
одиниць однорідного вантажу, для постачання n споживачам  в кількостях
в кількостях  одиниць кожному. Транспортні затрати на перевезення одиниці вантажу з і-го пункту відправлення в j-ий пункт споживання –
одиниць кожному. Транспортні затрати на перевезення одиниці вантажу з і-го пункту відправлення в j-ий пункт споживання –  .
.
Потрібно скласти такий план перевезень, тобто знайти, скільки одиниць вантажу потрібно відправити з і-го пункту відправлення в j-ий пункт споживання, щоб задовольнити потреби, а сумарні витрати на перевезення були б мінімальними.
Позначимо через 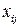 – кількість вантажу, який перевозиться з і-го пункту відправлення в j-ий пункт споживання. Тоді задача зводиться до визначення невідомих
– кількість вантажу, який перевозиться з і-го пункту відправлення в j-ий пункт споживання. Тоді задача зводиться до визначення невідомих 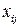 , які задовольняють умови:
, які задовольняють умови:
 (5)
(5)
Сформулюємо задачу МП в загальному вигляді: знайти значення n змінних 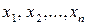 , які задовольняютьm рівнянням і нерівностям
, які задовольняютьm рівнянням і нерівностям
 (6)
(6)
і максимізують чи мінімізують функцію
 (7)
(7)
Умови (6) називаються обмеженнями, а (7) – цільовою функцією.
Зокрема, цільова функція в математичній формі виражає представлену мету з точки зору критерію оптимальності.
Керування економічним процесом полягає в тому, щоб вибрати такі значення змінних  , які б надавали функції ефективності (цільовій функції, функції мети) екстремального значення, тобто знайти
, які б надавали функції ефективності (цільовій функції, функції мети) екстремального значення, тобто знайти
F= 
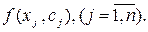
Набір керованих змінних 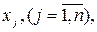 які задовольняють систему обмежень
які задовольняють систему обмежень  , називають допустимим розв’язком (планом), а набір керованих змінних
, називають допустимим розв’язком (планом), а набір керованих змінних 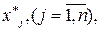 при яких цільова функція досягає екстремуму, – оптимальним.
при яких цільова функція досягає екстремуму, – оптимальним.
Читайте також:
- А є А, тобто усякий предмет є те, що він є.
- Абетково-предметний покажчик
- Алгебраїчне та інсерційне програмування
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі оптимізації в Excel
| <== попередня сторінка | | | наступна сторінка ==> |
| ТИПОВА ПРОГРАМА | | |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |