• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Матричні ігри. Розв’язування матричних ігор в чистих стратегіях

Нехай у кожного з двох гравців A і B скінченне число можливих дій – чистих стратегій: гравець A володіє m чистими стратегіями A₁, A₂, …, A_m, а гравець B – n чистими стратегіями B₁, B₂, …., B_n. Щоб гра була повністю визначена, необхідно вказати правило, яке кожній парі чистих стратегій (A_і;B_j )ставить у відповідність число a_ij – виграш гравця A за рахунок гравця B або програш гравця B. При a_ij<0 гравець A платить гравцю B суму . В грі, яка складається тільки з особистих ходів, вибір пари чистих стратегій (A_і;B_j) єдиним чином визначає її результат. Якщо ж в грі використовуються і випадкові ходи, то її результат обумовлюється середнім значенням виграшу (математичним сподіванням).

Якщо відомі значення a_ij виграшу для кожної пари (A_і; B_j)стратегій, то можна записати матрицю гри (платіжну матрицю)

Таблиця 3.1

Ai	Bj
B1	……….	Bn
A1		…….
…..	……	……..	……	…….
Am		……..
βj	β1	……..	βn

Платіжна матриця – це табличний запис функції виграшу. Описані ігри називають матричними. Окрема партія в такій грі реалізується наступним чином. Гравець A вибирає один із рядків платіжної матриці (одну з своїх чистих стратегій). Елемент матриці, який стоїть на перетині вибраного рядка і стовпця, визначає виграш гравця A (програш гравця B ).

Метою гравців є вибір найбільш вигідних стратегій, при яких гравець A вибирає максимальний виграш, а B – мінімальний програш. В теорії ігор виходять з припущення, що кожен гравець вважає свого супротивника розумним і намагається не дати йому досягти найкращого результату.

Визначення 3.1. Стратегія гравця A називається оптимальною, якщо при її застосуванні виграш гравця A не зменшиться, якими б стратегіями не користувався гравець B.

Визначення 3.2. Стратегія гравця B називається оптимальною, якщо при її застосуванні програш гравця B не збільшується, які б стратегії не застосовував гравець A.

Враховуючи наведені визначення, гравець A аналізує матрицю виграшів наступним чином: для кожної своєї чистої стратегії A_і він визначає мінімальне значення , виграшу в залежності від застосованих гравцем B чистих стратегій B_j. Потім серед усіх мінімальних виграшів він шукає таку чисту стратегію A_i⁰, при якій цей виграш буде максимальний, тобто знаходить

. (3.1)

Визначення 3.3. Число , яке визначається рівністю (3.1), називається нижньою чистою ціною гри (максиміном).

Воно показує, який мінімальний виграш може отримати гравець A, застосовуючи свої чисті стратегії при будь-яких діях гравця B. Відповідна стратегія A_i⁰ гравця A називається максимінною.

Аналогічно, гравець B намагається максимально зменшити свій програш. Тому він для кожної чистої стратегії B_j шукає , а потім серед B_j (див. таблиця 3.1) знаходить стратегію B_j⁰, при якій його програш буде мінімальним, тобто

. (3.2)

Визначення 3.4. Число , яке визначається за формулою (3.2), називається верхньою чистою ціною гри (мінімаксом).

Воно показує, який максимальний програш може бути в гравця B внаслідок використання чистих стратегій. Відповідна чиста стратегія B_j гравця B називається мінімаксною.

Таким чином, використовуючи чисті стратегії, гравець A забезпечує виграш не менше , а гравець В в результаті застосування своїх чистих стратегій може не дозволити гравцю A виграти більше, ніж .

Визначення 3.5. Принцип обережності, який диктує гравцям вибір максимінної і мінімаксної стратегій, називають принципом мінімакса.

Приклад 3.1. Знайти максимінну і мінімаксну стратегії в грі з матрицею

.

Розв’язок.Заповнимо для даної матриці таблицю 3.2

Таблиця 3.2

Ai	Bj
B1	B2	B3	B4
A1			-1		-1
A2
A3			-2	-1	-2
βj

, .

Отже, максимінною стратегією для гравця A є стратегія A₂, а мінімаксною стратегією гравця B – стратегія B₃.

Зв’язок між нижньою чистою ціною гри і верхньою чистою ціною гри встановлює наступна теорема, яку ми сформулюємо без доведення.

Теорема 3.1. В матричній грі її нижня чиста ціна гри не перевищує верхньої чистої ціни , тобто .

Якщо в матричній грі нижня і верхня чисті ціни співпадають, тобто , то кажуть, що ця гра має сідлову точку в чистих стратегіях і чисту ціну гри .

Визначення 3.6. Позначимо через i^* і j^* номери чистих стратегій, при яких має місце рівність . Пару чистих стратегій гравців A і B, при яких досягається ця рівність, називають сідловою точкою матричної гри, а елемент платіжної матриці, який стоїть на перетині i^*-го рядка, j^*- го стовпчика, – сідловим елементом.

Сідловий елемент є найменшим в i^*-му рядку і найбільшим в j^*-му стовпчику, тобто 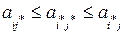. Тому, якщо гравець B відхилиться від своєї мінімаксної стратегії, його програш може збільшитися. Аналогічно відхилення гравця A від своєї максимінної стратегії веде до зменшення його виграшу. Таким чином, мінімаксні стратегії в грі з сідловою точкою мають властивість стійкості. Звідси випливає, що якщо в матриці гри існує сідловий елемент, то найкращими для гравців є їх мінімаксні стратегії.

Визначення 3.7. Чисті стратегії A_і* і B_j*, які утворюють сідлову точку і виділяють в матриці гри сідловий елемент, називаються оптимальними чистими стратегіями відповідно гравців A і B.

Визначення 3.8. Набір називається розв’язком гри.

Приклад 3.2. Знайти розв’язок гри, заданої матрицею

.

Розв’язок. Заповнимо для даної матриці таблицю 3.3.

Таблиця 3.3

	Ai	Bj
	B1	B2	B3	B4
A1
A2			-1	-3	-3
A3		-2	-5		-5
βj

, ,

. В даному випадку маємо дві сідлові точки (A₁, B₂) і(A₁, B₄). Отже, розв’язками гри будуть: {A₁; B₂; 2}і {A₁; B₄; 2}.

Читайте також:

1. Алгоритм розв’язування задачі
2. Алгоритм розв’язування задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі оптимізації в Excel
8. Аналіз перед розв’язуванням задачі
9. Аналіз перед розв’язуванням задачі
10. Вартість чистих активів і визначення фактичної доходності інвестиційного портфелю
11. Використання пакету Maple для розв’язування задач лінійного програмування
12. Геометрична інтерпретація ЗЛП. Графічний метод розв’язування

Переглядів: 5461