
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Геометрична інтерпретація ЗЛП. Графічний метод розв’язування
Для того, щоб краще зрозуміти суть розв’язування ЗЛП, яка записана в симетричній формі, з’ясуємо геометричний зміст системи лінійних нерівностей з двома невідомими.
Визначення 1.4. Множина  називається опуклою, якщо вона разом з точками
називається опуклою, якщо вона разом з точками  і
і  містить всі точки х відрізка
містить всі точки х відрізка  , тобто точки виду
, тобто точки виду 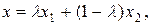
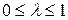 .
.
Розглянемо спочатку одну лінійну нерівність з двома невідомими 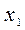 і
і 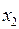 :
: 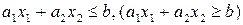 , яка визначає одну з півплощин, тобто справджується в точках однієї з півплощин, на які пряма
, яка визначає одну з півплощин, тобто справджується в точках однієї з півплощин, на які пряма  ділить координатну площину, і не справджується в точках іншої (пряма відноситься до кожної з півплощин). В цьому випадку кажуть, що дані нерівності визначають замкнену півплощину. В свою чергу, нерівності
ділить координатну площину, і не справджується в точках іншої (пряма відноситься до кожної з півплощин). В цьому випадку кажуть, що дані нерівності визначають замкнену півплощину. В свою чергу, нерівності 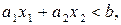 (
( 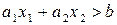 ) визначають відкриту півплощину.
) визначають відкриту півплощину.
Для визначення конкретної півплощини вибираємо довільну точку і перевіряємо чи правильна нерівність. Для зручності вибираємо  , якщо вона не належить граничній прямій. Якщо нерівність справджується, то розв’язком буде та півплощина, яка містить вибрану точку, в іншому випадку – яка його не містить.
, якщо вона не належить граничній прямій. Якщо нерівність справджується, то розв’язком буде та півплощина, яка містить вибрану точку, в іншому випадку – яка його не містить.
Наприклад, розв’язком нерівності 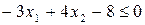 буде замкнена півплощина (рис.1.2), яка містить початок координат, а розв’язком нерівності
буде замкнена півплощина (рис.1.2), яка містить початок координат, а розв’язком нерівності 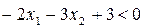 буде відкрита півплощина (рис.1.3), яка його не містить.
буде відкрита півплощина (рис.1.3), яка його не містить.
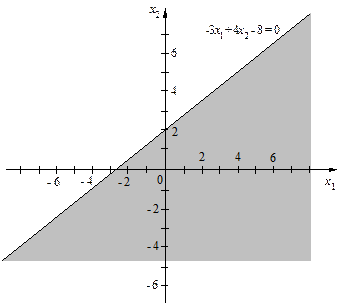
Рис.1.2


Рис.1.3
В першому випадку шукана півплощина лежить нижче прямої 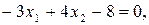 а в другому – вище прямої
а в другому – вище прямої 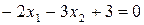 .
.
В найпростішому випадку система лінійних нерівностей з двома невідомими складається з двох нерівностей 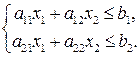
Ця система називається сумісною, якщо існують такі числові значення невідомих 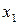 і
і  , які одночасно задовольняють обидві нерівності. Геометрично система сумісна, якщо в площині
, які одночасно задовольняють обидві нерівності. Геометрично система сумісна, якщо в площині 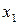 O
O  існують точки, координати яких задовольняють обидві нерівності. Якщо таких точок нема, то система нерівностей називається несумісною.
існують точки, координати яких задовольняють обидві нерівності. Якщо таких точок нема, то система нерівностей називається несумісною.
 На рисунку 1.4 показано внутрішню частину кута АВС, координати всіх точок якого є розв’язками системи нерівностей
На рисунку 1.4 показано внутрішню частину кута АВС, координати всіх точок якого є розв’язками системи нерівностей 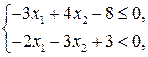 крім точок, що належать прямій ВС.
крім точок, що належать прямій ВС.


Рис.1.4
В свою чергу, розв’язком системи нерівностей  буде порожня множина. Дійсно, переписавши систему у вигляді
буде порожня множина. Дійсно, переписавши систему у вигляді 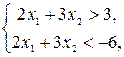 бачимо, що нерівності суперечливі між собою (рис.1.5).
бачимо, що нерівності суперечливі між собою (рис.1.5).



Рис. 1.5
Припустимо тепер, що задана деяка система лінійних нерівностей з невідомими 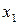 і
і  :
:
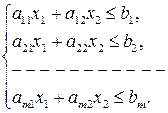 (1.2)
(1.2)
Сукупність розв’язків кожної з нерівностей цієї системи геометрично зображається множиною точок деякої півплощини, а сукупність всіх розв’язків системи (1.2) представляє собою деяку множину точок перетину (спільну частину) цих півплощин, границя якої складається з відрізків відповідних прямих.
Оскільки півплощина є опуклою множиною, то і множина розв’язків теж є опуклою. Назвемо її многокутною областю. Її також називають областю розв’язків системи нерівностей (1.2), або многокутником розв’язків. Зауважимо, що область розв’язків може бути многокутником, нескінченною множиною, смугою, що міститься між двома паралельними прямими, прямою, променем, відрізком, точкою, або порожньою множиною.
Приклад 1.2. Побудувати многокутник розв’язків системи нерівностей:
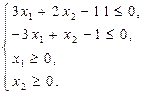
Розв’язок. Записуємо рівняння граничних прямих  ,
,  і будуємо їх на площині. Візьмемо
і будуємо їх на площині. Візьмемо  і визначаємо півплощини, які відповідають першим двом нерівностям системи. Взявши до уваги також нерівності
і визначаємо півплощини, які відповідають першим двом нерівностям системи. Взявши до уваги також нерівності 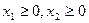 , дістанемо опуклий многокутник ОАВС, який є многокутником розв’язків заданої системи нерівностей (рис.1.6)
, дістанемо опуклий многокутник ОАВС, який є многокутником розв’язків заданої системи нерівностей (рис.1.6)


Рис.1.6
Враховуючи вищенаведені зауваження, переходимо до розв’язування прикладу 1.1.
Записуємо рівняння граничних прямих: 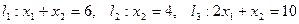 і будуємо їх на площинні.
і будуємо їх на площинні.
Підставляючи в кожну нерівність системи (1.1)  і
і 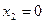 , визначаємо півплощини, які відповідають вихідним обмеженням-нерівностям.
, визначаємо півплощини, які відповідають вихідним обмеженням-нерівностям.
Враховуючи умови невід’ємності, отримаємо, що перетин (спільна частина) розглянутих півплощин представляє собою многокутник ОАВСD (рис.1.7)
 |
Рис.1.7
Будуємо вектор 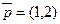 , координати якого рівні коефіцієнтам при
, координати якого рівні коефіцієнтам при 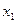 і
і 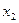 в цільовій функції, і перпендикулярно до нього пряму
в цільовій функції, і перпендикулярно до нього пряму 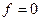 . Для визначення екстремальної точки переміщаємо пряму
. Для визначення екстремальної точки переміщаємо пряму 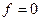 в напрямку вектора
в напрямку вектора 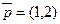 паралельно самій собі. Найбільш віддаленою точкою, в якій пряма
паралельно самій собі. Найбільш віддаленою точкою, в якій пряма 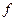 зустрінеться з областю допустимих розв’язків , буде точка В, яка є точкою перетину прямих
зустрінеться з областю допустимих розв’язків , буде точка В, яка є точкою перетину прямих  і
і  . Координати точки В є розв’язками наступної системи рівнянь
. Координати точки В є розв’язками наступної системи рівнянь 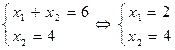 . Тоді
. Тоді  .
.
Отже, максимальна сума, отримана від реалізації прикрас, дорівнює 10 тис.грн. З них:  (тис.грн.) від реалізації прикрас виду
(тис.грн.) від реалізації прикрас виду  і
і  (тис.грн.) від реалізації прикрас виду
(тис.грн.) від реалізації прикрас виду  .
.
Цей метод розв’язування називається графічним і використовується для випадку, коли кількість невідомих  , або коли
, або коли  , де
, де 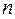 – число змінних задачі, а
– число змінних задачі, а 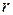 – ранг матриці системи обмежень. У випадку
– ранг матриці системи обмежень. У випадку  вже немає такої наглядної інтерпретації.
вже немає такої наглядної інтерпретації.
Сформулюємо тепер ЗЛП з двома змінними і вкажемо алгоритм її розв’язування.
Отже, ЗЛП в симетричній формі формулюється так: знайти найбільше значення функції
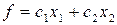 (1.3)
(1.3)
при обмеженнях
 (1.4)
(1.4)
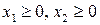 . (1.5)
. (1.5)
Як зазначалося вище, область розв’язків задачі (1.3) – (1.5) може бути многокутником, нескінченною областю, смугою, що міститься між двома паралельними прямими, точкою або порожньою множиною.
Функція (1.3) представляє собою на площинні 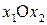 сім’ю паралельних прямих, кожній з яких відповідає певне значення
сім’ю паралельних прямих, кожній з яких відповідає певне значення 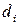 . Перпендикулярний до цих прямих вектор
. Перпендикулярний до цих прямих вектор 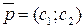 вказує напрямок найшвидшого зростання функції
вказує напрямок найшвидшого зростання функції  (рис.1.9) і ЗЛП (1.3) – (1.5) полягає в наступному: необхідно знайти точку допустимих значень, через яку проходить пряма сім’ї функцій
(рис.1.9) і ЗЛП (1.3) – (1.5) полягає в наступному: необхідно знайти точку допустимих значень, через яку проходить пряма сім’ї функцій  , і в якій функція
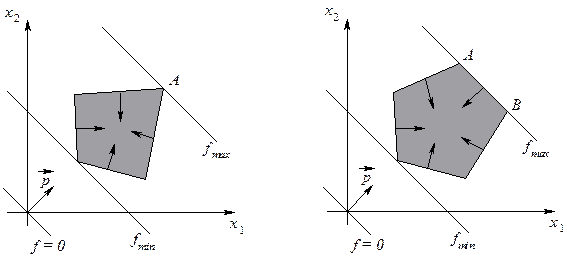
, і в якій функція  приймає найбільше значення (рис.1.9). При розв’язуванні ЗЛП графічним методом може трапитись, що задача (1.3) – (1.5) має:
приймає найбільше значення (рис.1.9). При розв’язуванні ЗЛП графічним методом може трапитись, що задача (1.3) – (1.5) має:
· єдиний розв’язок – координати точки А (рис.1.10.a);
· нескінченну множину розв’язків – координати будь-якої точки, що належить відрізку АВ (рис.1.10.б);
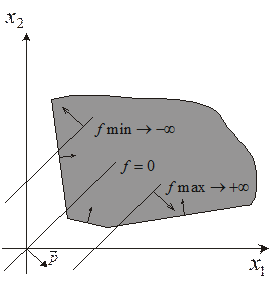
· функція  не досягає екстремального значення –
не досягає екстремального значення – 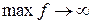 (рис.1.10.в).
(рис.1.10.в).

а) б)

в) г)
Рис. 1.8
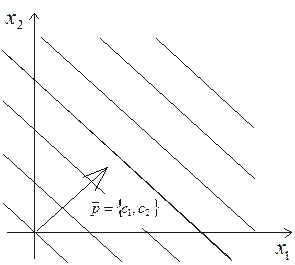
Рис.1.9
а) б)
в)
Рис.1.10
Розв’язування ЗЛП графічним методом проводиться в наступній послідовності:
1) записують рівняння граничних прямих  і будують їх на площинні
і будують їх на площинні 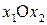 ;
;
2) визначають півплощину, яка відповідає вихідним обмеженням-нерівностям. Для цього беруть будь-яку точку і її координати підставляють в ліву частину обмеження-нерівності. Якщо вона при цьому перетворюється в правильну, то шуканою буде півплощина, яка містить цю точку, якщо ні, то шуканою буде півплощина, якій дана точка не належить;
3) виділяють область допустимих розв’язків задачі як спільну частину 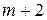 півплощин, де
півплощин, де 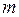 півплощин відповідають вихідним нерівностям (1.4), а дві півплощини – умові невід’ємності змінних
півплощин відповідають вихідним нерівностям (1.4), а дві півплощини – умові невід’ємності змінних 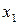 і
і  ;
;
4) будують вектор 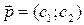 і перпендикулярно до нього одну із прямих сім’ї функцій
і перпендикулярно до нього одну із прямих сім’ї функцій  , наприклад,
, наприклад, 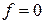 ;
;
5) визначаємо точку екстремуму на многокутнику розв’язків шляхом паралельного переміщення допоміжної прямої 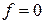 в напрямку вектора
в напрямку вектора  . Це буде найбільш віддалена крайня точка, в якій пряма
. Це буде найбільш віддалена крайня точка, в якій пряма  зустрінеться з областю допустимих розв’язків. Якщо необхідно знайти точку, якій відповідає мінімальне значення функції
зустрінеться з областю допустимих розв’язків. Якщо необхідно знайти точку, якій відповідає мінімальне значення функції  , то лінію рівня переміщаємо в напрямку вектора
, то лінію рівня переміщаємо в напрямку вектора  до перетину з першою точкою допустимої області (або пряму
до перетину з першою точкою допустимої області (або пряму 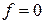 в напрямку вектора
в напрямку вектора 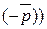 ;
;
6) знаходимо координати точки екстремуму і значення функції  в цій точці.
в цій точці.
Контрольні запитання та задачі
1. Назвіть основні типи планово-виробничих і економічних задач та дайте їх коротку характеристику.
2. Що називають математичною моделлю задачі?
3. Які змінні називають керованими?
4. Яка функція називається цільовою?
5. В чому суть керування економічним процесом (в термінах цільової функції)?
6. Як економічна задача зводиться до задачі на знаходження екстремального значення деякої функціональної залежності?
7. Дайте визначення допустимого та оптимального розв’язку?
8. Які задачі відносяться до ЗЛП?
9. Які ви знаєте форми запису ЗЛП? Дайте їх коротку характеристику.
10. Як відбувається перехід від однієї форми запису ЗЛП до іншої?
11. Чому для розв’язування ЗЛП не можна застосовувати методи диференціального числення?
12. Яка множина називається опуклою?
13. Який вигляд може мати область допустимих розв’язків ЗЛП з двома змінними?
14. Що представляє собою на площині 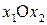 цільова функція і чим визначається напрям її найшвидшого зростання?
цільова функція і чим визначається напрям її найшвидшого зростання?
15. Що собою може представляти множина розв’язків ЗЛП?
16. Вкажіть основні етапи розв’язування ЗЛП графічним методом.
17. Їдальня реалізує три види власної продукції, використовуючи ресурси А1, А2, А3. Для виготовлення однієї партії виробів першого виду потрібно відповідно 3, 2, 4 одиниці ресурсів А1, А2, А3; для виготовлення однієї партії виробів другого виду – 2, 5, 3; третього виду — 6, 3, 5. Запаси ресурсів відповідно рівні: А1 – 76, А2 – 73, А3 – 83 одиниці. Прибуток від реалізації одиниці виробу першого, другого і третього видів становить 30, 40, 45 коп. Скласти математичну модель для визначення плану виробництва, що забезпечує максимальний прибуток, і записати задачу в канонічній формі.
18. Щоденно в місто привозять 20 т картоплі з трьох господарств: з першого – за ціною 650 грн., з другого – 660 грн., з третього – 610 грн. за тонну. Для своєчасного постачання картоплі необхідно затратити 9 год. 10 хв. на її навантаження. Відомо, що на навантаження 1 т картоплі в першому господарстві витрачається 20 хв., в другому – 30 хв., в третьому – 40 хв. Скласти математичну модель задачі мінімізації вартості завезеної картоплі, якщо з першого господарства можна завезти не більше 10 т, з другого – 6 т, з третього – 8 т, і записати задачу в канонічній формі.
19. Скласти математичну модель для визначення оптимального добового раціону відгодівлі свиней, якщо раціон однієї голови повинен містити 2,4 кг кормових одиниць, 360 г білка, 10 мг каротину. Раціон складається з трьох видів кормів: ячменю, бобів і трав’яної муки. В 1 кг ячменю міститься 0,8 кг кормових одиниць, 80 г білка, 2 мг каротину; в 1 кг бобів відповідно 0,9 кг, 180 г і 3 мг; в 1 кг муки – 0,6 кг, 100 г і 5 мг. Ціна 1 кг ячменю – 50 коп., бобів – 80 коп., муки – 65 коп. Критерій оптимальності – мінімум вартості раціону. Представити задачу в канонічній формі.
20. Для виготовлення виробів двох видів придбано 100 кг металу. На виготовлення виробу першого виду витрачається 2 кг металу; а другого –4 кг. Прибуток від реалізації виробу першого виду складає 3 грн., а другого – 2 грн., причому виробів першого виду потрібно виготовити не більше 40 штук, а другого – не більше 20 штук. Скласти математичну модель отримання максимального прибутку від реалізації виробів обох видів і представити задачу в канонічному вигляді.
21. Кондитерська фабрика для виготовлення трьох видів карамелі А, Б, В використовує три основні види сировини: цукор, патоку і фруктове пюре. Норми затрат цукру на виготовлення 1 т карамелі кожного виду відповідно рівні: 0,8; 0,5; 0,6 т; патоки – 0,4; 0,4; 0,3 т; фруктового пюре – 0; 0,1; 0,1 т. Запаси цукру – 80 т, патоки – 60 т, фруктового пюре – 12 т. Прибуток від реалізації карамелі виду А становить 1080 грн., виду Б – 1120 грн., виду В – 1260 грн. Скласти математичну модель для визначення плану виробництва, що забезпечує максимальний прибуток від діяльності фабрики, і записати задачу в симетричній формі.
22. Зобразити півплощини, які задаються нерівностями: а) 3х1–4х2+10  0; б) 3х1+х2
0; б) 3х1+х2 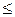 0; в) 2x1+3x2–12
0; в) 2x1+3x2–12 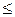 0; г) 2x1–3x2
0; г) 2x1–3x2  0.
0.
23. Знайти область розв’язків системи нерівностей:
а)

| б)

| в)

| г)

| ||||
д)

| е)
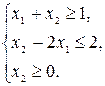
| є)

| |||||
24. Знайти найбільше та найменше значення функції f при умові, що змінні  невід’ємні.
невід’ємні.
а)
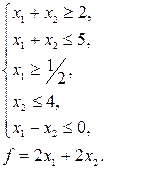
| б)

| в)

|
г)
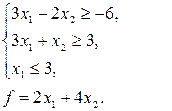
| д)
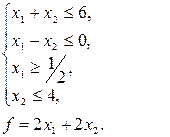
| е)
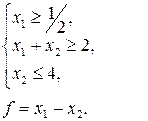
|
є)
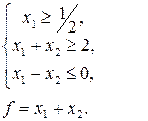
| ж)
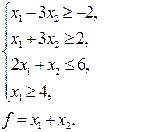
| з)

|
и)

| і)

| ї)

|
й)

| к)

| л)

|
1.3. Опорні плани ЗЛП
Розглянутий в 1.2 графічний метод застосовується до досить вузького класу ЗЛП. Універсальним методом розв’язування ЗЛП є симплексний метод. Перш ніж перейти до його розгляду, введемо нові поняття.
Визначення 1.5. Впорядкована система  чисел
чисел  називається
називається  -вимірним числовим вектором і позначається
-вимірним числовим вектором і позначається  а числа
а числа  називаються його координатами.
називаються його координатами.
Координати числового вектора можна розміщувати в рядок  і говорити про вектор-рядок, або в стовпчик
і говорити про вектор-рядок, або в стовпчик  і говорити про вектор-стовпчик.
і говорити про вектор-стовпчик.
Два числові вектори називаються рівними, якщо рівні їх відповідні координати. При додаванні двох числових векторів відповідні координати додаються, а при множенні числового вектора на число кожна координата множиться на це число.
Визначення 1.6. Система векторів  називається лінійно незалежною, якщо рівність
називається лінійно незалежною, якщо рівність 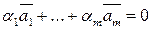 виконується тоді і тільки тоді, коли
виконується тоді і тільки тоді, коли 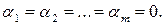
Визначення 1.7. Рангом 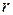 системи векторів називається найбільше число векторів, з яких можна утворити її лінійно незалежну підсистему.
системи векторів називається найбільше число векторів, з яких можна утворити її лінійно незалежну підсистему.
Визначення 1.8. Якщо ранг системи векторів 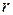 , то сукупність
, то сукупність 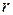 векторів цієї системи, які утворюють лінійно незалежну підсистему векторів, називається базисом цієї системи.
векторів цієї системи, які утворюють лінійно незалежну підсистему векторів, називається базисом цієї системи.
З n-вимірними числовими векторами ми зустрічатимемось при розв’язуванні лінійних рівнянь з n-невідомими, а також систем 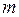 рівнянь з n невідомими.
рівнянь з n невідомими.
Справді, лінійне рівняння з  невідомими
невідомими  можна задати впорядкованою сукупністю
можна задати впорядкованою сукупністю  його коефіцієнтів, тобто
його коефіцієнтів, тобто  –вимірним вектором
–вимірним вектором  . Розв’язком буде вектор
. Розв’язком буде вектор 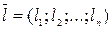 , який при підстановці в це рівняння перетворює його в тотожність.
, який при підстановці в це рівняння перетворює його в тотожність.
Визначення 1.9. Розв’язком системи 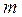 рівнянь з n невідомими
рівнянь з n невідомими 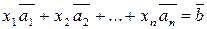 , де
, де 
називається кожний n-вимірний числовий вектор 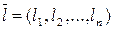 , який є розв’язком кожного з рівнянь системи.
, який є розв’язком кожного з рівнянь системи.
Систему рівнянь, яка має хоча б один розв’язок, називають сумісною, яка не має жодного розв’язку – несумісною. Сумісна система рівнянь, яка має один розв’язок, називається визначеною, а яка має безліч розв’язків – невизначеною.
Згідно з теоремою Кронекера-Капеллі сумісна система рівнянь є невизначеною, якщо ранг матриці системи менший від кількості невідомих.
Завдяки введеному поняттю n-вимірного числового вектора, ЗЛП записану в загальній, симетричній та канонічній формах, можна записувати в векторній формі. Зокрема, канонічна задача в векторній формі має вигляд: знайти найбільше значення функції 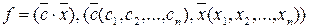 при обмеженнях
при обмеженнях
 , (1.6)
, (1.6)
де 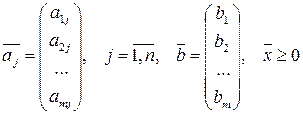 .
.
Зауваження 1.2. Для того, щоб можна було говорити про відшукання оптимального розв’язку вищенаведеної ЗЛП, треба, щоб система (1.6) була сумісною і мала безліч розв’язків. А це можливо в випадку, коли ранг 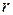 системи менший від числа невідомих
системи менший від числа невідомих 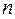 . Випадок
. Випадок 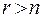 взагалі неможливий, а при
взагалі неможливий, а при  система має єдиний розв’язок і питання оптимального відпадає само по собі.
система має єдиний розв’язок і питання оптимального відпадає само по собі.
Нехай 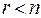 . В цьому випадку система
. В цьому випадку система  векторів
векторів  містить максимальну лінійно незалежну підсистему – базис, причому базисів може бути декілька, але не більше ніж
містить максимальну лінійно незалежну підсистему – базис, причому базисів може бути декілька, але не більше ніж  .
.
Визначення 1.10. Змінні, що відповідають 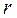 векторам базису, називають базисними, а решту
векторам базису, називають базисними, а решту 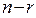 змінних – вільними.
змінних – вільними.
Припустимо, що один із базисів утворюють перші r векторів 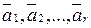 Йому відповідають базисні змінні
Йому відповідають базисні змінні 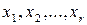 і вільні змінні
і вільні змінні 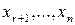 . При зроблених припущеннях систему (1.6) можна звести до вигляду:
. При зроблених припущеннях систему (1.6) можна звести до вигляду:
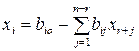
 (1.7)
(1.7)
в якому базисні змінні 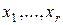 виражаються через вільні змінні
виражаються через вільні змінні 
Запис (1.7) задає загальний розв’язок системи (1.6).
Надаючи вільним змінним  в (1.7) певних числових значень, можна однозначно знайти відповідні значення базисних змінних, а, отже, і певний частинний розв’язок системи. Очевидно, що таких частинних розв’язків існує нескінченна множина.
в (1.7) певних числових значень, можна однозначно знайти відповідні значення базисних змінних, а, отже, і певний частинний розв’язок системи. Очевидно, що таких частинних розв’язків існує нескінченна множина.
Визначення 1.11. Частинний розв’язок, одержаний із загального при нульових значеннях вільних змінних, назвемо базисним розв’язком системи (1.6).
В цьому випадку з (1.7) знаходимо 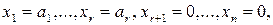 або
або  .
.
Оскільки кількість базисів не перевищує 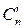 , а кожному базису відповідає свій базисний розв’язок, то і базисних розв’язків системи (1.6) буде не більше ніж
, а кожному базису відповідає свій базисний розв’язок, то і базисних розв’язків системи (1.6) буде не більше ніж 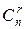 .
.
Визначення 1.12.Якщо в базисному розв’язку всі базисні змінні приймають невід’ємні значення, то його називають опорним розв’язком або опорним планом.
З даного визначення випливає, що опорний план не може містити більше ніж r додатних компонент.
Визначення 1.13. Опорний план, який містить рівно r відмінних від нуля компонент, називається невиродженим, якщо хоча б одна з базисних компонент дорівнює нулю, опорний план називається виродженим.
Сформулюємо ряд теорем, які обґрунтовують існування опорного плану для ЗЛП.
Теорема 1.1. Для існування хоча б одного опорного плану ЗЛП необхідно і досить, щоб ранг її сумісної системи обмежень, включаючи і обмеження змінних по знаку, дорівнював n.
Теорема 1.2. Якщо ЗЛП має розв’язок і серед планів цієї задачі є опорний, то хоча б один з них буде оптимальним.
Теорема 1.3. Якщо ЗЛП має хоча б один план і шуканий екстремум лінійної форми обмежений на множині планів, така ЗЛП має хоча б один оптимальний план.
Теорема 1.4. Якщо множина планів ЗЛП є непорожньою, то серед них є хоча б один опорний план, причому опорних планів може бути не більше, ніж 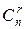 .
.
Для того, щоб дати геометричну інтерпретацію опорних планів, нам будуть потрібні деякі відомості з теорії систем лінійних нерівностей з 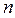 невідомими та теорії функцій багатьох змінних.
невідомими та теорії функцій багатьох змінних.
Сукупність  дійсних чисел
дійсних чисел  , записаних в певному порядку, називають точкою. Надалі точку
, записаних в певному порядку, називають точкою. Надалі точку  ототожнюватимемо з числовим вектором і позначатимемо
ототожнюватимемо з числовим вектором і позначатимемо 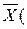
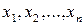
 . Числа
. Числа  називають координатами точки
називають координатами точки 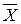 . На множині всіх таких точок введемо операції додавання і множення на дійсні числа за правилами
. На множині всіх таких точок введемо операції додавання і множення на дійсні числа за правилами 
 ,
, 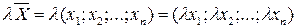 .
.
Множина всіх точок 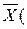
 із введеними вище операціями утворює n-вимірний лінійний точковий простір. Зокрема при
із введеними вище операціями утворює n-вимірний лінійний точковий простір. Зокрема при 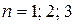 одержимо відповідно точки координатної прямої, координатної площини та координатного простору.
одержимо відповідно точки координатної прямої, координатної площини та координатного простору.
Відстань між двома точками  і
і 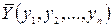 n-вимірного точкового простору визначатимемо за формулою
n-вимірного точкового простору визначатимемо за формулою
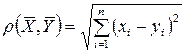 (1.8)
(1.8)
Точковий лінійний 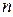 -вимірний простір, відстань між двома точками
-вимірний простір, відстань між двома точками 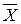 і
і  якого визначається за формулою (1.8), називають
якого визначається за формулою (1.8), називають  -вимірним евклідовим простором і позначають
-вимірним евклідовим простором і позначають  .
.
Нехай 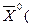
 та
та 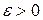 . Сукупність усіх точок
. Сукупність усіх точок 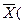
 простору
простору  таких, що
таких, що 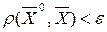 , називають
, називають  -вимірною кулею з центром у точці
-вимірною кулею з центром у точці  та радіусом
та радіусом  і позначають
і позначають  . Будь-яку кулю
. Будь-яку кулю  називатимемо сферичним
називатимемо сферичним  -околом точки
-околом точки  в просторі
в просторі  .
.
Нехай  – деяка множина точок
– деяка множина точок  -вимірного евклідового простору
-вимірного евклідового простору  . Точку
. Точку  називають внутрішньою точкою множини
називають внутрішньою точкою множини  , якщо існує окіл
, якщо існує окіл 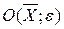 цієї точки, який міститься в множині
цієї точки, який міститься в множині  . Множину
. Множину  називають відкритою, якщо кожна її точка є внутрішньою. Точку
називають відкритою, якщо кожна її точка є внутрішньою. Точку 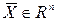 називають граничною точкою множини
називають граничною точкою множини  , якщо будь-який її окіл містить нескінченну кількість точок множини
, якщо будь-який її окіл містить нескінченну кількість точок множини  . Множину
. Множину  називають замкненою, якщо вона містить усі свої граничні точки.
називають замкненою, якщо вона містить усі свої граничні точки.
Геометричне місце точок 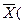
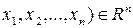 , координати яких є функції
, координати яких є функції 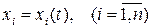 неперервні на відрізку
неперервні на відрізку  , називається неперервною кривою в просторі
, називається неперервною кривою в просторі 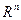 . Аргумент
. Аргумент 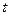 називається параметром кривої. Точка
називається параметром кривої. Точка  – початок кривої, а точка
– початок кривої, а точка  – її кінець.
– її кінець.
Множина  називається зв’язною, якщо будь-які дві її різні точки можна з’єднати неперервною кривою, яка повністю міститься в множині
називається зв’язною, якщо будь-які дві її різні точки можна з’єднати неперервною кривою, яка повністю міститься в множині  .
.
Зв’язна відкрита множина 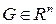 називається областю.
називається областю.
Точка 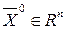 називається межовою точкою множини
називається межовою точкою множини  , якщо будь-який її окіл містить і точки множини
, якщо будь-який її окіл містить і точки множини  і точки, які їй не належать. Множина всіх межових точок множини
і точки, які їй не належать. Множина всіх межових точок множини  називається межею цієї множини. Область разом з її межею називається замкненою областю.
називається межею цієї множини. Область разом з її межею називається замкненою областю.
Нехай  – координати точки
– координати точки 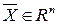 . Рівняння
. Рівняння  , не всі коефіцієнти якого нулі, визначає в просторі
, не всі коефіцієнти якого нулі, визначає в просторі  деяку гіперплощину. Крім точок, які належать даній гіперплощині, в
деяку гіперплощину. Крім точок, які належать даній гіперплощині, в  знайдуться точки для яких виконується
знайдуться точки для яких виконується  , і точки, в яких
, і точки, в яких 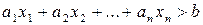 . Таким чином, в просторі
. Таким чином, в просторі 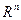 відносно деякої гіперплощини можна виділити дві частини (області), в точках яких виконуються вищенаведені нерівності. Ці області називаються відкритими півпросторами. Якщо до кожного з цих півпросторів приєднати гіперплощину, то отримаємо відповідні замкнуті півпростори.
відносно деякої гіперплощини можна виділити дві частини (області), в точках яких виконуються вищенаведені нерівності. Ці області називаються відкритими півпросторами. Якщо до кожного з цих півпросторів приєднати гіперплощину, то отримаємо відповідні замкнуті півпростори.
Визначення1.14. Якщо кожній точці 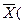
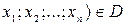 відповідає за певним законом одне і тільки одне дійсне число
відповідає за певним законом одне і тільки одне дійсне число  , то кажуть, що на множині
, то кажуть, що на множині  визначено функцію
визначено функцію 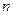 змінних
змінних  і записують
і записують 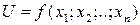 або
або  .
.
Розглянемо тепер нерівність  область розв’язків якої представляє собою один із півпросторів.
область розв’язків якої представляє собою один із півпросторів.
Тоді область розв’язків системи
 (1.9)
(1.9)
представляє деяку область  , що є перетином півпросторів, які визначаються її нерівностями.
, що є перетином півпросторів, які визначаються її нерівностями.
Область 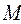 як перетин опуклих множин, є опуклою множиною, яку називають опуклою многогранною областю. Вона представляє собою область розв’язків системи нерівностей (1.9) – опуклий многогранник, який ще називають многогранником планів або многогранником допустимих розв’язків.
як перетин опуклих множин, є опуклою множиною, яку називають опуклою многогранною областю. Вона представляє собою область розв’язків системи нерівностей (1.9) – опуклий многогранник, який ще називають многогранником планів або многогранником допустимих розв’язків.
Таким чином, плани ЗЛП трактують як точки многогранника планів, а опорні плани є його вершинами. Має місце
Теорема1.5. Кожному опорному плану ЗЛП відповідає вершина многогранника планів, і, навпаки, кожній вершині многогранника планів відповідає опорний план ЗЛП.
Наведена теорема встановлює відповідність між опорними планами ЗЛП і вершинами многогранника планів. Зокрема, з неї випливає, що сукупність опорних планів співпадає з системою вершин многогранника планів. Оскільки опорних планів не більше ніж 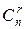 , то многогранник планів має скінченне число вершин.
, то многогранник планів має скінченне число вершин.
Визначення1.15. Точка 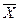 називається опуклою комбінацією точок
називається опуклою комбінацією точок  , якщо існують такі числа
, якщо існують такі числа  ,
, 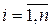 ,
,  , що
, що 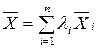 .
.
Вершиною (крайньою кутовою точкою) опуклої множини  називається точка цієї множини, яка не може бути представлена у вигляді опуклої лінійної комбінації з відмінними від нуля коефіцієнтами двох інших різних точок цієї множини.
називається точка цієї множини, яка не може бути представлена у вигляді опуклої лінійної комбінації з відмінними від нуля коефіцієнтами двох інших різних точок цієї множини.
Вершини опуклого многогранника мають властивість: будь-яку точку 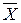 многогранника можна представити як опуклу лінійну комбінацію його вершин
многогранника можна представити як опуклу лінійну комбінацію його вершин 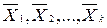 , тобто
, тобто 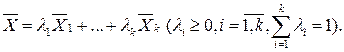
Розглянуту властивість вершин сформулюємо мовою планів: будь-який план ЗЛП можна представити як опуклу лінійну комбінацію її опорних планів. Із цього випливає, що для дослідження множини планів ЗЛП достатньо вивчати лише опорні плани.
Теорема1.6. Лінійна функція, визначена на опуклому n-вимірному многограннику, досягає найбільшого значення в вершині цього многогранника. Якщо лінійна функція досягає найбільшого значення більш ніж в одній вершині, то вона досягає такого ж значення в будь-якій точці, яка є опуклою лінійною комбінацією цих вершин.
Якщо функцію 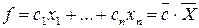 геометрично трактувати як сім’ю паралельних гіперплощин, кожній з яких відповідає певне значення
геометрично трактувати як сім’ю паралельних гіперплощин, кожній з яких відповідає певне значення 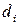 функції
функції  , то наведеній теоремі можна дати наступну геометричну інтерпретацію: гіперплощина ліній рівня лінійної функції
, то наведеній теоремі можна дати наступну геометричну інтерпретацію: гіперплощина ліній рівня лінійної функції  , яка відповідає її найбільшому значенню, проходить або через єдину вершину, або через ребро, або через грань многогранника планів, який визначається системою обмежень (1.6).
, яка відповідає її найбільшому значенню, проходить або через єдину вершину, або через ребро, або через грань многогранника планів, який визначається системою обмежень (1.6).
Оскільки кожній вершині многогранника відповідає опорний план, то можна сказати, що оптимальний план розв’язуваної ЗЛП співпадає принаймні з одним з її опорних планів.
Вектор 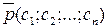 , перпендикулярний до гіперплощини, вказує напрям найшвидшого зростання функції f . Оскільки в будь-якій точці кожної гіперплощини функція f набуває сталого значення, то їх називають площинами рівня.
, перпендикулярний до гіперплощини, вказує напрям найшвидшого зростання функції f . Оскільки в будь-якій точці кожної гіперплощини функція f набуває сталого значення, то їх називають площинами рівня.
Враховуючи вищесказане, можна дати наступну геометричну інтерпретацію ЗЛП: знайти точку  многогранника планів, що визначається системою обмежень, через яку проходить гіперплощина сім’ї функції
многогранника планів, що визначається системою обмежень, через яку проходить гіперплощина сім’ї функції  і в якій функція
і в якій функція  приймає найбільше (найменше) значення.
приймає найбільше (найменше) значення.
Контрольні запитання та задачі
1. Дайте визначення n-вимірного числового вектора.
2. Яка система векторів 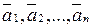 називається лінійно незалежною?
називається лінійно незалежною?
3. Що називається рангом системи векторів?
4. Що називається базисом системи векторів?
5. Що називають розв’язком лінійного рівняння з  невідомими?
невідомими?
6. Що називають розв’язком системи  рівнянь з
рівнянь з  невідомими?
невідомими?
7. Яку систему рівнянь називають сумісною (несумісною), визначеною (невизначеною)?
8. В якому випадку система рівнянь є невизначеною?
9. Як записується канонічна ЗЛП в векторній формі?
10. Які змінні називають базисними, а які – вільними?
11. Який розв’язок називають загальним, частинним, базисним і опорним?
12. Який опорний план називається невиродженим, а який виродженим?
13. Сформулюйте необхідну і достатню умову існування опорного плану.
14. Яке рівняння визначає гіперплощину в просторі  ?
?
15. Що собою представляє множина розв’язків системи  рівнянь з
рівнянь з  невідомими?
невідомими?
16. Дайте геометричну інтерпретацію плану і опорного плану ЗЛП
17. Дайте визначення опуклої комбінації точок  .
.
18. Дайте визначення вершини опуклої множини.
Читайте також:
- D) методу мозкового штурму.
- H) інноваційний менеджмент – це сукупність організаційно-економічних методів управління всіма стадіями інноваційного процесу.
- I Метод Шеннона-Фано
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- I. Метод рiвних вiдрiзкiв.
- VII. Нахождение общего решения методом характеристик
- А. науковий факт, b. гіпотеза, с. метод
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Агрегативна стійкість, коагуляція суспензій. Методи отримання.
- Агресивний тип дивідендної політики включає метод стабільного приросту дивідендів і метод постійного коефіцієнта виплат.
- АгротехнІЧНИЙ метод
- Адаптовані й специфічні методи дослідження у журналістикознавстві
| <== попередня сторінка | | | наступна сторінка ==> |
| Форми запису задач ЛП | | | Симплексний метод розв’язування ЗЛП (СМ) |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |