
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Форми запису задач ЛП
Розглянемо тепер конкретну задачу розподілу ресурсів.
Приклад 1.1.Ювелірна майстерня виготовляє прикраси двох видів  і
і  . Для цього використовуються дорогоцінні метали
. Для цього використовуються дорогоцінні метали 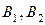 і
і  . Питомі витрати на одиницю виробу, запаси металів і вартості одиниці кожного виробу подані в таблиці 1.1:
. Питомі витрати на одиницю виробу, запаси металів і вартості одиниці кожного виробу подані в таблиці 1.1:
Таблиця 1.1
| Вид металу | Вироби | Запаси (гр) | |
| А1 | А2 | ||
| В1 | |||
| В2 | |||
| В3 | |||
| Вартість виробу (тис.грн.) |
Потрібно так організувати виробництво прикрас, щоб прибуток від їх реалізації був максимальним.
Розв’язок. Складемо математичну модель задачі. Припустимо, що для отримання найбільшого прибутку майстерня виготовить х1 виробів виду А1 і  виробів виду
виробів виду  . Кількість виробів невід’ємна:
. Кількість виробів невід’ємна: 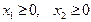 . Оскільки запаси кожного виду металів
. Оскільки запаси кожного виду металів 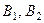 і
і  обмежені, то при відомих питомих витратах на одиницю виробу (див. таб. 1.1) змінні х1 і х2 повинні задовольняти наступним умовам:
обмежені, то при відомих питомих витратах на одиницю виробу (див. таб. 1.1) змінні х1 і х2 повинні задовольняти наступним умовам:
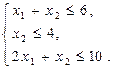 (1.1)
(1.1)
Вартість реалізованих виробів виразимо цільовою функцією  .
.
Таким чином, економічна задача в математичній формі формулюється так: знайти такі значення змінних  , які задовольняють умові
, які задовольняють умові  і при яких функція
і при яких функція  досягає найбільшого значення.
досягає найбільшого значення.
Розглядувана нами задача (приклад 1.1) є так званою задачею ЛП (ЗЛП). (До ЗЛП відносять такі, в яких всі функції  і
і  – лінійні відносно змінних. Якщо принаймні одна з функцій
– лінійні відносно змінних. Якщо принаймні одна з функцій  або
або  нелінійна, то відповідну задачу називають нелінійною).
нелінійна, то відповідну задачу називають нелінійною).
В ній, як зазначалося вище, потрібно відшукати значення змінних  (умови невід’ємності), які задовольняли б систему обмежень (1.1), і при яких цільова функція
(умови невід’ємності), які задовольняли б систему обмежень (1.1), і при яких цільова функція 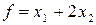 досягала б найбільшого значення.
досягала б найбільшого значення.
Проте в деяких задачах значення невідомих х1 і х2 повинні задовольняти лише деяку систему лінійних рівнянь, в інших – систему лінійних рівнянь і нерівностей, а також не обов’язково повинні бути невід’ємними. Поряд із задачами максимізації розглядають і задачі мінімізації.
В залежності від виду обмежень і критерію оптимальності розрізняють наступні форми запису ЗЛП:
a) загальна форма;
б) симетрична форма;
в) канонічна форма.
Визначення 1.1. Загальною ЗЛП називають задачу, в якій потрібно знайти найбільше (найменше) значення цільової функції

при обмеженнях
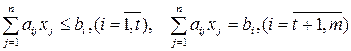 ,
, 
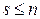 ,
,
де 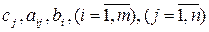 – задані дійсні числа.
– задані дійсні числа.
Визначення 1.2. ЗЛП в симетричній формі запису називають задачу, в якій потрібно знайти найбільше значення функції

при обмеженнях

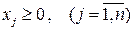 .
.
Визначення 1.3. ЗЛП в канонічній формі запису називають задачу, в якій потрібно знайти найбільше значення функції

при обмеженнях

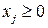 ,
, 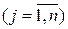 .
.
З’ясуємо тепер питання про взаємозв’язок між різними формами ЗЛП. Насамперед покажемо, що канонічну задачу можна перевести в симетричну і навпаки. Справді, рівняння 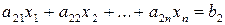 рівносильне системі нерівностей
рівносильне системі нерівностей

Тому, якщо кожне рівняння канонічної задачі замінити вище наведеною системою нерівностей, то отримуємо ЗЛП в симетричній формі.
З другого боку, нерівність  очевидно, рівносильна рівнянню
очевидно, рівносильна рівнянню  де
де 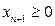 –додаткове невідоме. Рівносильність тут розуміється в тому сенсі, що кожному розв’язку нерівності
–додаткове невідоме. Рівносильність тут розуміється в тому сенсі, що кожному розв’язку нерівності  відповідає розв’язок рівняння
відповідає розв’язок рівняння 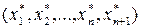 і навпаки.
і навпаки.
Отже, якщо кожну нерівність в системі обмежень симетричної задачі замінити рівносильним їй рівнянням, то симетрична задача набуде вигляду канонічної.
Симетрична і канонічна форми запису задачі є окремими випадками загальної задачі. Можна показати, що загальна задача може бути представлена у вигляді симетричної, а отже і канонічної форм.
При необхідності задачу максимізації можна замінити задачею мінімізації і навпаки.
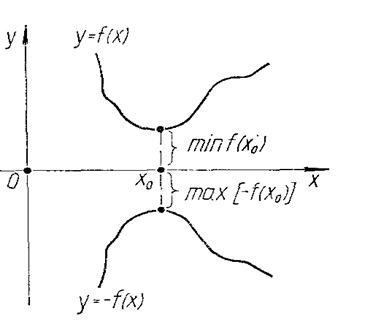
Рис. 1.1
Зауваження 1.1. Як відомо, задача знаходження екстремальних точок функції розв’язується методами диференціального числення, які дозволяють визначати тільки такі екстремальні точки, які знаходяться всередині розглядуваної області, а не на її границі. В ЗЛП оптимальні значення цільової функції досягаються завжди на границі многокутника розв’язків. Тому для дослідження таких задач потрібно використовувати спеціальні математичні методи.
Читайте також:
- А) Відносини власності і форми господарювання в сільському господарстві
- А) Заробітна плата її форми та системи.
- А) Заробітна плата, її форми та системи.
- А/. Форми здійснення народовладдя та види виборчих систем.
- Автоматизовані форми та системи обліку.
- Аграрні реформи та розвиток сільського госпо- дарства в 60-х роках XIX ст. — на початку XX ст.
- Акредитив та його форми
- Активні форми участі територіальної громади у вирішенні питань ММС
- Алгоритм розв’язання задачі
- Алгоритм розв’язання розподільної задачі
- Алгоритм розв’язування задачі
- Алгоритм розв’язування задачі
| <== попередня сторінка | | | наступна сторінка ==> |
| | | Геометрична інтерпретація ЗЛП. Графічний метод розв’язування |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |