• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Розв’язування матричних ігор в змішаних стратегіях

Нехай гра задана матрицею (табл. 3.4.)

Таблиця 3.4

	B1	B2	…	Bn	pi
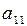
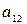
A1			…		р1
…	…	…	…	…	…
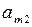
Am			…		pm
			…

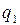
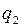
Через p₁, p₂, ..., p_m позначені ймовірності, з якими гравець A використовує чисті стратегії A₁, A₂, ..., A_m.; 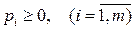, , а через 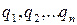ймовірності, з якими гравець 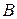використовує чисті стратегії ,

Визначення 3.9. Впорядкована множина P=(p₁; ...; p_m), елементи якої задовольняють умовам , і повністю визначають характер гри гравця A, називається його змішаною стратегією.

Таким чином, змішаною стратегією гравця A є повний набір ймовірностей застосування його чистих стратегій. Будь-яка його чиста стратегія A_і може розглядатися як частинний випадок змішаної стратегії, i-такомпонента якої дорівнює 1, а решта – 0, тобто

Визначення 3.10. Впорядкована множина Q=(q₁;...; q_n), елементи якої задовольняють співвідношенням і повністю визначають характер гри гравця В, називається його змішаною стратегією.

Нехай гравці A і B застосовують змішані стратегії P і Q. Це означає, що гравець A використовує стратегію A_і з ймовірністю р_і , а гравець B - стратегію B_j з ймовірністю q_j. Оскільки гравці вибирають свої чисті стратегії випадково і незалежно один від одного, то ймовірність вибору комбінацій стратегій (A 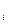,B_j) буде дорівнювати добутку ймовірностей p_iq_j. При використанні змішаних стратегій гра набуває випадкового характеру. Випадковою стає і величина виграшу гравця A (програшу гравця B). Тому тепер йдеться лише про середню величину виграшу (математичне сподівання). Ясно, що ця величина є функція від змішаних стратегій P і Q і визначається за формулою:

(3.3)

Визначення 3.11. Функція f(P,Q) називається платіжною функцією гри з матрицею (a_ij)_m´n.

Гравець A,змінюючи свої змішані стратегії P, намагається максимізувати середній виграш f(P,Q), а гравець B, змінюючи свої змішані стратегії Q –зробити цей виграш якомога меншим.

Для розв’язку гри з точки зору гравця A необхідно знайти такі змішані стратегії P і Q, при яких би забезпечувався середній виграш, що дорівнює

Визначення 3.12. Величина називається верхньою ціною гри, а величина – нижньою.

Визначення 3.13. Змішані стратегії P^* і Q^* гравців A і B, які задовольняють рівність

(3.4)

називаються оптимальними.

Визначення 3.14. Величина 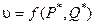, яка визначається формулою (3.4), називається ціною гри.

Дамо ще одне еквівалентне визначення оптимальних змішаних стратегій.

Визначення 3.15. Змішані стратегії P^* і Q^* гравців A і B відповідно називаються оптимальними змішаними стратегіями, якщо вони утворюють сідлову точку для платіжної функції f(P,Q), тобто задовольняють нерівності

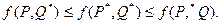(3.5)

З нерівностей (3.5) випливає, що в сідловій точці (P^*, Q^*) платіжна функція f(P,Q) досягає максимуму по змішаних стратегіях P гравця A і мінімуму по змішаних стратегіях Q гравця B.

Виявляється, що якщо використовувати змішані стратегії, то для будь-якої матричної гри можна знайти оптимальні стратегії і ціну гри. В цьому полягає зміст наступної теореми, яка в теорії ігор вважається основною і яку ми формулюємо без доведення.

Теорема 3.2. В змішаних стратегіях будь-яка скінченна матрична гра має сідлову точку.

Наступна теорема дає відповідь на питання: в якому випадку набір буде розв’язком гри.

Теорема 3.3. Для того, щоб змішані стратегії і були оптимальними для гравців A і B в грі з матрицею 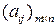і ціною гри , необхідно і достатньо виконання нерівностей

, (3.6)

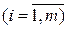. (3.7)

Дана теорема стверджує, що якщо гравець A застосує оптимальну змішану стратегію P^*, а гравець B – будь-яку чисту стратегію B_j, то виграш гравця A буде не меншим від ціни гри . Якщо гравець B використовує оптимальну змішану стратегію Q^*, а гравець A – будь-яку чисту стратегію A_і, то програшгравця B не перевищить ціну гри .

Розв’язок гри можна суттєво спростити, якщо своєчасно виявити в матриці гри домінування одних стратегій над іншими, оскільки це дозволяє скоротити розмірність матриці.

Зауваження 3.1. Якщо в матриці гри елементи k-го рядка не менші за відповідні елементи s- го рядка, тобто , то виграш гравця A при стратегії A_k буде більшим, ніж при стратегії 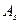, якою б стратегією не користувався гравець B. Тому для гравця A стратегія A_k буде вигіднішою, ніж стратегія 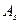. В зв’язку з цим кажуть, що стратегія A_k домінує над стратегією .

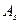Зауваження 3.2. Аналогічно, якщо елементи -го стовпчика не більші за відповідні елементи r-го стовпчика, тобто , то гравцю B при будь-яких умовах невигідно застосовувати стратегію B_r, оскільки в цьому випадку він буде програвати більше, ніж при використанні стратегії .

Приклад 3.3. Виконати всі можливі спрощення платіжної матриці

.

Розв’язок. Користуючись зауваженнями 3.1 і 3.2, отримаємо

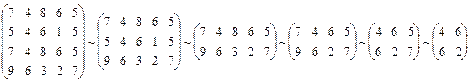
Наступна теорема широко використовується при спрощенні платіжних матриць.

Теорема 3.4. Нехай P^* і Q^*– оптимальні змішані стратегії гравців A і B в грі I з матрицею (a_ij)_{m´ n} і ціною . Тоді P^*і Q^* будуть оптимальними і в грі I^¢ з матрицею (ba_ij+c)_{m´ n} (b>0) і ціною

Приклад 3.4. Спростити платіжну матрицю

.

Розв’язок. Розділивши елементи матриці на 100 і додавши до одержаних значень 3, отримаємо .

Читайте також:

1. Алгоритм розв’язування задачі
2. Алгоритм розв’язування задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі оптимізації в Excel
8. Аналіз перед розв’язуванням задачі
9. Аналіз перед розв’язуванням задачі
10. Використання пакету Maple для розв’язування задач лінійного програмування
11. Геометрична інтерпретація ЗЛП. Графічний метод розв’язування
12. Графічний метод розв’язування задач лінійного програмування

Переглядів: 2458