• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Числові методи розв’язування матричних ігор

Розглянемо випадок, коли в матриці гри (a_ij)_m×nвсі a_ij>0. Ясно, що тоді і ціна гри . Знайдемо спочатку оптимальну змішану стратегію Q=(q₁;...;q_n) гравця B. Застосовуючи її, гравець B програє не більше від при будь-якій чистій стратегії A_i гравця A, тобто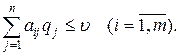

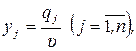Розділивши обидві частини останньої нерівності на , дістанемо , звідки, позначивши отримаємо

(3.8)

Крім того, 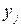задовольняє умові Гравець B намагатиметься зробити свій гарантований програш якомога меншим, а значить, якомога більшою величину

Таким чином, приходимо до наступної задачі: знайти найбільше значення функції

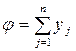(3.9)

при обмеженнях (3.8).

Це типова ЗЛП, записана в симетричній формі. Розв'язавши її, знайдемо оптимальний вектор і , а потім, використовуючи, що , , 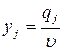визначимо ціну гри і компоненти оптимальної змішаної стратегії Q^*:

(3.10)

Міркуючи аналогічно, приходимо до задачі: знайти найменше значення функціїї

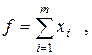(3.11)

при обмеженнях

(3.12)

розв'язуючи яку, знайдемо оптимальний вектор і .

Далі,

(3.13)

а оптимальна змішана стратегія гравця A буде

Задачі (3.8)–(3.9) і (3.11)–(3.12) утворюють пару двоїстих задач ЛП, а тому розв'язавши одну з них (наприклад, (3.8)–(3.9)), зразу можемо виписати розв'язки другої. Проілюструємо це на прикладі.

Приклад 3.4. Знайти розв'язок гри з матрицею

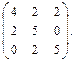
Розв'язок. Знайдемо спочатку оптимальну змішану стратегію гравця B. Для цього запишемо задачу (3.8)–(3.9): знайти найбільше значення функції при обмеженнях

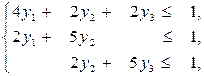
Ввівши змінні зведемо її до канонічної форми.

Розв’язуючи задачу СМ, приходимо до таблиці 3.5.

Таблиця 3. 5

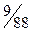
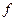
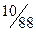
Оптимальний розв'язок За формулою (3.10) знаходимо ціну гри і Отже,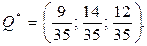

Задача для визначення компонент вектора , а отже, і компонент оптимальної змішаної стратегії P^* гравця A в канонічній формі має вигляд: мінімізувати функцію при обмеженнях

Тут базисними є змінні x₄, x₅, і x₆, а вільними – x₁, x₂, x₃. Враховуючи відповідності між змінними розглядуваної пари Д3, з таблиці 3.5 знайдемо За формулою (3.13) одержимо Таким чином, – оптимальна змішана стратегія гравця A.

При розв’язуванні матричних ігор розміром 2 ´ n і m ´ 2 доцільніше використовувати графічний метод і властивості оптимальних розв'язків пари ДЗ: якщо в оптимальному розв'язку задачі змінна додатна, то обмеження ДЗ, яке відповідає цій змінній, перетворюється в рівність. Якщо оптимальним розв'язком задачі обмеження перетворюється в строгу нерівність, то в оптимальному розв'язку ДЗ відповідна змінна рівна 0.

Приклад 3.5. Знайти розв'язок гри з матрицею

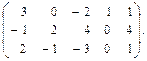
Розв'язок. Врахувавши відношення домінування рядків і стовпців і додавши до всіх елементів матриці число 5, отримаємо:

Для визначення оптимальних стратегій гравців складаємо пару ДЗ. Для гравця A знайти найменше значення при обмеженнях

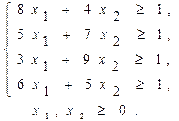(3.14)

для гравця B: знайти найбільше значення функції 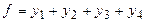при обмеженнях

(3.15)

Розв'язуючи задачу (3.14) графічним методом, знаходимо Оскільки то обидва обмеження в (3.15) її оптимальним розв'язком перетворюються в рівності. Крім того, при 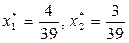перші два обмеження (3.14) перетворюються в строгі нерівності. Отже, відповідні змінні y₁ і y₂в оптимальному розв'язку (3.15) дорівнюють нулю (значить, . Для знаходження і залишається розв'язати систему рівнянь 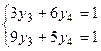. Звідки а отже , Крім того, 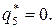Тоді, , а ціна гри

Читайте також:

1. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
2. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
3. Агрегативна стійкість, коагуляція суспензій. Методи отримання.
4. Адаптовані й специфічні методи дослідження у журналістикознавстві
5. Адміністративні (прямі) методи регулювання.
6. Адміністративні методи - це сукупність прийомів, впливів, заснованих на використанні об'єктивних організаційних відносин між людьми та загальноорганізаційних принципів управління.
7. Адміністративні методи управління
8. Адміністративні, економічні й інституційні методи.
9. Адміністративно-правові (організаційно-адміністративні) методи мотивації
10. Адміністративно-правові методи забезпечення економічного механізму управління охороною довкілля
11. Аерометоди
12. Активні групові методи

Переглядів: 555