• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Елементи теорії статистичних ігор

Ігри, в яких одним із учасників є людина (гравець ), а другим – природа (гравець П), називають статистичними. Під природою розуміють комплекс зовнішніх обставин, при яких доводиться приймати рішення, а гравця інколи називають статистиком.

Нехай статистик A використовує стратегії A₁…A_m, а природа П стратегії П₁;...;П_n. В своїх відносинах з природою статистик може користуватися як чистими стратегіями A_і, так і змішаними P=(р₁,...,р_m), р_i Якщо він має можливість оцінити наслідки застосування кожної своєї чистої стратегії A 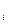в залежності від будь-якого стану П_j природи, тобто якщо йому відомий числовий результат a_ij для кожної допустимої комбінації (A_і, П_j), то статистичну гру можна задати платіжною матрицею (таблиця 3.6)

Таблиця 3. 6

Aі	Пj	Pі
П1	...	Пn
A1	a11	...	a1n	р1
...	...	...	...	...
Am		...		рm
		...

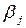
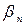
Приклад 3.6. На підприємстві використання сировини в залежності від її якості складає 10–12 одиниць. Якщо для випуску продукції сировини буде недостатньо, то запас її можна поповнити при затратах 5 одиниць на одиницю сировини, якщо ж запас сировини перевищує потреби, то затрати на зберігання залишків складають 2 одиниці на одиницю сировини. Скласти платіжну матрицю гри.

Розв’язок. Платіжна матриця гри задається таблицею 3.7

Таблиця 3.7

Ai	Пj
П1(10)	П2(11)	П3(12)
A1(10)		–5	–10	–10
A2(11)	–2		–5	–5
A3(12)	–4	–2		–4

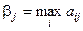
Розглянемо методи вибору оптимальної стратегії статистика.

Визначення 3.16. Ризиком 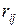статистика, коли він користується чистою стратегією A_i при стані П_j природи, називається різниця між максимальним виграшем 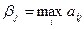, який він міг би дістати, достовірно знаючи, що природа реалізує стратегію П_{j ,} і тим виграшем a_ij, який він одержить, використовуючи стратегію А_i, не знаючи, який із станів П_j природа реалізує: .

Таблиця 3.8 представляє собою матрицю ризиків, а таблиця 3.9 матрицю ризиків для прикладу 3.6.

Таблиця 3.8 Таблиця 3.9

Ai

Пj

Ai

Пj

П1

...

A1

r11

...

r1n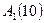

...

...

...

...

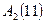
Am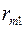

...

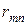
Розглянемо критерій вибору оптимальної стратегії статистика при невідомих ймовірностях станів природи.

Критерій Вальда – це максимінний критерій, і його можна сформулювати як для чистих, так і для змішаних стратегій. Він є критерієм крайнього песимізму, оскільки тут статистик виходить із припущення, що природа діє проти нього найгіршим чином, тобто реалізує такі свої стратегії П_j, при яких величина його виграшу приймає найменше значення – . Виходячи з того, статистик вибирає таку чисту стратегію A_i, при якій найменший виграш максимізується: .

Приклад 3.7. Користуючись критерієм Вальда, в умовах прикладу 3.6 знайти оптимальну стратегію.

Розв'язок. Виходячи з таблиці 3.7 прикладу 3.6, маємо 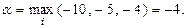Отже, оптимальною буде стратегія A₃.

Для змішаних стратегій критерій Вальда формулюється наступним чином: оптимальною змішаною стратегією статистика вважається та, при якій його мінімальний середній виграш буде максимальним, тобто змішана стратегія знаходиться з умови

Критерій Севіджа – це критерій мінімального ризику. Він мінімізує можливі втрати. Критерій Севіджа, як і критерій Вальда, є критерієм крайнього песимізму, оскільки тут статистик виходить з припущення, що природа діє проти нього найгіршим чином. Він рекомендує вибирати оптимальною ту чисту стратегію A_і, при якій мінімізується величина

Зауважимо, що з таблиці ризиків 3.9 випливає, що оптимальною за Севіджем буде чиста стратегія A₃, оскільки

При використанні критерію Севіджа в області змішаних стратегій розглядається середній ризик 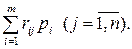Найнесприятливішим для статистика є такий стан П_j, при якому величина середнього ризику досягає найбільшого значення Критерій Севіджа рекомендує за оптимальну вибирати ту змішану стратегію P^*, при якій максимальне значення середнього ризику мінімізується:

Критерій Гурвіца – критерій песимізму-оптимізму, який рекомендує розраховувати на щось середнє. В області чистих стратегій оптимальною вважається стратегія, знайдена з умови

де 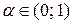і вибирається із суб'єктивних міркувань.

При 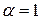критерій Гурвіца перетворюється в критерій Вальда, при 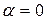– в критерій крайнього оптимізму: а при одержуємо дещо середнє.

Розглянемо тепер критерій вибору оптимальної стратегії статистика з використанням ймовірностей станів природи. В цьому випадку користуються як середнім значенням виграшу

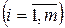, , (3.14)

так і середнім значенням ризику

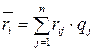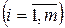, , (3.15)

які визначаються для кожної чистої стратегії статистика (таблиці 3.10 і 3.11, відповідно)

Таблиця 3.10 Таблиця 3.11

Ai	Пj		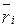	Ai	Пj
П1	...		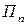	П1	...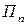
A1	r11	...	r1n			A1	a11	...	a1n
...	...	...	...	...		...	...	...	...	...
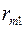
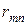
Am		...				Am		...
qj	q1	...	qn			qj	q1	...	qn

За оптимальну, згідно з критерієм Байєса, приймається чиста стратегія A_i, при якій максимізується середній виграш статистика, тобто

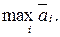
Аналогічно за оптимальну, відповідно до критерію Байєса, приймається чиста стратегія A_i, при якій мінімізується середній ризик.

Можна показати, що стратегія, яка максимізує середній виграш, співпадає з стратегією, яка мінімізує середній ризик.

Приклад 3.8. Припустимо, що в умовах прикладу 3.6 ймовірності q₁, q₂, q₃ споживання сировини в кількостях 10; 11 і 12 одиниць відповідно рівні 0,3; 0,1; 0,6. Знайти оптимальну стратегію, користуючись критерієм Байєса.

Розв’язок. Заповнимо таблиці 3.10 і 3.11.

Таблиця 3. 12 Таблиця 3.13

Ai	Пj			Ai	Пj
П1	П2	П3		П1	П2	П3
A1				6,5		A1		–5	–10	–6,5
A2				3,6			–2		–5	–3,6
A3				1,4		A3	–4	–2		–1,4
qj	0,3	0,1	0,6			qj	0,3	0,1	0,6

З таблиць видно, що стратегія A₃, яка максимізує середній виграш 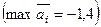, мінімізує середній ризик 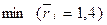. Отже, потрібно заготовити сировину в кількості 12 одиниць.

Зауваження 3.3. Якщо статистик не володіє об'єктивною інформацією про ймовірності q_j станів природи П_j і вважає в певній мірі правдоподібними всі стани, то їх ймовірності вибирають рівними

.

Згідно з критерієм Лапласа оптимальною вважається стратегія A_і, для якої .

Кожне управлінське рішення пов’язане з певним ризиком. Найбільш поширена точка зору, згідно з якою мірою ризику комерційного (фінансового) рішення або операції слід вважати середнє квадратичне відхилення значення показника ефективності цього рішення. Дійсно, чим менше розкидані результати рішення, тим менший ризик. Якщо ж варіація результатів дорівнює нулю, то ризик повністю відсутній.

З розглянутих вище прикладів випливає, що прийняте рішення (стратегія ) є однозначним. Проте це не завжди так, що проілюструємо на наступних прикладах.

Приклад 3.9. Розглядається два інвестиційних проекти. Перший з ймовірністю 0,6 забезпечує прибуток 15 млн.грн., а з ймовірністю 0,4 збиток в 5,5 млн.грн. Для другого проекту з ймовірністю 0,8 можна отримати прибуток в розмірі 10 млн.грн. і ймовірністю 0,2 збиток 6 млн.грн. Який проект вибрати?

Розв’язок. Обидва проекти мають однакову прибутковість, яка дорівнює 6,8 млн.грн. . Оскільки середнє квадратичне відхилення прибутку для першого проекту а для другого , тому вибираємо другий проект, оскільки .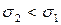

Приклад 3.10. Акціонерному товариству пропонуються два ризикових проекти:

№1:					;	№2:
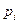
	0,2	0,6	0,2		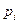0,4	0,2	0,4

Враховуючи, що акціонерне товариство має борг 80 млн.грн., вибрати вигідний проект (вигідну стратегію).

Розв’язок. Для оцінки ефективності розглядуваних інвестиційних проектів обчислимо 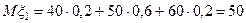(млн..грн.), (млн..грн.)

Оскільки середня прибутковість обох проектів однакова, шукаємо середньоквадратичні відхилення і :

,

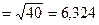. Таким чином, треба вибрати проект №1, тому, що при однаковій середній прибутковості ( =50 млн.грн.) ризик першого проекту набагато менший ніж ризик другого проекту . Проте для вибору проекту слід врахувати те, що акціонерне товариство має борг 80 млн.грн. Зокрема, якщо припустити, що дохідність проектів розподілена за нормальним законом, то згідно з правилом трьох сігм 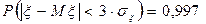, тобто з ймовірністю 0,997, її можливі значення будуть знаходитися в інтервалах:

Проект №1: .

Проект №2: .

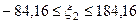Отже, при виборі менш ризикованого проекту №1 акціонерне товариство може суттєво зменшити свій борг, але від боргів воно повністю не звільниться.

Якщо ж буде вибраний більш ризикований проект №2, то акціонерне товариство може позбутися боргів, одержавши при цьому немалий прибуток. При невдачі його очікує банкрутство.

Контрольні запитання та задачі

Читайте також:

1. А .Маршалл - основоположник неокласичної теорії.
2. Адміністративне правопорушення як підстава юридичної відповідальності: ознаки і елементи.
3. Азот, фосфор, біогенні елементи та їх сполуки, органічні речовини
4. Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
5. Альтернативні теорії вартості
6. Альтернативні теорії вартості
7. Альтернативні теорії вартості
8. Альтернативні теорії капіталу
9. Альтернативні теорії макроекономічного регулювання
10. Альтернативні теорії максимізації
11. Альтернативні уявлення щодо макроекономічного регулювання: теорії раціональних сподівань та економіка пропозиції. Крива Лафера.
12. Аналіз статистичних даних про склад та плинність кадрів, які обіймали керівні

Переглядів: 947