• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Які ситуації називаються конфліктними?

2. Що вивчає теорія ігор?

3. Що таке гра, функція виграшу, стратегія, хід?

4. Які ігри називаються матричними?

5. Дайте визначення оптимальної стратегії гравця B.

6. Дайте визначення чистої нижньої ціни гри (максиміна) і верхньої чистої ціни гри (мінімакса).

7. Що показують нижня чиста ціна гри і верхня чиста ціна гри, і який між ними зв'язок ?

8. Що називається сідловою точкою, сідловим елементом матричної гри?

9. Які чисті стратегії гравців A і B називаються оптимальними чистими стратегіями?

10. Що називається розв'язком гри?

11. Що називають змішаними стратегіями гравців A і B?

12. Дайте визначення платіжної функції гри в змішаних стратегіях, нижньої і верхньої цін гри, оптимальних змішаних стратегій, ціни гри.

13. Сформулюйте необхідну і достатню умову того, щоб змішані стратегії P^* і Q­^* були оптимальними для гравців A і B.

14. Що називається ризиком статистика?

15. Сформулюйте критерії Байєса, Вальда, Севіджа, Гурвіца.

16. Знайти максимінну і мінімаксну стратегії в грі з матрицею:

а) 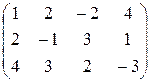;	б) ;	в) ;
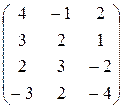г) ;	д) ;	е) .

17. Знайти сідлові елементи в грі з матрицею і записати розв’язок гри

а) 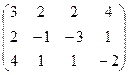;	б) 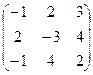;	в) ;
г) 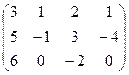;	д) .

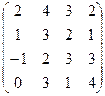18. Виконати всі можливі спрощення платіжної матриці:

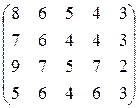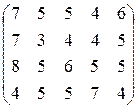а) ; б) ; в) ;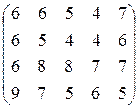

г) .

19. Знайти розв’язок гри з матрицею графічним методом:

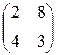а) ; б) ; в) ; г) .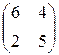

20. Знайти розв’язок гри з матрицею методом зведення до пари двоїстих ЗЛП

а) ; б) ; в) .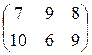

21. Статистична гра задана за допомогою матриці

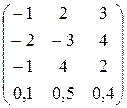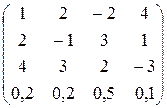а) ; б) ; в) .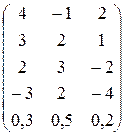

Користуючись критеріями Байєса, Вальда, Севіджа, Гурвіца при 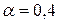знайти оптимальну стратегію статистика.

22. Акціонерному товариству пропонуються два проекти. Враховуючи, що акціонерне товариство має борг 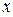, вибрати вигідний проект (вигідну стратегію):

а) б)

№1:		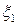				№1: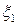
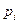
	0,3	0,4	0,3		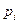0,2	0,3	0,5
№2:						№2:
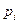
	0,4	0,2	0,4		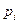0,1	0,2	0,7

х=30 х=50

23. Який з двох проектів менш ризикований, якщо перший з ймовірністю 0,7 забезпечує прибуток 18 млн.грн. і з ймовірністю 0,3 збиток в розмірі 6 млн.грн., а другий – з ймовірністю 0,6 прибуток в розмірі 20 млн.грн. і з ймовірністю 0,4 збиток в розмірі 3 млн.грн.

24. Який з двох проектів більш ризикований, якщо перший з ймовірністю 0,6 забезпечує прибуток 15 млн.грн. і з ймовірністю 0,4 збиток в розмірі 3 млн.грн., а другий – з ймовірністю 0,6 прибуток в розмірі 13 млн.грн. і з ймовірністю 0,4 збиток в розмірі 4,5 млн.грн.

Читайте також:

1. IV. Прийняття рішень у полі четвертої інформаційної ситуації
2. V. Прийняття рішень у полі п’ятої інформаційної ситуації
3. VI. Прийняття рішень у полі шостої інформаційної ситуації
4. Бюджетні установи отримують кошти на своє функціонування з бюджету виключно на основі фінансових документів, які називаються кошторисами.
5. В осередку надзвичайної ситуації
6. в осередку надзвичайної ситуації
7. Визначення ситуації
8. Визначення. Матриці, отримані в результаті елементарного перетворення, називаються еквівалентними.
9. Визначення. Точки максимуму й мінімуму функції називаються точками екстремуму.
10. Визначення. Числа й називаються комплексно спряженими.
11. Витрати одного блага, виражені в кількості іншого блага, яким довелося знехтувати (пожертвувати) називаються альтернативними витратами.
12. Геологічні ситуації.

Переглядів: 497