• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Детерміновані та стохастичні задачі ДП

Багатоетапні процеси, що розглядалися вище, характеризувалися тим, що результат будь-якого рішення однозначно визначався вибором розв’язку. Процеси такого типу називаються детермінованими. Для детермінованої моделі -етапного процесу стан системи (i=1,2,…, ) на кожному етапі задається вектором з однією або декількома компонентами. Перетворення вектора стану від етапу до етапу здійснюється внаслідок дії на нього вектором управління 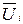, тобто 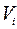( 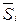; 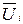) є функцією вектора стану і вектора управління на кожному етапі. Послідовність перетворень, починаючи з -го етапу і закінчуючи першим, можна записати так:

= ( ; ),

= ( ; ) (5.20)

………………………,

= ( ; ).

Якщо кожну попередню рівність (5.20) підставити в наступну, то одержимо кінцевий стан системи ,що виражається через початковий стан системи :

= ( (…( ( ; ))…))). (5.21)

Таким чином, існує послідовність векторів , , … , , що відповідає послідовності перетворень (5.20), яка називається поведінкою, або стратегією. Якщо перетворення вибрані в відповідності з певними критеріями, то множина оптимізуючих векторів управління називається оптимальною стратегією, або оптимальною поведінкою.

Тепер задачу максимізації повного доходу в -етапному процесі можна записати в наступному вигляді: знайти максимальне значення функції

W=

деg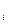 ( 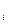; 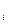) –дохід від i-го етапу, що є функцією вектора стану і вектора управління , W – загальний дохід.

Визначивши функцію 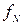( ) як максимальний дохід в -етапному процесі, починаючи з стану ( =1,2, … ) при використанні оптимальної стратегії отримуємо

( )=

Звідси, дотримуючись принципу оптимальності, приходимо до розглядуваних раніше функціональних рівнянь:

f ( )=

f ( )= (5.22)

f ( )= (5.23)

Необхідно відзначити, що в усіх розглянутих випадках загальний дохід має властивість адитивності, оскільки значення досягнуте за весь процес, ми отримували сумуванням його значень на певних етапах.

Нехай тепер на стан системи впливають випадкові фактори. В таких задачах управління процес не повністю визначається початковим станом системи і вибраним управлінням, а в деякий момент залежить від випадку. Такі задачі називаються стохастичними.

Стохастичні задачі мають місце тоді, коли: не можна точно визначити стан системи на кожному етапі; змінні, що характеризують стан системи, є випадковими величинами з відомою функцією розподілу; змінюється мета задачі; складається планування на тривалий період, оскільки в цьому випадку неможливо вказати значення всіх нормативів і коефіцієнтів, які змінюються під впливом непередбачуваних факторів, і т.д.

Для знаходження оптимального розв’язку багатоетапних екстремальних стохастичних задач з адитивними критеріями можна використати метод ДП. В стохастичній моделі перехід від -го етапу до ( )-го містить деяку невизначеність. В результаті перетворення 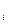( 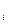; ) невідомий вектор стану S 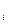переходить в випадковий вектор стану 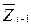з функцією розподілу G( 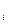; ; 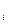), яка залежить від відомого стану 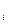, випадкового стану і управління . 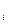Тому, перш ніж приймати рішення на ( )-му етапі, вважають, що дійсне значення вектора стану спостерігалось і є відомим.

Для стохастичного процесу, як і для детермінованого, можна схематично записати послідовність перетворень:

= ( ; ),

= ( ; ),

……………………,

= (; ),

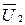але не можна за допомогою оберненої підстановки, як це було для детермінованих процесів, виразити кінцевий стан системи як функцію початкового. Це обумовлено тим, що результати перетворень відомі тільки після безпосереднього спостереження.

Величини 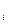є випадковими, тому їх використання дає невизначений результат для з’ясування величини критерію.

Функція

W= ,

як функція випадкових величин також є випадковою величиною, тому не може йтися про оптимальність. В зв’язку з цим за міру якості приймають деяку середню характеристику можливих результатів – математичне сподівання. Нехай

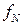( )= = , (5.24)

звідки для дискретного випадку маємо

f ( )= , (5.25)

де (j=1; 2; …; m) – ймовірності дискретних станів, які може приймати випадковий вектор , 0 ,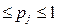

Більш детально стохастичні задачі розглянемо в наступному розділі.

Контрольні запитання та задачі

1. Сформулюйте задачу ДП.

2. В чому полягає суть принципу поетапної побудови оптимального управління ?

3. Сформулюйте задачу мінімізації витрат пального літака при набиранні висоти і швидкості.

4. В чому полягає суть методу функціональних рівнянь?

5. Складіть функціональне рівняння для багатоетапного процесу розподілу.

6. Запишіть функціональне рівняння загального виду для дискретного процесу і поясніть зміст величин, що входять в нього.

7. Сформулюйте задачу заміни обладнання і складіть функціональні рівняння, якщо вік обладнання відраховується в прямому, а етапи – в зворотному напрямках.

8. Складіть функціональні рівняння задачі заміни обладнання, якщо вік обладнання і етапи відраховуються в одному напрямку.

9. Які задачі називаються стохастичними?

10. В якому випадку мають місце стохастичні задачі?

11. Що приймають за міру якості поведінки системи при розв’язуванні стохастичних задач ДП?

12. Сформулюйте і виведіть функціональні рівняння задачі розподілу ресурсів в стохастичному варіанті.

13. На початок п’ятирічного періоду підприємству виділена сума 50000 грн. для придбання нового обладнання. Вартість одного комплекту обладнання – 5000 грн. Придбане обладнання відразу бере участь у виробничому процесі. Використання одного комплекту обладнання приносить підприємству за один рік прибуток в сумі 3000 грн. В кінці кожного року підприємство може виділити деяку долю a (0 £ a £ 1) прибутку на розширення виробничих потужностей. Потрібно так спланувати розширення виробництва, щоб прибуток за п’ятирічку був максимальним.

14. На початок п’ятирічного періоду підприємству виділена сума 30000 грн. для придбання нового обладнання. Вартість одного комплекту обладнання – 2500 грн. Придбане обладнання зразу бере участь у виробничому процесі. Використання одного комплекту обладнання приносить підприємству за один рік прибуток в сумі 1000 грн. В кінці кожного року підприємство може виділити деяку долю a (0 £ a £ 1) прибутку на розширення виробничих потужностей. Потрібно так спланувати розширення виробництва, щоб прибуток за п’ятирічку був максимальним.

15. Між двома галузями розподіляються 30000 грн. капітальних вкладень (КВ), причому у грн, вкладених в першу галузь, за рік приносить прибуток g(y)=0,7y. Залишок x – y вкладається в другу галузь і за рік приносить прибуток h(x-y)=0,6(x – y). На кінець року засоби, вкладені в першу галузь дорівнюють a(y)=0,4y, в другу – b(x–y)=0,7(x–y). По закінченні кожного року залишок КВ знову розподіляється між галузями. Потрібно так розподілити КВ між галузями, щоб сумарний прибуток за три роки був максимальним.

16. Між двома галузями розподіляються 20000 грн. КВ, причому у грн. вкладених в першу галузь, за рік приносить прибуток g(y)=0,8y. Залишок x–y вкладається в другу галузь і за рік приносить прибуток h(x–y)=0,5(x–y). На кінець року засоби, вкладені в першу галузь дорівнюють a(y)=0,3y, в другу – b(x–y)=0,6(x–y). По закінченні кожного року залишок КВ знову розподіляється між галузями. Потрібно так розподілити КВ між галузями, щоб сумарний прибуток за три роки був максимальним.

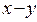17. Для розвитку двох галузей виробництва А та В на 3 роки виділено КВ. Кількість КВ , вкладених в галузь А, дозволяє отримати за один рік прибуток , і зменшується до величини . Кількість КВ , вкладених в другу галузь, дозволяє отримати за один рік прибуток , і КВ зменшується до величини . Необхідно розподілити виділені КВ за галузями виробництва і за роками планового періоду так, щоб повний дохід був максимальним.

18. Для розвитку двох галузей виробництва А та В на 3 роки виділено 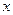КВ. Кількість КВ , вкладених в галузь А, дозволяє отримати за один рік прибуток , і зменшується до величини . Кількість КВ , вкладених в другу галузь, дозволяє отримати за один рік прибуток , і КВ зменшується до величини . Необхідно розподілити виділені КВ за галузями виробництва і за роками планового періоду так, щоб повний дохід був максимальним.

Читайте також:

1. Алгоритм розв’язання задачі
2. Алгоритм розв’язання розподільної задачі
3. Алгоритм розв’язування задачі
4. Алгоритм розв’язування задачі
5. Алгоритм розв’язування задачі
6. Алгоритм розв’язування задачі
7. Алгоритм розв’язування задачі
8. Алгоритм розв’язування задачі
9. Алгоритм розв’язування задачі оптимізації в Excel
10. Аналіз інформації та постановка задачі дослідження
11. Аналіз перед розв’язуванням задачі
12. Аналіз перед розв’язуванням задачі

Переглядів: 1066