Задача заміни обладнання

Прийняття рішення про заміну обладнання визначається такими чинниками, як продуктивність цього обладнання, експлуатаційні витрати, залишкова вартість обладнання, яка залежить від часу його експлуатації, і вартість нового обладнання.

Нехай r(t) – вартість продукції, що випускається за рік на одиниці обладнання, вік якого t років; l(t) – річні витрати на обслуговування цього обладнання; s(t) – залишкова вартість обладнання; p – вартість нового обладнання.

Потрібно визначити оптимальний цикл заміни обладнання на період часу тривалістю N років так, щоб за цей час дохід 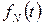від використання обладнання, вік якого t років, був максимальним.

В даній задачі вік обладнання будемо розглядати в прямому напрямку, а етапи, на які розбивається процес, – в зворотному. Таким чином, вік t=0 відповідає початку використання нового обладнання.

Складемо функціональне рівняння. Для цього знайдемо залежність між величинами, що входять в умову задачі на двох суміжних етапах. Якщо зберегти обладнання, вік якого t років, то дохід підприємства від його використання буде складатися з доходу на N-му етапі, рівного r(t)–l(t), і отриманого за N–1 етапів, при роботі на обладнанні, вік якого t+1 років, тобто

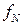(t)=r(t)–l(t)+ 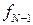(t+1). (5.12)

Якщо на -му етапі обладнання, вік якого t років, замінити новим, то дохід після такої заміни складається з доходу, отриманого як різниця сумарних вартостей s(t)+r(0) –p– l(0), де r(0) – вартість продукції, виготовленої на обладнанні, вік якого 0 років, а l(0) – експлуатаційні витрати, і доходу, отриманого за –1 етапів, що залишилися при роботі на обладнанні, вік якого 0+1 рік, тобто

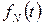=s(t) – p +r(0) – l(0) + 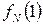(5.13)

Таким чином, якщо величина доходу (5.12) більша чи рівна величині доходу (5.13), то потрібно працювати на старому обладнанні, в іншому випадку обладнання необхідно замінити.

Об’єднавши (5.12) і (5.13), запишемо основне функціональне рівняння

f (t)= 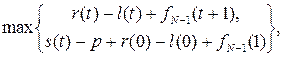(5.14)

де верхній рядок визначає дохід, який може бути отриманий при роботі на старому обладнанні, нижній – при його заміні. При цьому припускається, що перехід до роботи на новому обладнанні відбувається за один етап.

Поклавши в (5.14) =1, отримаємо функціональне рівняння одноетапного процесу, для якого доданки f i f не мають змісту, а тому із рівняння (5.14) виключаються:

(5.15)

Рівняння (5.14) і (5.15) дозволяють визначити величину в залежності від де при переході від одного етапу до другого вік обладнання збільшується від t до t+1, а число етапів, що залишилися, зменшується від до –1.

Зауваження 5.1. Якщо в задачі заміни обладнання вважати, що вік обладнання t і етапи відраховувати в прямому напрямку, то функціональне рівняння буде:

f (t)=max (5.16)

де верхній рядок визначає дохід при збереженні обладнання, нижній – при його заміні. Тут r (t) – вартість продукції, що виготовлена на -му етапі на одиниці обладнання, вік якого t років; l (t) – витрати на обслуговування одиниці обладнання, вік якого t років на N-му етапі; 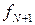(t+1) – дохід, отриманий на (N+1) -му етапі (рахуючи від кінця процесу), при роботі на обладнанні, вік якого (t+1) років; r (0) – вартість продукції, виготовленої на одиниці нового обладнання, вік якого – 0 років; u (t) =р - S (t) – витрати на заміну на -му етапі обладнання , вік якого - t років.

Зауваження 5.2. За допомогою функціональних рівнянь можна розв’язувати задачі заміни обладнання, які враховують різні фактори: вік обладнання, що закуповується, ремонт старого обладнання, обмеженість суми на придбання обладнання і т.д.

Нехай q (x; t) – ціна обладнання, (вік якого х років), що закуповується для заміни обладнання, вік якого - t років. В цьому випадку є три можливості: зберегти старе обладнання, купити нове, купити обладнання, вік якого х років. Розіб’ємо розглядуваний проміжок часу на N етапів. Тоді функціональне рівняння буде мати вигляд

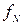(t)=max 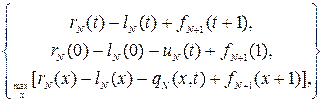(5.17)

де перший рядок визначає дохід при збереженні обладнання, другий – при заміні новим обладнанням, третій – при заміні обладнанням, вік якого – 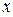років.

Нехай f (t ; t ) – величина доходу, яка може бути отримана при роботі на обладнанні, вік якого t років, останній ремонт якого проводився, коли його вік був t років. В цьому випадку можливі варіанти: зберегти, замінити і ремонтувати обладнання. Ці перспективи описуються за допомогою наступного функціонального рівняння:

f (t ;t )=max 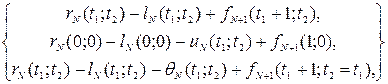(5.18)

де 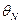(t ,t ) – вартість ремонту на -му етапі обладнання, вік якого t років, останній ремонт якого проводився в момент, коли воно прослужило t років. Інші позначення зберігають той самий зміст, що і раніше. В функціональному рівнянні (5.18) перший рядок визначає дохід при збереженні обладнання, другий – при заміні його новим обладнанням, третій – при ремонті.

Зауваження 5.3. Припустимо, що капітальні витрати на закупівлю обладнання обмежені деякою сумою М=С–С , де С – сума , що є на початку процесу; С - сума, витрачена на -му етапі. Тоді задача заміни обладнання описується функціональним рівнянням

f (t,C)=max (5.19)

в якому верхній рядок визначає величину доходу при збереженні, а нижній – при заміні обладнання.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Задача мінімізації витрат пального літаком при набиранні висоти і швидкості	\|	Детерміновані та стохастичні задачі ДП

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.