
МАРК РЕГНЕРУС ДОСЛІДЖЕННЯ: Наскільки відрізняються діти, які виросли в одностатевих союзах
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
Контакти
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Задача мінімізації витрат пального літаком при набиранні висоти і швидкості
Нехай літак, який знаходиться на висоті  і має початкову швидкість V0, повинен піднятися на висоту
і має початкову швидкість V0, повинен піднятися на висоту  і досягти швидкості
і досягти швидкості  . Відомі витрати пального на підняття літака з довільної висоти
. Відомі витрати пального на підняття літака з довільної висоти  на висоту
на висоту 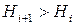 при сталій швидкості, а також витрати пального при збільшенні швидкості від довільного значення
при сталій швидкості, а також витрати пального при збільшенні швидкості від довільного значення  до значення
до значення  на заданій висоті. Потрібно знайти таке оптимальне управління набиранням висоти і швидкості, при якому загальні витрати пального були б мінімальними.
на заданій висоті. Потрібно знайти таке оптимальне управління набиранням висоти і швидкості, при якому загальні витрати пального були б мінімальними.
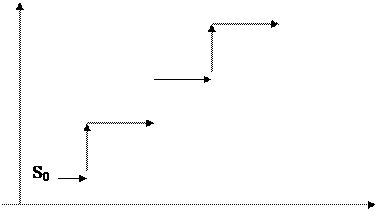
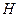
 S
S 

| ||||||

| ||||||

| ... |



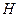 0
0



Рис.5.1.
Стан розглядуваної системи характеризується двома параметрами: швидкістю  і висотою
і висотою 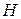 . Виходячи з цього, розв’язок будемо знаходити на координатній площині
. Виходячи з цього, розв’язок будемо знаходити на координатній площині 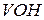 , в області D=
, в області D=  , яка представляє область допустимих розв’язків задачі (станів). Початковий стан S
, яка представляє область допустимих розв’язків задачі (станів). Початковий стан S  (
( 
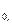
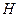
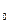 ) і кінцевий S
) і кінцевий S  (
( 
 ,
, 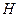
 ) на площині
) на площині  визначають конкретні дві точки S
визначають конкретні дві точки S 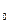 і S
і S  ( рис.5.1. ).
( рис.5.1. ).
Щоб віднайти розв’язок, розіб’ємо відрізки [ 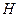

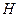
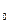 ] і [
] і [ 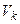

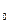 ] на n
] на n  і на n
і на n  рівних частин (етапів) і будемо вважати, що за один етап літак може збільшити висоту на величину
рівних частин (етапів) і будемо вважати, що за один етап літак може збільшити висоту на величину 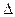
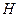 =(
=(  –
– 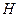
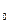 )/ n
)/ n  , або швидкість на величину
, або швидкість на величину
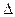
 =(
=( 
 –
– 
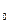 )/n
)/n  . Очевидно, що існує ціла множина траєкторій, які представляють собою сукупність ламаних ліній, по яких точка S може переміщатися з початкової точки S
. Очевидно, що існує ціла множина траєкторій, які представляють собою сукупність ламаних ліній, по яких точка S може переміщатися з початкової точки S 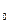 в кінцеву – S
в кінцеву – S  . Розв’язування задачі полягає в тому, що із множини управлінь потрібно вибрати таке, при якому загальні витрати пального W складаються з витрат пального на кожному етапі і будуть мінімальними. Можна простим перебиранням розглянути всі можливі траєкторії від S
. Розв’язування задачі полягає в тому, що із множини управлінь потрібно вибрати таке, при якому загальні витрати пального W складаються з витрат пального на кожному етапі і будуть мінімальними. Можна простим перебиранням розглянути всі можливі траєкторії від S 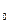 до S
до S  , визначивши при цьому витрати пального для кожної з них, і вибрати те управління, яке забезпечує найменші витрати.
, визначивши при цьому витрати пального для кожної з них, і вибрати те управління, яке забезпечує найменші витрати.
Такий підхід до знаходження розв’язку задачі є складним, оскільки при великих n  і n
і n  потребує значних часових затрат, навіть з використанням ПК. Набагато простіше розв’язок отримується методом ДП.
потребує значних часових затрат, навіть з використанням ПК. Набагато простіше розв’язок отримується методом ДП.
Читайте також:
- Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
- Автоматичне регулювання витрати помпових станцій
- Альтернативна вартість і незворотні витрати
- Аналіз витрат за центрами відповідальності.
- Аналіз витрат звичайної діяльності
- Аналіз витрат на 1 грн. вартості продукції
- Аналіз витрат на гривню товарної продукції
- Аналіз витрат на підприємстві за їх елементами та статтями калькуляції.
- Аналіз витрат.
- Аналіз динаміки і структури витрат підприємства
- Аналіз доходів і витрат підприємства
- Аналіз доходів та витрат від операцій з цінними паперами.
| <== попередня сторінка | | | наступна сторінка ==> |
| Задача про вибір найбільш економного маршруту постачання вантажу | | | Задача заміни обладнання |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |