
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
ЗАЛЕЖНІСТЬ ГУСТИНИ ПРЕСОВОК ВІД ТИСКУ ПРЕСУВАННЯ. ОСНОВНІ ТЕОРІЇ ПРЕСУВАННЯ
2.1. Основні визначення
При ущільненні порошкових матеріалів до значення густини, відповідній масі утруски, починається стадія ущільнення за рахунок пластичної деформації або крихкого руйнування частинок порошку. При цьому в точках контакту між частинками спочатку спостерігається пружна, а потім і пластична деформації, що призводить до збільшення площі опору між частинками і виникненню контактної поверхні.
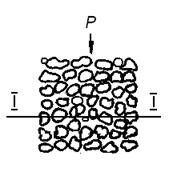
Рисунок 14 - Схема розташування одиночного шару в пресуванні
Для з'ясування терміну "контактна поверхня" розглянемо рисунок 14. Якщо провести площину I-I, перпендикулярну до напряму дії зусилля, то частинки, що потрапили в цей перетин, є "одиночним" шаром, який контактує з наступним шаром в окремих невеликих ділянках, розташованих під різними кутами по відношенню до площини перетину. Щоб знайти площу контактної поверхні, через яку зусилля від однієї частинки передається до іншої, необхідно площі всіх контактних ділянок "одиночного" шару спроектувати на площину I-I. Проекція контактної поверхні частинок одиночного шару на площину, перпендикулярну до напряму приложения тиску, називається контактним перетином SК.С..
Пластична деформація або крихке руйнування в контактному перетині починається тоді, коли напруга в цьому перетині стане більше критичного  .
.
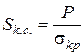 (17)
(17)
Якби матеріал в процесі деформації не зміцнювався, то площа контактного перетину змінювалася б прямо пропорційно зовнішньому тиску відповідно до приведеної залежності. У зв'язку з тим, що звичайно в процесі деформації матеріал зміцнюється, збільшується його твердість по Мейеру, а відповідно, і 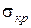 . Це призводить до того, що площа контактного перетину росте прямо пропорційно ступеню, відмінному від одиниці.
. Це призводить до того, що площа контактного перетину росте прямо пропорційно ступеню, відмінному від одиниці.
Встановлення залежності густини порошкового тіла, яке ущільнюється, від тиску пресування - основна задача як при розробці теорій пресування, так і при рішенні практичних задач. Знаючи ці залежності, легко розрахувати тиск, необхідний для отримання пресування заданої густини, а за оптимальним тиском можна розрахувати прес-форму для пресування конкретної деталі і вибрати відповідний прес.
В даний час розроблено декілька теорій пресування і запропоновано достатньо велику кількість рівнянь, що описують процес пресування тих або інших матеріалів. Більшість з них одержана емпіричним шляхом, тобто математичною обробкою експериментальних даних, тому вони з достатнім ступенем точності описують процес пресування лише тих порошків і за тих умов пресування, для яких вони були одержані.
Теоретичних рівнянь, виведених на основі яких-небудь фізичних явищ і передумов, значно менше. У зв'язку з тим, що фізичні явища, які впливають на процес пресування, складні і різноманітні, область застосування теоретично виведених рівнянь залежатиме від того, наскільки прийняті початкові передумови відображають фізику процесів пресування.
Однією з найбільш обгрунтованих теорій пресування, заснованої на дискретно-контактних уявленнях про формування порошків, є теорія Г.М.Ждановича, в якій він при виведенні рівнянь пропонує деформаційний механізм ущільнення порошкових тіл. Далі розглянемо характеристики цього механізму.
2.2. Деформаційний механізм ущільнення порошкових тіл
У основу своєї теорії Жданович поклав аналіз контактної взаємодії частинок порошкового тіла. При цьому частинка порошку розглядається як окреме тіло, що підпорядковується всім законам класичної механіки.
Для аналізу контакту між частинками розглядається модель, що складається з двох опуклих тіл, обмежених в околицях зони контакту деякими довільними криволінійними поверхнями (рис.15, 16). Первинна точка дотику тіл (частинок) приймається за початок координат. Осі X1 ,У1 і Х2, У2 розташовуються в загальній дотичній площині, а осі Z1 Z2 - по загальній нормалі.
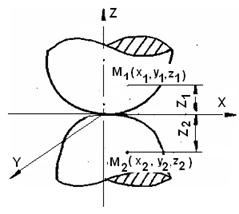
Рисунок 15 - Схема деформації частинок
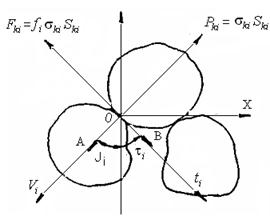
Рисунок 16 - Схема силової взаємодії частинок порошку при пресуванні
Передбачається, що в околиці зони контакту рівняння поверхонь дотичних частинок мають вигляд
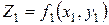 ;
; 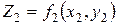 ; (18)
; (18)
При розкладанні цих функцій в ряди Маклорена одержимо:
 (19)
(19)
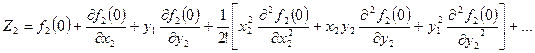 (20)
(20)
Індекс 0 у виразах (19) і (20) дає значення функцій Z1, і Z2, їх приватних похідних поблизу початку координат, тобто при 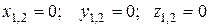 .
.
Оскільки Х0У - загальна дотична площина, то можна написати:
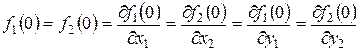 (21)
(21)
Тоді з урахуванням (21) рівняння (19) і (20) можна записати у вигляді:
 ; (22)
; (22)
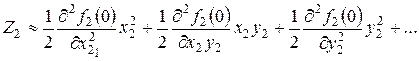 . (23)
. (23)
Якщо вісі, 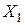 ,
, 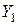 ,
,  , повернути так, щоб зникли члени ряду, що містять утворення
, повернути так, щоб зникли члени ряду, що містять утворення  і
і 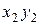 , і нехтувати членами порядку третьої і вищих ступенів, то рівняння (22) і (23) можна записати так:
, і нехтувати членами порядку третьої і вищих ступенів, то рівняння (22) і (23) можна записати так:
 (24)
(24)
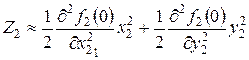 (25)
(25)
При деформації частинок (див. рис.15) крапки M1 і М2 можуть поєднатися і виявитися на контурі поверхні взаємного контакту частинок. Якщо ці зближення і поєднання відбуваються по осі Х, то в цьому випадку можна приблизно прийняти:
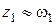 ;
;  ;
;  (26)
(26)
Де 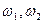 - нормальна контактна деформація частинок;
- нормальна контактна деформація частинок;  - зближення частинок.
- зближення частинок.
Підставляючи у вираз (26) значення  и
и 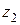 з рівнянь (22) і (23) одержуємо
з рівнянь (22) і (23) одержуємо
 (27)
(27)
Далі приймається, що квадрати координат прямо пропорційні розмірам площі контакту. Значення других похідних, які пов'язані з приведеною кривизною перетинів частинок, обернено пропорційні середньостатистичному розміру частинок aср. Тоді зближення частинок
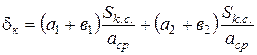 , (28)
, (28)
де
 ;
;
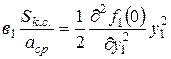 ;
;
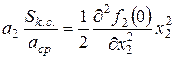 ;
;
 .
.
У остаточному вигляді вираз (28) записується так:
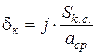 , , (30)
, , (30)
де
 , (31)
, (31)
або в диференціальній формі:
 . (32)
. (32)
Припускаючи, що деформація порошкового тіла відбувається в основному за рахунок нормальної деформації контактів частинок і їх відносного зрушення при збільшенні зусилля преса на  , можна розраховувати зміну висоти пресування:
, можна розраховувати зміну висоти пресування:
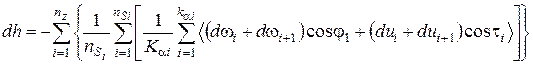 , (33)
, (33)
де  - висота пресовки в даний момент деформації;
- висота пресовки в даний момент деформації; 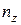 - приведене число шарів частинок по висоті пресовки;
- приведене число шарів частинок по висоті пресовки; 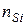 - число частинок в шарі пресовки, що розглядається;
- число частинок в шарі пресовки, що розглядається;  - число опорних контактів даної частинки;
- число опорних контактів даної частинки;  - елементарні, нормативні деформації контактів частинок, які взаємодіють;
- елементарні, нормативні деформації контактів частинок, які взаємодіють; 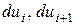 - елементарні зрушення, які є наслідком зміни контактів;
- елементарні зрушення, які є наслідком зміни контактів; 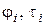 - кути відповідно нормальної і тангенціальної взаємодії контактів даних частинок (рис.16).
- кути відповідно нормальної і тангенціальної взаємодії контактів даних частинок (рис.16).
Переходячи до середньостатистичних величин і вважаючи, що

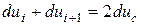
одержуємо
 (34)
(34)
або
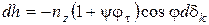 , (35)
, (35)
де
 ;
; 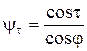 ; (36)
; (36)
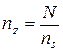 ; (37)
; (37)
N – загальне число частинок в пресовці; 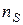 - середньостатистичне число частинок в даному шарі.
- середньостатистичне число частинок в даному шарі.
Визначивши загальне число частинок
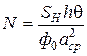 (38)
(38)
і середньостатистичне число частинок
 , (39)
, (39)
розрахуємо приведене число шарів частинок порошку по висоті пресування:
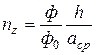 , (40)
, (40)
де 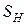 - номінальна площа перетинів пресування;
- номінальна площа перетинів пресування;  - коефіцієнт відповідно плоскої і об'ємної форми частинок.
- коефіцієнт відповідно плоскої і об'ємної форми частинок.
Підставляючи значення з виразу (40) в (35), знаходимо
 (41)
(41)
або щодо елементарного зближення частинок
. 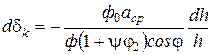 (42)
(42)
Середньостатистичне число контактів, що припадає на одну частинку з достатньою для практики точністю,
 , (43)
, (43)
де К - число контактів, що припадає на одну частинку при 100%-й густині порошкового тіла;  - відносна густина.
- відносна густина.
Проекція сумарної поверхні контактів в даний момент пресування
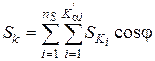 . (44)
. (44)
Виходячи з середньостатистичних величин вираз (44) може бути представлений так:
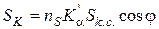 , (45)
, (45)
де 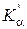 - середньостатистичне число опорних контактів частинки;
- середньостатистичне число опорних контактів частинки;  - середньостатистичний розмір майданчика контакту.
- середньостатистичний розмір майданчика контакту.
Число контактів мають частинки верхнього відкритого шару пресування, тому для його визначення використовується наступний вираз:
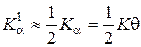 . (46)
. (46)
Розглядаючи спільно вирази (39) і (45), (46) визначаємо
 . (47)
. (47)
З (47) знаходимо
 (48)
(48)
де  - безрозмірна відносна величина проекції сумарної контактної поверхні пресування в даний момент пресування.
- безрозмірна відносна величина проекції сумарної контактної поверхні пресування в даний момент пресування.
Вважаючи постійним середній статистичний кут нормального контакту взаємодії частинок при пресуванні, можна знайти елементарний приріст середньостатистичної площі контакту 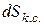 . При зміні зусилля преса на величину :
. При зміні зусилля преса на величину :
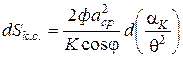 . (49)
. (49)
Надалі розглядаючи спільно вирази (32), (42) і (49) одержуємо:
 . (50)
. (50)
Даний вираз (50) є диференціальним рівнянням, що описує деформаційний механізм ущільнення порошкового тіла. Воно зв'язує приріст контактної поверхні пресування із зростанням її густини при збільшенні зусилля преса на 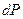 .
.
З (50) необхідно знайти величину, яку можна визначити при використанні принципу віртуальних переміщень, який для даного випадку формулюється так: "сума робіт всіх контактних, внутрішніх і інерційних сил на елементарних можливих переміщеннях дорівнює нулю". Ця умова записується так:
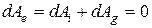 , (51)
, (51)
де 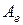 - елементарна робота зовнішніх сил,
- елементарна робота зовнішніх сил,
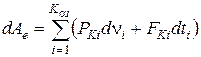 (52)
(52)
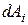 - елементарна робота внутрішніх сил,
- елементарна робота внутрішніх сил,
 , (53)
, (53)
 - елементарна робота інерційних сил,
- елементарна робота інерційних сил,
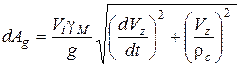 . (54)
. (54)
Робота вважається позитивною, якщо сила і переміщення направлені в одну сторону, і негативна, якщо в протилежні.
Для визначення елементарної роботи інерційних сил вважається, що робочий пуансон має постійну швидкість переміщення (  ).
).
Якщо розглядати частинку, що знаходиться в одиночному шарі порошкового тіла, яке ущільнюється, то зміну зусилля преса на величину  (рис.17) призведе до переміщення цієї частинки разом з шаром на величину
(рис.17) призведе до переміщення цієї частинки разом з шаром на величину 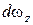 . Це переміщення - наслідок дії контактних сил. Елементарне переміщення шару частинок, що знаходиться на відстані від нижнього пуансона прес-форми, за умови відсутності сил зовнішнього тертя і постійності густини в об'ємі пресування, може бути визначено так:
. Це переміщення - наслідок дії контактних сил. Елементарне переміщення шару частинок, що знаходиться на відстані від нижнього пуансона прес-форми, за умови відсутності сил зовнішнього тертя і постійності густини в об'ємі пресування, може бути визначено так:
 . (55)
. (55)
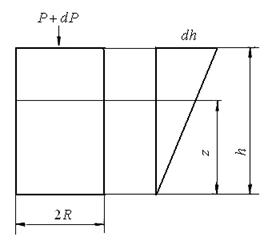
Рисунок 17 - Схема деформації пресування площею 
Тоді швидкість переміщення даного шару (частинки)
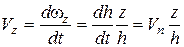 . (56)
. (56)
Відповідно прискорення
 . (57)
. (57)
Виходячи з прямолінійності руху частинки, радіус її траєкторії 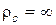 . Тоді при пресуванні з постійною швидкістю занурення елементарна робота інерційних сил може бути прийнята рівною нулю, тобто
. Тоді при пресуванні з постійною швидкістю занурення елементарна робота інерційних сил може бути прийнята рівною нулю, тобто
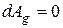 (58)
(58)
Елементарна робота зовнішніх сил
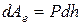 . (59)
. (59)
При цьому зусилля преса Р в даний момент пресування може бути визначене як сума проекцій всіх контактних сил частинок перетину пресування:
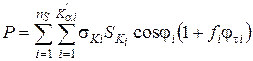 (60)
(60)
При переході до середньостатистичних величин вираз (60) можна записати так:
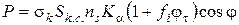 . (61)
. (61)
Тоді з урахуванням цієї залежності виразу (57) можна переписати
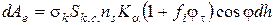 (62)
(62)
Елементарна робота внутрішніх сил, що витрачається на подолання сил відштовхування і зрушення частинок,
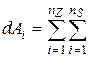 (63)
(63)
Цей вираз при переході до середньостатистичних величин можна переписати
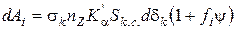 . (64)
. (64)
Підставляючи в умову (51) значення з (39), (40), (42), (58), (62) я (64), знаходимо:
 , (65)
, (65)
Розв`язуючи рівняння (65) щодо величини 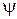 , одержуємо:
, одержуємо:
 . (66)
. (66)
Виходячи з припущення, що більшість частинок переміщається вертикально в напрямі, паралельному руху пуансона, для контактних зв'язків приймаємо умови:
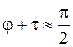 ;
; 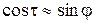 ;
;  . (67)
. (67)
Підставляючи ці значення у вираз (66), одержуємо:
 . (68)
. (68)
Диференціальне рівняння (50) можна записати так:
 , (69)
, (69)
де
 . (70)
. (70)
Інтеграція виразу (69) дає
 (71)
(71)
Постійна інтеграції С визначається з граничних умов при 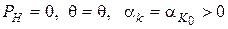 .
.
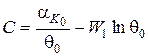 . (72)
. (72)
При,  звідки
звідки
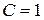 (73)
(73)
Розглядаючи обидва вирази (72) і (73) визначаємо
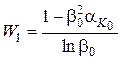 . (74)
. (74)
Підставляючи значення С з (72) і W1 з (74) в (71), одержуємо:
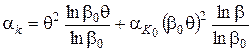 . (75)
. (75)
Оскільки відносний контактний перетин має дуже маленьку площу, для практичних розрахунків він може бути прийнятим рівним нулю, 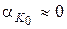 . Тоді вираз (75) можна записати:
. Тоді вираз (75) можна записати:
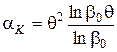 (76)
(76)
або, враховуючи, що,  ,
,
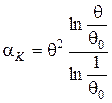 . (77)
. (77)
Вираз (77) є рівнянням, що описує деформаційний механізм ущільнення порошкового тіла при пресуванні.
Як відзначає Жданович, викладене дозволяє:
1. встановити залежність між середньостатистичними величинами зближення частинок при навантаженні порошкового шнура і площею проекції поверхні контакту на площину, перпендикулярну до лінії силової взаємодії (30), (32);
2. визначити взаємозв'язок між середньостатистичною величиною нормальної контактної деформації і густиною порошкового тіла (42);
3. встановити залежність між середньостатистичною величиною контактного майданчика і густиною порошкового тіла (48) і (49);
4. встановити взаємозв'язок між проекцією сумарної контактної поверхні пресування і її густиною (77). Як було відмічено раніше, дана закономірність визначає деформаційний механізм ущільнення порошкового тіла.
2.3. Рівняння пресування по Ждановичу
При виведенні своїх рівнянь Г.М.Жданович використовував два підходи. У одному випадку він виводить рівняння виходячи з рішення контактної задачі на підставі уявлень про деформаційний механізм ущільнення порошкового тіла.
Як було встановлено ним , зусилля пресування 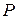 розглядається як сума проекцій опорних контактних сил всіх частинок перетину пресовки відповідно до рівняння (60):
розглядається як сума проекцій опорних контактних сил всіх частинок перетину пресовки відповідно до рівняння (60):

або при переході до середньостатистичних величин відповідно до рівняння (61):

Беручи до уваги, що середньостатистичне число частинок даного шару пресування 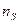 відповідно до (39)
відповідно до (39)
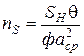 ,
,
а  і
і  відповідно до (46) і (47):
відповідно до (46) і (47):
 ;
;
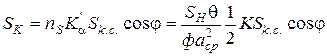 ,
,
визначаємо
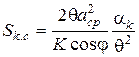 ,
,
де 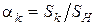 - безрозмірна відносна величина проекції сумарної контактної поверхні пресування в даний момент пресування.
- безрозмірна відносна величина проекції сумарної контактної поверхні пресування в даний момент пресування.
Підставивши значення (39), (46) і (48) в (61) і розділивши його на  , одержимо вираз для тиску пресування:
, одержимо вираз для тиску пресування:
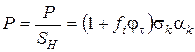 (78)
(78)
або з урахуванням того, що,  ,
,
 , (79)
, (79)
По Ждановичу контактне напруження для пластичних металів з урахуванням їх зміцнення при деформації в процесі ущільнення порошкового тіла пов'язано з відносною густиною пресування залежністю
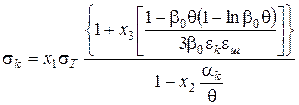 , (80)
, (80)
де  - постійні коефіцієнти, залежні від фізичних властивостей матеріалу частинок;
- постійні коефіцієнти, залежні від фізичних властивостей матеріалу частинок;
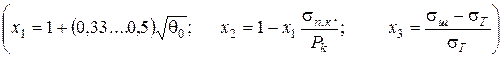 ;
;
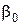 - відносний об'єм пресування в початковий момент пресування (відносний об'єм насипання);
- відносний об'єм пресування в початковий момент пресування (відносний об'єм насипання); 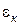 - приведена відносна деформація пресування при 100%-й густина пресування;
- приведена відносна деформація пресування при 100%-й густина пресування;  - відносна деформація, відповідна початку утворення шийки між частинками при їх деформації при ущільненні;
- відносна деформація, відповідна початку утворення шийки між частинками при їх деформації при ущільненні; 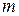 - показник зміцнення.
- показник зміцнення.
Для крихких матеріалів,  , а
, а 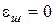 , тому
, тому
 (81)
(81)
і, отже, контактна напруга
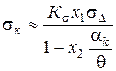 , (82)
, (82)
де 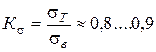 .
.
Підставляючи значення з (80) і (82) в (79), одержуємо рівняння для визначення тиску пресування порошків пластичних (83) і крихких (84) матеріалів:
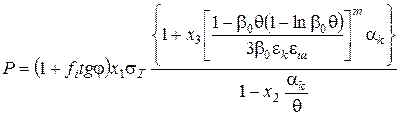 (83)
(83)
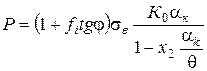 , (84)
, (84)
У ці рівняння входять змінні величини, 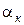 ,
, 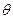 і
і  , що утрудняє їх практичне використання. У зв'язку з цим Жданович запропонував інтерполяційне рівняння:
, що утрудняє їх практичне використання. У зв'язку з цим Жданович запропонував інтерполяційне рівняння:
 , (85)
, (85)
де 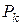 - тиск, необхідний для 100%-го ущільнення порошкового тіла;
- тиск, необхідний для 100%-го ущільнення порошкового тіла; 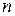 - показник ступеня, який необхідно визначити.
- показник ступеня, який необхідно визначити.
Для цього розглянемо спільно вирази (83), (84) і (85) і одержимо для випадку ущільнення порошків з пластичних матеріалів ( 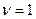 ):
):
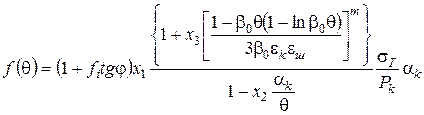 (86)
(86)
для крихких (  ):
):
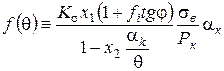 . (87)
. (87)
Інтерполяційна форма вибрана Ждановичем таким чином, що при певному значенні показника ступеня 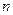 може бути досягнутий достатньо високий ступінь наближення. Видно, що початкова і критична краєві умови дотримуються при будь-яких кінцевих значеннях показника (
може бути досягнутий достатньо високий ступінь наближення. Видно, що початкова і критична краєві умови дотримуються при будь-яких кінцевих значеннях показника ( 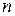 ),
),
якщо,  , то
, то  ,
,
а якщо  , то
, то  .
.
У зв'язку з цим показник ступеня доцільно визначати при деякому середньому значенні відносної густини пресування 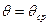 .
.
У якості такого середнього значення 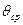 приймається як середня геометрична густина пресування
приймається як середня геометрична густина пресування  . При
. При 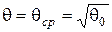 матимуть місце співвідношення:
матимуть місце співвідношення:
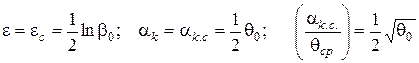 . (89)
. (89)
З урахуванням співвідношень (89) залежності (86) і (87) приймуть вигляд
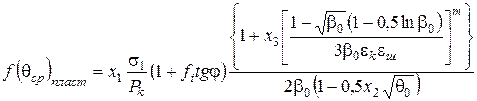 ; (90)
; (90)
 . (91)
. (91)
З інтерполяційної формули (85) виходить, що:
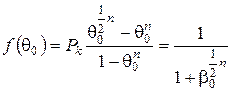 (92)
(92)
Вирішуючи цей вираз відносно  , одержуємо:
, одержуємо:
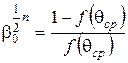 (93)
(93)
Далі вирішуючи вираз (93) відносно знаходимо:
 (94)
(94)
Таким чином, аналізуючи одержаний вираз (94), слід зазначити, що показник ступеня 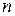 залежить від механічних властивостей порошку
залежить від механічних властивостей порошку 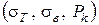 коефіцієнт контактного тертя
коефіцієнт контактного тертя  , відносної густини насипання .порошкового тіла (
, відносної густини насипання .порошкового тіла (  ), тобто практично від всіх чинників, що мають вплив на процес ущільнення порошкових матеріалів.
), тобто практично від всіх чинників, що мають вплив на процес ущільнення порошкових матеріалів.
Остаточне рівняння пресування, одержане Ждановичем має вигляд:
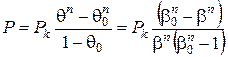 (95)
(95)
або відносно
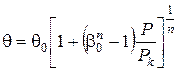 (96)
(96)
По Ждановичу можливий також інший підхід до рішення задачі про оптимальний тиск пресування. Оскільки пресування - складний процес пружно-пластичної деформації великого числа частинок, при якому і відносне розташування частинок, і картина їх взаємодії безперервно змінюються, висновок рівняння може бути обгрунтований виходячи не з деформації одиночного шару частинок, а з поведінки такої частини об'єму порошкового тіла, що складається з частинок з середнім розміром  , яка характеризує і зберігає всі фізичні властивості даного тіла, що знаходиться під тиском. Оскільки розмір пресованого виробу в більшості випадків більше 30
, яка характеризує і зберігає всі фізичні властивості даного тіла, що знаходиться під тиском. Оскільки розмір пресованого виробу в більшості випадків більше 30  , то можна застосувати гіпотезу суцільності.
, то можна застосувати гіпотезу суцільності.
У цьому випадку висновок рівняння пресування Жданович засновує на наступному:
1. Процес пресування порошкового тіла розглядається як процес пружно-пластичної деформації деякого умовного суцільного тіла, яке в процесі деформації зміцнюється і змінює свої розміри.
2. Частинка порошку, виділена з пресовки, що знаходиться під середнім тиском пресування ( 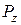 ) у даному перетині брикета, перебуває в рівновазі під дією системи сил, прикладених в місцях контакту -
) у даному перетині брикета, перебуває в рівновазі під дією системи сил, прикладених в місцях контакту - 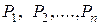 .
.
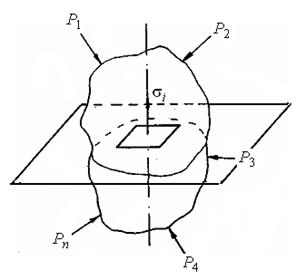
Рисунок 18 - Частина порошкового тіла, що знаходиться в рівновазі під дією зовнішніх сил
Під дією зовнішніх сил в тілі частинки виникають внутрішні сили. Нормальна складова напруг, створених внутрішніми силами в кожній точці частинки:
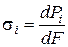 , (97)
, (97)
де 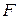 - площа поперечного перетину даної частинки в площині, перпендикулярній до напряму руху пуансона - осі
- площа поперечного перетину даної частинки в площині, перпендикулярній до напряму руху пуансона - осі  .
.
З урахуванням гіпотези суцільності передбачається, що фізичні всіх частинок однакові. Тоді напруги  , створені внутрішніми силами в даному перетині уздовж осі
, створені внутрішніми силами в даному перетині уздовж осі 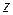 , будуть постійними, отже, виконуватиметься рівність
, будуть постійними, отже, виконуватиметься рівність
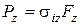 , (98)
, (98)
де 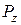 - зусилля преса;
- зусилля преса;  - площа "металевого" перетину пресування при зусиллі пресування
- площа "металевого" перетину пресування при зусиллі пресування 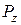 .
.
Щоб перейти до тиску пресування 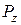 , обидві частини рівняння (98) необхідно розділити на площу перетину брикета
, обидві частини рівняння (98) необхідно розділити на площу перетину брикета 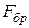 :
:
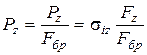 , (99)
, (99)
звідки
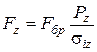 . (100)
. (100)
Оскільки із зростанням 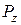 збільшуються
збільшуються  і
і  , то рівняння можна записати в диференціальній формі:
, то рівняння можна записати в диференціальній формі:
 , (101)
, (101)
тобто зміна площі металевого перетину прямо пропорційна зміні відношення  .
.
3. Відношення площі металевого перетину до номінальної площі
пресовки Жданович називає фактором суцільності 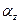 :
:
 , (102)
, (102)
де 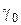 - початкова густина брикета;
- початкова густина брикета; 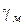 - густина компактного матеріалу;
- густина компактного матеріалу;  - початкова висота брикета;
- початкова висота брикета;  - поточна висота брикета.
- поточна висота брикета.
4. Процес деформації пористого брикета супроводжується зміцненням, яке пов'язане із збільшенням густини і зростанням контактної поверхні, наклепом частинок, і, отже, із збільшенням опірності деформації. Весь цей процес називається процесом сумарного приведеного, або ефективного зміцнення брикета.
Як критерій такого зміцнення може служити статечна функція від чинника сплошності:
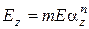 , (103)
, (103)
де 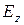 - модуль зміцнення пресування при тиску Р, кг/см2;
- модуль зміцнення пресування при тиску Р, кг/см2; 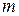 - коефіцієнт пропорційності, що враховує фізичні властивості матеріалу порошку, обумовлені способом його отримання;
- коефіцієнт пропорційності, що враховує фізичні властивості матеріалу порошку, обумовлені способом його отримання; 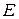 - модуль пружності матеріалу порошку;
- модуль пружності матеріалу порошку;  - чинник суцільності;
- чинник суцільності; 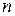 - показник зміцнення.
- показник зміцнення.
Підставивши у вираз (103) значення 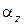 з (102), знаходимо:
з (102), знаходимо:
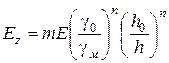 (104)
(104)
5. Внутрішні напруги в брикеті прямо пропорційні модулю зміцнення брикета і його відносної деформації:
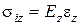 , (105)
, (105)
або
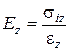 , (106)
, (106)
де
 ,
,
або в диференціальній формі
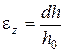 . (107)
. (107)
Знак "-" вказує на те, що приріст внутрішньої напруги пропорційний негативній зміні висоти брикета.
Тоді
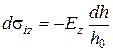 . (108)
. (108)
6. Враховуючи, що 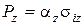 , і рівняння (104) (106), можна записати
, і рівняння (104) (106), можна записати
 ,
,
або
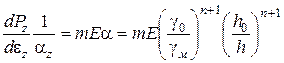 . (109)
. (109)
Вирішуючи спільно рівняння (109) і (107), знаходимо:
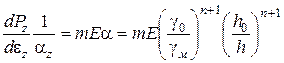 . (110)
. (110)
Отже,
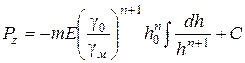 . (111)
. (111)
Проінтегрувавши вираз (111), одержимо
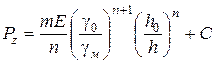 . (112)
. (112)
Аналізуючи вираз, помічаємо, що при  . Тоді
. Тоді
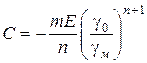 .
.
Підставивши значення постійної інтеграції у вираз (112) одержимо

або
 . (113)
. (113)
Проводячи подальший аналіз, відзначаємо, що при 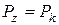 і
і
 ,
,
де 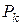 - критичний питомий тиск пресування, відповідне 100%-й густині пресування, рівне напрузі закінчення максимально зміцненого матеріалу, причому для даного металу
- критичний питомий тиск пресування, відповідне 100%-й густині пресування, рівне напрузі закінчення максимально зміцненого матеріалу, причому для даного металу  ;
;  - приведена, або критична, висота пресування, відповідна 100%-й густині.
- приведена, або критична, висота пресування, відповідна 100%-й густині.
Підставивши у вираз (113) значення 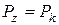 і
і  і вирішуючи його відносно
і вирішуючи його відносно 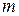 , одержимо
, одержимо
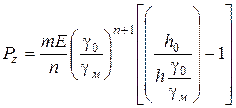 ,
,
звідки
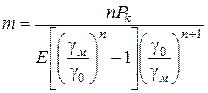 . (114)
. (114)
Далі, підставивши значення в рівняння (113), одержимо:
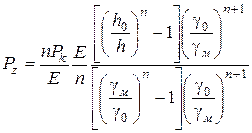 ,
,
або після спрощення
 . (115)
. (115)
Вирішуючи рівняння (115) відносно  , одержуємо
, одержуємо
 . (116)
. (116)
Рівняння (115) і (116) при  є деякими гіперболічними функціями вищого порядку, що відображають кількісні закономірності процесу пресування металевого порошку у всьому інтервалі тиску пресування від
є деякими гіперболічними функціями вищого порядку, що відображають кількісні закономірності процесу пресування металевого порошку у всьому інтервалі тиску пресування від 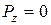 до
до 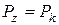 (рис.19).
(рис.19).
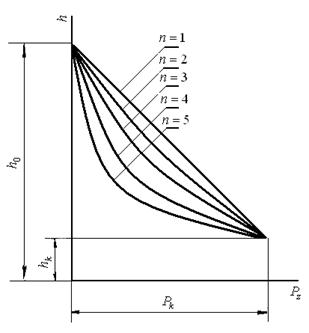
Рисунок 19 - Графічний вид рівняння (116)
Аналіз рівнянь Ждановича показує, що вони справедливі у всьому інтервалі тиску. Проте рівняння було виведене виходячи з припущення, що відсутнє тертя об стінки прес-форми.
Для того, щоб скористатися рівнянням в практиці з урахуванням сил зовнішнього тертя об стінки прес-форми, необхідно мати в своєму розпорядженні закономірність зміни середнього питомого тиску пресування 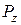 по висоті пресування (функція
по висоті пресування (функція  ).
).
Аналіз напруженого стану ущільнюваного елементу об'єму дозволив Ждановичу одержати цю залежність (рис.20):
 , (117)
, (117)
де 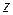 - відстань від дна прес-форми до даного перетину пресування.
- відстань від дна прес-форми до даного перетину пресування.

Рисунок 20 - Графічний вид рівняння (117)
Аналіз рівняння 117 і рис.20 дає можливість дійти висновку, що у будь-який момент пресування тиск нетто рівний середньому питомому тиску на неробочому (нижньому) пуансоні:
 , (118)
, (118)
де 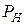 - зусилля, що вимагається для пресування без урахування сил зовнішнього тертя;
- зусилля, що вимагається для пресування без урахування сил зовнішнього тертя;  - загальне необхідне зусилля з урахуванням втрат на зовнішнє тертя.
- загальне необхідне зусилля з урахуванням втрат на зовнішнє тертя.
Враховуючи вираз (117), рівняння пресування можна записати у вигляді
 (119)
(119)
або відносно 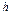
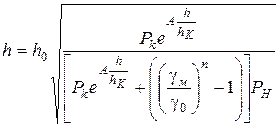 . (120)
. (120)
У рівняннях (119) і (120)
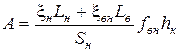 , (121)
, (121)
де  - коефіцієнт бічного тиску відповідно на зовнішню і внутрішню бічну поверхню пресування (додаток
- коефіцієнт бічного тиску відповідно на зовнішню і внутрішню бічну поверхню пресування (додаток 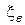 пропадає у разі відсутності останньої);
пропадає у разі відсутності останньої); 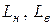 - довжина параметрів або контурів відповідно зовнішньої і внутрішньої бічних поверхонь пресування;
- довжина параметрів або контурів відповідно зовнішньої і внутрішньої бічних поверхонь пресування; 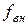 - коефіцієнт зовнішнього тертя пресування об стінки прес-форми;
- коефіцієнт зовнішнього тертя пресування об стінки прес-форми; 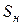 - номінальна площа перетину пресування. Величина
- номінальна площа перетину пресування. Величина 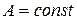 , проте, якщо одна з величин
, проте, якщо одна з величин 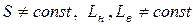 , то і
, то і 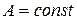 .
.
Для остаточного використання рівнянь (115), (116), (119), (120) необхідно визначити величини 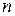 і
і 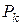 . Показник
. Показник 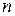 може бути обчислений по (94) або визначений експериментально. Для порошків багатьох металів (
може бути обчислений по (94) або визначений експериментально. Для порошків багатьох металів (  ) він трохи відрізняється від значення 4. У зв'язку з цим при розрахунках можна приймати
) він трохи відрізняється від значення 4. У зв'язку з цим при розрахунках можна приймати  з внесенням при цьому помилки 5-8%. )
з внесенням при цьому помилки 5-8%. )
Величина 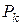 визначається на практиці шляхом пресування дослідних зразків в малогабаритній прес-формі.
визначається на практиці шляхом пресування дослідних зразків в малогабаритній прес-формі.
При цьому використовується вираз (118), звідки
 (122)
(122)
2.4.Рівняння пресування по Бальшину.
При математичному описі процесу пресування, тобто з'ясуванні кількісної закономірності зміни густини порошкового тіла від тиску пресування, часто використовують спрощений підхід, приймаючи при висновку рівнянь пресування певні допущення. Так, при висновку своїх рівнянь М.Ю.Бальшин зробив наступні допущення.
1. Деформація порошкових тіл подібно компактним, тобто якщо зусилля пресування віднести до площі контактного перетину, то межа міцності або межа текучості не залежатиме від пористості і буде однаковою як для пористого, так і для компактного тіла.
2. Деформація частинок підкоряється закону Гука аж до досягнення межі текучості.
3. Контактна поверхня змінюється тільки в результаті пластичної деформації частинок, оскільки при відносно високому тиску пресування приростом контактної поверхні через переміщення частинок один щодо одного можна знехтувати.
4. Наклеп матеріалу частинок, в процесі пресування відсутній, внаслідок чого на контактних ділянках критична напруга (  ) залишається постійним.
) залишається постійним.
Крім того, М.Ю.Бальшин також допускає, що сумарна відносна деформація частинок в контактних ділянках рівна відносній зміні висоти брикета. Приймається також, що площа пресування дорівнює 1 см2 і замість зусилля пресування можна використовувати тиск пресування.
Схема пресування по М.Ю.Балишину показана на рис.21.

Рисунок 21 - Схема пресування по Бальшину
Передбачається, що в циліндровій прес-формі ущільнюється пресування з приведеною висотою  . Під навантаженням Р вона має висоту h. При збільшення тиску на dP висота зменшується на величину dh.
. Під навантаженням Р вона має висоту h. При збільшення тиску на dP висота зменшується на величину dh.
В цьому випадку напруга в порошковому пресуванні визначається розподілом на площу контактного перетину Sk, тобто залежність має такий же вигляд, як і у разі пружної деформації компактного металу, що підкоряється закону Гука:
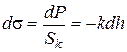 , (123)
, (123)
де  - приріст напруги; dP - приріст навантаження; Sk - площа контактного перетину; kч - постійний коефіцієнт пропорційності у разі відсутності наклепа.
- приріст напруги; dP - приріст навантаження; Sk - площа контактного перетину; kч - постійний коефіцієнт пропорційності у разі відсутності наклепа.
Щоб зробити коефіцієнт k незалежним від розмірів пресування, dh в рівнянні (123) необхідно розділити на первинну, висоту пресування h0. Проте в практичному відношенні деформацію dh зручніше відносити до приведеної висоти hk, тобто до висоти пресування при 100%-й густині.
Враховуючи викладене, а також відповідно до прийнятих допущень замість сумарного тиску P узяти тиск р на одиницю номінального поперечного перетину пресування, рівняння (123) можна записати так:
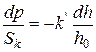 ,
,
або
 , (124)
, (124)
де 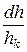 - можна замінити на
- можна замінити на  , оскільки при постійному перетині пресування об'єм змінюється так само, як і її висота;
, оскільки при постійному перетині пресування об'єм змінюється так само, як і її висота; 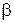 - відносний об'єм пресування.
- відносний об'єм пресування.
Можна записати вираз для  :
:
 , (125)
, (125)
де 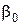 - відносний об'єм насипання порошку;
- відносний об'єм насипання порошку; 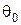 - відносна густина порошку до пресування.
- відносна густина порошку до пресування.
Якщо врахувати, що при ущільненні деформується не весь об'єм, а тільки об'єм, зайнятий порами, то деформацію можна відносити не до початкового і кінцевого об'єму (висоті), а до початкового об'єму пор. В цьому випадку рівняння (124) можна переписати
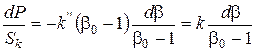 , (126)
, (126)
де  - модуль пресування.
- модуль пресування.
Рівняння (124) незручне тим, що в нього входить контактний перетин
 ,
,
де 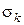 - критична напруга (напруга, при якій починається пластичний перебіг матеріалу).
- критична напруга (напруга, при якій починається пластичний перебіг матеріалу).
Рівняння (126) можна записати так:
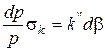
або
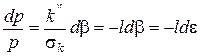 , (127)
, (127)
де  - чинник пресування;
- чинник пресування;  - коефіцієнт пористості, який показує відношення об'єму пор до всього об'єму сипкого тіла (от 0 до
- коефіцієнт пористості, який показує відношення об'єму пор до всього об'єму сипкого тіла (от 0 до 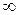 ).
).
Величина 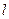 пов'язана з модулем пресування
пов'язана з модулем пресування  таким чином:
таким чином:
 ,
,
або, враховуючи, що  ,
,
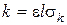
Чинник пресування 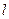 у разі відсутності наклепа - величина постійна, не залежна від тиску, мало залежна від властивостей порошку і найбільш залежна від об'ємних характеристик порошку:
у разі відсутності наклепа - величина постійна, не залежна від тиску, мало залежна від властивостей порошку і найбільш залежна від об'ємних характеристик порошку:
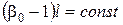 . (128)
. (128)
Слід зазначити, що насправді явище наклепа має дуже велике значення, величини  помітно залежать від тиску і вираз (128) не зовсім точно передає дійсну залежність.
помітно залежать від тиску і вираз (128) не зовсім точно передає дійсну залежність.
Інтегруючи рівняння (127):
 , (129)
, (129)
одержуємо
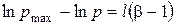
або, переходячи до десяткових логарифмів і враховуючи, що 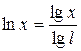 , одержуємо:
, одержуємо:
 (130)
(130)
де 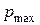 - питомий тиск, відповідний максимальному ступеню ущільнення, коли
- питомий тиск, відповідний максимальному ступеню ущільнення, коли  .
.
Рівняння (130) в координатах  може бути графічно представлене прямою лінією (рис.22, пряма 1)
може бути графічно представлене прямою лінією (рис.22, пряма 1)
Пряма 1 (рис.22) характеризується двома параметрами:
1) 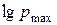 - перетин прямої з віссю ординат;
- перетин прямої з віссю ординат;
2)  - рівний чиннику пресування .
- рівний чиннику пресування .

Рисунок 22 – Ідеалізована (1) і реальна (2) діаграми пресування
по М. Ю. Бальшину
Значення 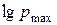 для випадку нетто тиску, тобто за відсутності втрат тиску на тертя, дуже легко визначити. При максимальному ступені ущільнення площа контактного перетину рівна всій площі поперечного перетину, в даному випадку одиниці (оскільки тиску
для випадку нетто тиску, тобто за відсутності втрат тиску на тертя, дуже легко визначити. При максимальному ступені ущільнення площа контактного перетину рівна всій площі поперечного перетину, в даному випадку одиниці (оскільки тиску 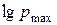 відповідає перетин, рівний одиниці). При цьому
відповідає перетин, рівний одиниці). При цьому 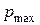 , потрібне для доведення пресування до 100% густини
, потрібне для доведення пресування до 100% густини  , повинне дорівнювати критичній напрузі
, повинне дорівнювати критичній напрузі 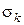 , тобто
, тобто
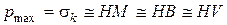
де 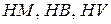 - твердість відповідно по Мейеру, Бринелю, Віккерсу (
- твердість відповідно по Мейеру, Бринелю, Віккерсу ( 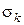 більше на 5-20% ніж
більше на 5-20% ніж  ).
).
Іншими словами, критична напруга, при якій починається пластичний перебіг металу в зоні контакту або руйнування контактних зв'язків (крихка деформація розглядається як випадок пластичної деформації), - величина постійна.
Як вже наголошувалося, чинник пресування за відсутності зміцнення матеріалу - також величина постійна. Насправді це не зовсім так.
Як видно з реальної діаграми пресування (рис.22, 2), 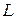 - величина непостійна, і визначається в кожній точці кривої тангенсом кута дотичної до цієї крапки з віссю абсцис. Непостійність
- величина непостійна, і визначається в кожній точці кривої тангенсом кута дотичної до цієї крапки з віссю абсцис. Непостійність 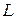 можна пояснити наступним. Чинник пресування
можна пояснити наступним. Чинник пресування 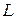 , як випливає з висловленого раніше, пов'язаний з критичною напругою:
, як випливає з висловленого раніше, пов'язаний з критичною напругою:
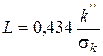 ,
,
де  - приведений модуль пресування, до певної міри аналогічний модуль Юнга (по Бальшину).
- приведений модуль пресування, до певної міри аналогічний модуль Юнга (по Бальшину).
Встановлено, що 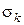 не залишається постійним, а підвищується унаслідок зміцнення металу в процесі пресування.
не залишається постійним, а підвищується унаслідок зміцнення металу в процесі пресування.
Для деяких матеріалів в певному інтервалі тиску цією зміною можна нехтувати, а в інших випадках зміни 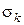 і
і 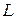 настільки великі навіть в невеликих інтервалах зміни тиску пресування, що в практичних цілях рівняння (130) використати неможливо.
настільки великі навіть в невеликих інтервалах зміни тиску пресування, що в практичних цілях рівняння (130) використати неможливо.
Бальшин відзначає, що спроби дати рівняння пресування з постійним коефіцієнтом 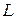 для всіх порошків і у всіх інтервалах тиску приречені на невдачу.
для всіх порошків і у всіх інтервалах тиску приречені на невдачу.
Проте для більшості металів середньої твердості (наприклад, мідь, залізо) чинник пресування 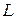 може бути з достатньою для практики точністю виражений в диференціальному рівнянні:
може бути з достатньою для практики точністю виражений в диференціальному рівнянні:
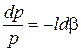
у вигляді наступної функції:
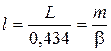 , (131)
, (131)
де 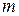 - показник пресування, приблизно постійний в значному інтервалі тиску.
- показник пресування, приблизно постійний в значному інтервалі тиску.
Підставивши вираз (131) в рівняння (129), одержимо:
 . (132)
. (132)
Інтегруючи це рівняння, одержуємо:
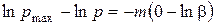 ;
;
 (133)
(133)
або після потенціювання
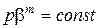 (134)
(134)
одержуємо друге рівняння Бальшина.
Рівняння (134) можна представити так:
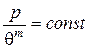 . (135)
. (135)
якщо врахувати, що 
Логарифмуючи рівняння (134) і (135), одержуємо:
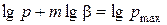 ; (136)
; (136)
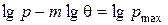 . (137)
. (137)
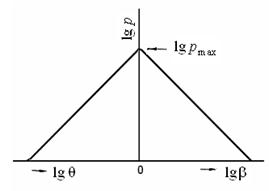
Рисунок 23 - Графічний вид рівнянь (136) і (137)
Рівняння (136) і (137) в графічному вигляді мають вид прямих, показаних на рис.23.
Тангенс кута нахилу прямих до осі абсцис визначає показник  , а відрізок, прямий, що відсікається, від осі ординат, рівний логарифму максимального питомого тиску пресування (у ідеальному випадку за відсутності втрат на тертя в прес-формі
, а відрізок, прямий, що відсікається, від осі ординат, рівний логарифму максимального питомого тиску пресування (у ідеальному випадку за відсутності втрат на тертя в прес-формі  ).
).

Рисунок 24 - Реальні діаграми пресування
На практиці діаграми  в деяких випадках відрізняються від прямолінійності (рис. 24).
в деяких випадках відрізняються від прямолінійності (рис. 24).
Якщо крива має вигин опуклості вниз (  зростає швидше), то в процесі пресування
зростає швидше), то в процесі пресування 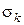 не залишається постійним, а росте із збільшенням тиску пресування.
не залишається постійним, а росте із збільшенням тиску пресування.
Слід мати на увазі, що вказане явище спостерігається не тільки унаслідок підвищення твердості контактних ділянок за рахунок зміцнення (по Бальшину), але і ще з двох причин:
1) унаслідок збільшення ефекту тертя між частинками, який гальмує деформацію частинок при їх взаємному стисненні (у зв'язку із збільшенням розмірів контактних ділянок);
2) унаслідок посилення об'ємних напружень, що накопичуються в частинках у міру їх деформації.
У разі, коли крива  має опуклість вгору (сповільнюється в зростанні
має опуклість вгору (сповільнюється в зростанні  ), зовнішні шари частинок виявляються твердішими (через окиснення, зміцнення або яких-небудь інших причин).
), зовнішні шари частинок виявляються твердішими (через окиснення, зміцнення або яких-небудь інших причин).
Властивості частинок (форма, розмір, насипна щільність ) не впливають на 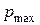 . Останнє завжди, рівно тиску закінчення і залежить від хімічного складу порошку.
. Останнє завжди, рівно тиску закінчення і залежить від хімічного складу порошку.
При отриманні пресувань з густиною менше 100% властивості порошків сильно впливають на тиск пресування, необхідний для досягнення певної густини пресування з причин, розглянутих раніше.
На закінчення можна сказати, що, на думку Ждановича, логарифмічні і напівлогарифмічні рівняння пресування Бальшина, виведені з фізичних передумов, лише приблизно відображають суть процесу в цілому, маючи достатню точність при постійних значеннях коефіцієнтів і показників тільки в обмеженому діапазоні тиску.
2.5. Рівняння пресування по Куніну і Юрченко
Серед рівнянь пресування, приведених різними авторами, багато одержаних емпірично тобто шляхом математичної обробки експериментальних даних. В цьому відношенні є типовим рівняння по Н.Ф.Куніну і В.Д.Юрченко.
Своє рівняння пресування автори одержали математичною обробкою експериментальних даних, отриманих при ущільненні пластичних і крихких порошків ( 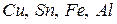 , графіту, селітри, кам'яної солі і ін.) Побудовані залежності
, графіту, селітри, кам'яної солі і ін.) Побудовані залежності
Читайте також:
- II. Основні закономірності ходу і розгалуження судин великого і малого кіл кровообігу
- II. Основні засоби
- II.3. Основні способи і прийоми досягнення адекватності
- А .Маршалл - основоположник неокласичної теорії.
- Автокореляція залишків – це залежність між послідовними значеннями стохастичної складової моделі.
- Адвокатура в Україні: основні завдання і функції
- Аксіоматичний метод у математиці та суть аксіоматичної побудови теорії.
- Альтернативні теорії вартості
- Альтернативні теорії вартості
- Альтернативні теорії вартості
- Альтернативні теорії капіталу
- Альтернативні теорії макроекономічного регулювання
| <== попередня сторінка | | | наступна сторінка ==> |
| ПРЕСУВАННЯ | | | ПРАКТИКА ПРЕСУВАННЯ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |