Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Алгоритм у Mathcad

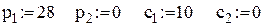
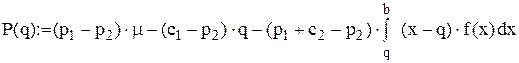
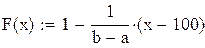
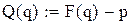
Оптимальний обсяг поставки

або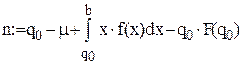

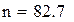
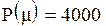
Коментар. Оскільки і , то середня кількість нерозпроданих за свята фігурок при умові, що до початку періоду їх було замовлено 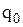штук дорівнює 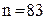штуки. Середній прибуток складає 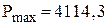грош. од. і 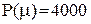грош. од.

Результати розрахунків показують, що виручка у першому випадку, коли замовляється батонів дорівнює грош. од. і помітно відрізняється від виручки грош. од., одержуваної при замовленні батонів.

Таким чином, якщо розмір замовлення на 29 одиниць перевищує середній обсяг попиту, то це приводить до збільшення прибутку на 114,3 грош. од. Але слід звернути увагу на те, що середня кількість нереалізованих одиниць товару може складати 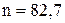одиниць. ▲

Приклад 3.14. Одночасно з випуском літаків виготовляються і деякі запасні частини до них. Після того, як збірка літака закінчена, вже важко дістати до нього додаткові запасні частини. Після закінчення збірки літака треба визначити, скільки запасних частин певного типу слід мати у комплекті до нього. Припускається, що попит на запасні частини цього типу невеликий і розподілений за законом Пуассона, а інтенсивність попиту (на основі накопиченого досвіду) складає 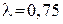одиниць у рік. Розподіл терміну експлуатації літака точно невідомий. Припускається, що він може бути описаний гама-розподілом із середнім років і середнім квадратичним відхиленням роки. Кожна запасна частина розглядуваного типу коштує 10000 грош. од., а якщо до моменту виходу із ладу всього літака які-небудь запасні частини залишаються не використаними, то кожна із них коштує всього лише 500 грош. од. Якщо усі запасні частини комплекту витрачені, то для того, щоб дістати ще один запасний блок, необхідно витратити 26000 грош. од.

Щоб визначити, скільки запасних частин повинно бути у комплекті до літака, необхідно спочатку знайти безумовний розподіл величини попиту за час експлуатації літака. Оскільки попит на запасні частини розподілений за законом Пуассона, а термін експлуатації літака має гама-розподіл, то безумовний розподіл величини попиту представляється від’ємним біноміальним розподілом зі щільністю імовірності

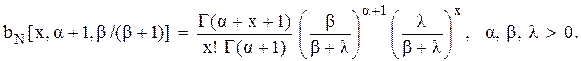
Для визначення 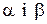використаємо співвідношення

які зв’язують 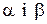із середнім значенням 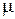і середнім квадратичним відхиленням 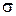для гама-розподілу.

Функція від’ємного біноміального розподілу визначається співвідношенням

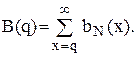
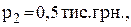
Із наведених даних видно, що і Максимізація прибутку при 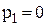еквівалентна мінімізації середніх витрат. Отже, у цьому випадку застосовується формула аналогічна (3.18).

Таким чином, математичне сподівання функції витрат дорівнює

Якщо q означає кількість запасних частин у комплекті, то оптимальне значення яке мінімізує середні витрати G(q), дорівнює найбільшому q, для якого виконується умова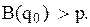

Цю умову можна представити у вигляді

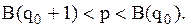
Середній попит на запасні частини за час експлуатації літака (6 років) дорівнює одиниць. Якщо у комплекті до літака є q запасних частин, то середня кількість запасних частин, не використаних до моменту зняття літака з експлуатації, дорівнює

Для знайденого оптимального значення 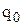визначаємо середню кількість невикористаних запасних частин 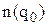і мінімальне значення функції витрат

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Алгоритм у Mathcad	\|	Алгоритм реалізації моделі

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.006 сек.