• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Модель системи з залежними від часу витратами

У попередній моделі управління запасамирозглядались постійні, не залежні від часу витрати. Узагальнимо цю модель, ввівши витрати утримання запасів і втрати від дефіциту як функції часу, пропорційні відповідно терміну їх зберігання і часу між моментом надходження незадовільненої вимоги і кінцем періоду 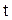, тобто пропорційні часу тривалості дефіциту.

Отже введемо додаткові величини:

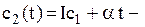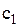витрати, пов’язані із зберіганням одиниці запасів на момент часу , де – ціна запасів; І – коефіцієнт пропорційності, який називається коефіцієнтом витрат збереження запасів (він має розмірність – вартість в одиницю часу на одиницю капіталу, вкладеного у запаси); коефіцієнт пропорційності часу зберігання запасу;

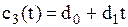– втрати від дефіциту на момент часу (вартісний коефіцієнт питомої нестачі запасу), де – постійна величина, – втрати пропорційні часу наявності дефіциту.

Розглянемо модель для випадку попиту, розподіленого за законом Пуассона

де – параметр розподілу, який дорівнює середньому значенню попиту на інтервалі часу t.

Припустимо, що середня інтенсивність попиту 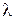постійна, а тривалість періоду Т фіксована і невипадкова. Тоді, якщо на початку періоду на складі є s одиниць запасу, то середній очікуваний доход системи від реалізації товару за основною ціною і реалізації залишку по ціні 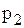за період T у залежності від попиту дорівнюватиме

(3.41)

Визначивши витрати на зберігання запасу і втрати від дефіциту за період як

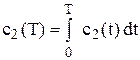і ,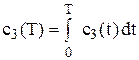

одержимо сумарні витрати на придбання товару (створення запасу), його зберігання та втрати від дефіциту

(3.42)

Прибуток системи управління запасами за період буде дорівнювати різниці між доходом та витратами і складе

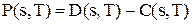(3.43

Перетворимо цей вираз, обчисливши математичне сподівання попиту у періоді та переходячи до функції 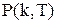, одержимо вираз:

(3.44)

.

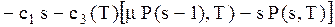
Для знаходження оптимального рівня наявних запасів 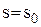, який максимізує очікуваний прибуток системи 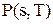, розглянемо величину яка у економічних термінах представляє собою приріст прибутку, пов’язаного із зміною рівня наявних запасів від величини 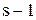до s. Подальше підвищення цього рівня доцільне до тих пір, поки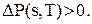

Маємо

(3.45)

.

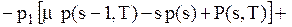
Найбільше s, для якого 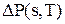додатне, буде оптимальним значенням запасу, який повинен бути на складі. Отже оптимальне значення 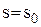повинно задовольняти умові

. (3.46)

Слід правильно інтерпретувати витрати, пов’язані з дефіцитом запасів. Джерело таких витрат, звичайно, полягає у тому, що якщо, наприклад, розглядати запасні деталі до устаткування, яке використовується у випуску продукції, то 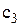представляє інтенсивність зменшення продуктивності у наслідок простоїв устаткування, пов’язаних з відсутністю запасних деталей протягом періоду.

У деяких випадках час закінчення періоду, який співпадає з моментом повного зносу устаткування, неможливо передбачити точно, тоді його треба описувати певним імовірнісним розподілом.

Для більш докладного аналізу даної системи управління запасами інтерес можуть представляти наступні характеристики:

Ø середня кількість реалізованих одиниць запасу за період Т

;

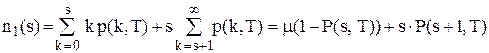Ø середній доход від реалізації запасу (гр. одиниць)

Ø середня кількість нереалізованого за час T запасу (залишок запасу на кінець періоду), який дорівнює різниці між рівнем запасу на початку періоду і кількістю реалізованого запасу

;

Ø середній доход від продажу залишку запасу (у гр. одиницях)

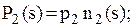
Ø середні витрати на створення запасу

Ø середні витрати на зберігання запасу (у гр.. одиницях)

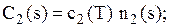
Ø якщо до моменту часу T попит досяг рівня , то середня величина дефіциту за період T складає

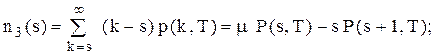
Ø середні втрати від дефіциту дорівнюють (у гр. одиницях)

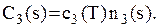
Часто важко обґрунтувати вибір певного розподілу ймовірностей. У цьому випадку краще всього задати n різних значень T_i, приписавши кожному з них імовірність 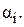Тоді якщо на початку періоду на складі було s одиниць запасу, а середній прибуток за період тривалістю 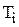дорівнює то усереднений по всім можливим значенням 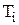прибуток складе

(3.47)

Треба знайти s, яке максимізує вираз 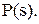Цим s буде найбільше 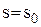, для якого вираз

(3.48)

додатний. Кожне має вигляд (3.37), у якому T замінюється на 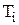. У порівнянні з попереднім випадком задача визначення значно ускладнюється.

Приклад 3.15. Автотранспортна фірма закуповує двигуни до імпортних автобусів. Попит на двигуни випадковий і описується розподілом Пуассона із середнім значенням 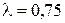одиниць на рік. Закупівельна вартість двигуна дорівнює тис. доларів. Щорічний прибуток від експлуатації двигуна складає тис. доларів. Відомо, що через 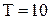років зберігання вартість кожного двигуна у наслідок старіння (фізичного чи морального) знижується до 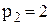тис. доларів. 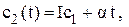Витрати, пов’язані із зберіганням одного двигуна протягом часу є функцією часу і дорівнюють де 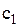– ціна запасного двигуна, І – коефіцієнт вартості витрат на збереження запасів в одиницю часу на одиницю капіталу, вкладеного у запаси, коефіцієнт пропорційності часу зберігання запасу. 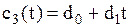Втрати, пов’язані із дефіцитом двигуна є функцією часу і дорівнюють , де 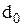– постійна величина, 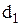– втрати пропорційні часу наявності дефіциту. Автобус повинен пропрацювати 10 років. Двигуни можуть бути замовлені тільки одночасно із закупівлею автобусів.

Визначимо, скільки запасних двигунів 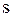повинна закупити фірма, щоб очікуваний прибуток від експлуатації автобусів був максимальний.

Читайте також:

1. G2G-модель електронного уряду
2. I. Органи і системи, що забезпечують функцію виділення
3. I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
4. II. Анатомічний склад лімфатичної системи
5. IV. Розподіл нервової системи
6. IV. Система зв’язків всередині центральної нервової системи
7. IV. Філогенез кровоносної системи
8. OSI - Базова Еталонна модель взаємодії відкритих систем
9. POS-системи
10. T. Сутність, етіологія та патогенез порушень опорно-рухової системи
11. VI. Філогенез нервової системи
12. А) Заробітна плата її форми та системи.

Переглядів: 613