
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Алгоритм у Mathcad
Значення вартісних показників
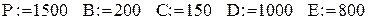
Параметри розподілів попиту і масиви значень цих розподілів

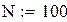
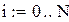
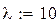

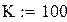
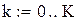
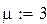

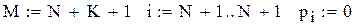


Коефіцієнти цільової функції
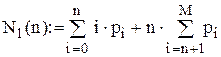
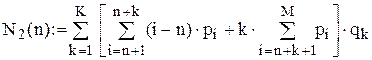
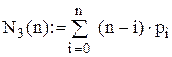
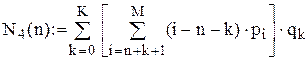
Цільова функція F(n)
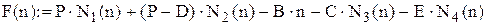
Максимум цільової функції F(n) – максимальний доход фірми
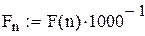

Оптимальне значення кількості автомобілів
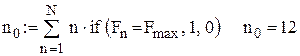
Функція прибутку

Функція витрат

Значення цільової функції F, прибутку  і витрат
і витрат 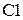



Одержана оптимальна кількість автомобілів n0 дає можливість визначити також операційні характеристики системи для оптимального плану.
Ø кількість зайнятих автомобілів
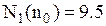
Ø кількість допоміжних автомобілів
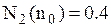
Ø кількість невикористаних власних автомобілів
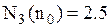
Ø кількість недостатніх автомобілів (дефіцит)
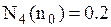
Імовірності станів системи:
Ø використовуються основні автомобілі

Ø використовуються допоміжні автомобілі

Ø основних і допоміжних автомобілів недостатньо (дефіцит)
Графік цільової функції і її складових для n := 4 . . 20

Рис. 3.7. Графік цільової функції Fn і її складових 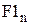 і
і 
Коментар. Одержані результати розрахунків показують, що при пуассонівських розподілах попиту і пропозиції додаткових автомобілів із середніми значеннями 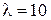 і
і 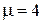 , оптимальна кількість постійних автомобілів буде дорівнювати n0=12. При цьому середня кількість зайнятих автомобілів дорівнюватиме
, оптимальна кількість постійних автомобілів буде дорівнювати n0=12. При цьому середня кількість зайнятих автомобілів дорівнюватиме 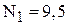 одиниць, середня кількість допоміжних –
одиниць, середня кількість допоміжних – 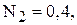 середня кількість незайнятих власних
середня кількість незайнятих власних  , середня кількість дефіциту автомобілів –
, середня кількість дефіциту автомобілів – 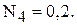 Імовірності цих станів відповідно дорівнюють
Імовірності цих станів відповідно дорівнюють 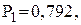
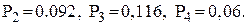
Як видно із таблиці значень функції 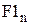 , величина прибутку для кількості автомобілів
, величина прибутку для кількості автомобілів  стає незмінною. Це є наслідком того, що при цих значеннях n попит на автомобілі повністю задовольняється, в результаті чого зайві автомобілі не дають прибутку. Витрати ж на їх утримання
стає незмінною. Це є наслідком того, що при цих значеннях n попит на автомобілі повністю задовольняється, в результаті чого зайві автомобілі не дають прибутку. Витрати ж на їх утримання  постійно зростають. ▲
постійно зростають. ▲
Контрольні запитання
1. Якою характеристикою описується попит у стохастичних моделях управління запасами.
2. Чим пояснюється необхідність створювати резервний запас у системах управління запасами з випадковим попитом.
3. Чи приводить до збитків надлишок запасу у системі управління запасами із випадковим попитом.
4. Якій умові задовольняє оптимальний рівень запасів у системі управління запасами із випадковим попитом з урахуванням збитків від надлишку або нестачі товару.
5. Якій умові задовольняє оптимальний рівень запасів у системі з витратами на зберігання запасу і зі збитками від незадоволеного попиту при неперервно розподіленому попиті.
6. Дати означення  -моделі системи управління запасами з двома рівнями.
-моделі системи управління запасами з двома рівнями.
7. У якому випадку у одноетапній моделі системи управління запасами з двома рівнями (стратегія  може виявитись оптимальним не поповнювати запас до рівня
може виявитись оптимальним не поповнювати запас до рівня  .
.
8. Чи вірно, що у моделі системи управління запасами при миттєвому попиті і при обліку витрат на оформлення замовлення, оптимальний розмір замовлення співпадає з розміром замовлення у системі без врахування витрат.
9. За якими умовами у моделі системи управління запасами з врахуванням витрат на оформлення замовлення визначається оптимальна кількість продукції 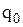 , яку слід замовляти, якщо перед замовленням є z одиниць запасу і нижній рівень запасу дорівнює
, яку слід замовляти, якщо перед замовленням є z одиниць запасу і нижній рівень запасу дорівнює 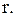
10. Чи є випливає оптимальність 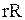 -стратегії із того, що функція витрат вгнута.
-стратегії із того, що функція витрат вгнута.
11. Який вигляд має критерій оптимальності в загальній моделі управління запасами у одному періоді.
12. Якій умові задовольняє точка  , яка є точкою максимуму функції прибутку у загальній моделі управління запасами в одному періоді.
, яка є точкою максимуму функції прибутку у загальній моделі управління запасами в одному періоді.
13. Із якого рівняння визначається оптимальний обсяг поповнення запасу 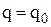 у загальній моделі управління запасами в одному періоді.
у загальній моделі управління запасами в одному періоді.
17. Чи вірно, що в загальній неперервній моделі управління запасами в одному періоді математичне сподівання прибутку як функція від  має абсолютний максимум, якщо вона є строго опуклою функцією.
має абсолютний максимум, якщо вона є строго опуклою функцією.
18. Якій умові задовольняє оптимальне значення запасу, який повинен бути на складі у моделі системи управління запасами в одному періоді з витратами, залежними від часу
Задачі
3.1. Загальний обсяг замовлень товару торгівельною фірмою у квартал (період T днів) дорівнює 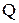 одиниць. Товари замовляються раз у квартал і постачаються на склад фірми партіями однакового обсягу, вказаному в замовленні. Постачання відбувається на початку кожного кварталу. Витрати на постачання однієї партії складають
одиниць. Товари замовляються раз у квартал і постачаються на склад фірми партіями однакового обсягу, вказаному в замовленні. Постачання відбувається на початку кожного кварталу. Витрати на постачання однієї партії складають 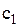 грн., а витрати зберігання одиниці запасу за добу
грн., а витрати зберігання одиниці запасу за добу 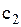 грн. Дефіцит товару недопустимий. Визначити оптимальну стратегію управління запасами у даній системі:
грн. Дефіцит товару недопустимий. Визначити оптимальну стратегію управління запасами у даній системі:
Ø оптимальній обсяг замовлень  ;
;
Ø середню кількість замовлень у квартал  ;
;
Ø середній інтервал між послідовними замовленнями 
Ø мінімальні середні витрати системи у квартал.
Визначити ці ж параметри системи, а також величину резервного запасу 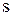 і точку замовлення замовлення
і точку замовлення замовлення 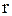 при умові, що імовірність вичерпання запасу не перевищує
при умові, що імовірність вичерпання запасу не перевищує  денний попит є нормально розподіленою випадковою величиною з математичнім сподіванням
денний попит є нормально розподіленою випадковою величиною з математичнім сподіванням 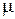 одиниць у день і середнім квадратичним відхиленням
одиниць у день і середнім квадратичним відхиленням  одиниці, тобто має розподіл
одиниці, тобто має розподіл 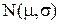 .
.
Розглянути також випадок, коли термін виконання замовлення від моменту його подачі до реальної поставки складає 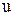 днів.
днів.
Параметри моделі:

3.2. Музичний магазин продає популярні компакт-диски. Розподіл денного попиту на диски можна апроксимувати нормальним розподілом з математичним сподіванням 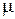 дисків і стандартним відхиленням
дисків і стандартним відхиленням 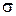 дисків. Вартість зберігання диску в магазині складає
дисків. Вартість зберігання диску в магазині складає 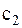 грн. в день. Розміщення нового замовлення обходиться магазину у
грн. в день. Розміщення нового замовлення обходиться магазину у  грн. Постачальник зазвичай встановлює термін виконання замовлення в
грн. Постачальник зазвичай встановлює термін виконання замовлення в 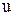 днів. Припустимо, що магазин хоче обмежити ймовірність вичерпання запасу дисків протягом терміну виконання замовлення величиною, яка не перевищує
днів. Припустимо, що магазин хоче обмежити ймовірність вичерпання запасу дисків протягом терміну виконання замовлення величиною, яка не перевищує 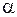 .
.
Визначити оптимальну стратегію управління запасами для магазина:
Ø оптимальний обсяг замовлення;
Ø оптимальну кількість поставок і інтервал часу між поставками;
Ø мінімальні витрати;
Ø величину резервного запасу і точку замовлення.
Параметри моделі:

3.3. Туристична фірма обслуговує клієнтів, маючи у своєму розпорядженні s власних автобусів. Якщо у якийсь день попит на k автобусів нижче кількості наявних автобусів s, то незайняті автобуси використовуються на перевезеннях пасажирів на міських маршрутах, при цьому фірма втрачає прибуток у  грн. на один автобус. Якщо попит k вище кількості автобусів s, то для обслуговування клієнтів у фірми виникає необхідність у оренді додаткових автобусів, що веде до збитків у розмірі
грн. на один автобус. Якщо попит k вище кількості автобусів s, то для обслуговування клієнтів у фірми виникає необхідність у оренді додаткових автобусів, що веде до збитків у розмірі 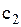 грн. на один автобус.
грн. на один автобус.
Розв’язати задачу для трьох умов відносно попиту, вираженого у кількості автобусів:
1. Попит є дискретна випадкова величина X, задана рядом розподілу 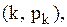 .
. 
| k | Σ | |||||||||||
| pk | 0,0 | 0,01 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,17 | 0,04 | 0,02 | 0,01 |
2. Попит є неперервною величиною, розподіленою за експоненціальним законом із щільністю розподілу 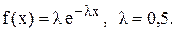
3. Попит є неперервною величиною, розподіленою за нормальним законом з параметрами 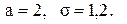
Визначити оптимальну стратегію управління запасами:
Ø оптимальну кількість автобусів s, яку повинна мати фірма щоденно, щоб можливі втрати прибутку були мінімальні;
Øвтрати від нестачі автобусів (збитки від незадоволеного попиту); залежність загальних витрат від втрат у наслідок дефіциту; залежність економічної функції (математичного сподівання втрат) від величини збитку 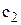 у наслідок дефіциту автобусів.
у наслідок дефіциту автобусів.
Показники витрат: 
3.4. Автотранспортна фірма зберігає запасні деталі на складі і витрачає їх рівномірно протягом дня. Витрати на зберігання однієї деталі на складі дорівнюють  грн., штраф за дефіцит деталі обходиться у
грн., штраф за дефіцит деталі обходиться у 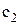 грн.
грн.
Розв’язати задачу для трьох умов відносно попиту на запасні деталі:
1. Попит є дискретна випадкова величина X, задана рядом розподілу 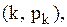 .
. 
| k | Σ | |||||||||||
| pk | 0,00 | 0,01 | 0,05 | 0,10 | 0,15 | 0,22 | 0,25 | 0,15 | 0,04 | 0,02 | 0,01 |
2. Попит є неперервною величиною, розподіленою за експоненціальним законом із щільністю розподілу  при
при  ;
;
3. Попит є неперервною величиною, розподіленою за нормальним законом з параметрами 
Визначити оптимальну стратегію управління запасами: оптимальний щоденний запас деталей на складі такий, щоб можливі витрати на їх зберігання і збитки від дефіциту були мінімальні.
Показники витрат 
3.5. Станція технічного обслуговування автомобілів виконує заміну шин і витрачає їх у кількості Q одиниць у місяць. Замовлення на нову поставку шин обходиться станції у  грн. Вартість зберігання однієї шини протягом місяця дорівнює
грн. Вартість зберігання однієї шини протягом місяця дорівнює 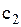 грн., а питомі втрати від дефіциту –
грн., а питомі втрати від дефіциту – 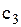 грн. Статистичні дані свідчать про те, що попит у період поставки є випадковою величиною, рівномірно розподіленою у інтервалі
грн. Статистичні дані свідчать про те, що попит у період поставки є випадковою величиною, рівномірно розподіленою у інтервалі  , де а=200.
, де а=200.
Визначити оптимальну стратегію управління запасами:
Ø оптимальний обсяг поставки і оптимальний щоденний запас шин на складі такі, щоб можливі витрати на їх зберігання і збитки від дефіциту були б мінімальні;
Ø кількість замовлень і інтервал часу між послідовними замовленнями.
Параметри моделі: 
3.6. Фірма закуповує імпортні комп’ютери і комплекти запчастин до них. Протягом терміну експлуатації комп’ютерів деталі зберігаються на складі фірми і витрачаються у відповідності з попитом на них. Нестача запасних деталей у разі їх потреби призводить до певних збитків у наслідок виходу комп’ютерів із ладу. Витрати на закупівлю одного комплекту деталей дорівнюють 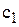 , середні витрати на зберігання їх на складі протягом періоду –
, середні витрати на зберігання їх на складі протягом періоду – 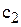 , втрати від дефіциту у наслідок простою комп’ютерів дорівнюють
, втрати від дефіциту у наслідок простою комп’ютерів дорівнюють 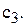
Попит за період (наприклад, 10 років) описується одним із наступних імовірнісних розподілів:
1. Нормальним розподілом з математичним сподіванням a = 5 і стандартним відхилення 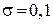 комплектів.
комплектів.
2. Рівномірним розподілом із щільністю ймовірності f(x) = 1/(b–a), де  – границі розподілу кількості комплектів.
– границі розподілу кількості комплектів.
3. Дискретним розподілом  , заданим у таблиці
, заданим у таблиці
| k | ||||||||||

| 0.01 | 0.02 | 0.07 | 0.12 | 0.17 | 0.24 | 0.22 | 0.12 | 0.03 | 0.01 |
Визначити оптимальну стратегію управління запасами:
Ø оптимальний запас запасних частин, щоб можливі витрати на їх зберігання і збитки від дефіциту були мінімальні;
Ø мінімальні витрати на створення і утримання запасу.
Показники витрат 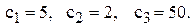
3.7. Розглянемо систему управління запасами, описану у попередній задачі, але припустимо, що попит задовольняється не миттєво, а рівномірно протягом періоду. Припустимо також, що попит розподілений за рівномірним законом із щільністю ймовірності 
Визначити оптимальну стратегію управління запасами:
Ø оптимальний запас запасних частин, щоб можливі витрати на їх зберігання і збитки від дефіциту були б мінімальні;
Ø мінімальні витрати на створення і утримання запасу.
Параметри моделі: 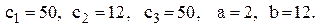
3.8. Щоденний попит на продукцію протягом одного періоду задовольняється миттєво на початку періоду. Попит є випадковою величиною, рівномірно розподіленою на інтервалі від 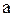 до
до  одиниць. Вартість подачі замовлення дорівнює
одиниць. Вартість подачі замовлення дорівнює  грн., вартість одиниці продукції –
грн., вартість одиниці продукції – 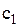 грн. Вартість зберігання одиниці продукції протягом періоду дорівнює
грн. Вартість зберігання одиниці продукції протягом періоду дорівнює 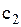 грн., а штраф за дефіцит одиниці продукції –
грн., а штраф за дефіцит одиниці продукції – 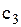 грн. Початковий запас дорівнює
грн. Початковий запас дорівнює  одиницям.
одиницям.
Визначити оптимальну стратегію управління запасами: оптимальний обсяг замовлення 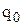 і нижній рівень запасу
і нижній рівень запасу  .
.
Параметри моделі: 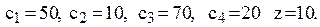
3.9. У великому продовольчому магазині необхідно визначити, скільки пакетів молочних продуктів потрібно замовляти на день. Вивчення продажу цих продуктів показало, що попит у день можна вважати випадковою величиною, розподіленою за нормальним законом із середнім 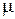 і середнім квадратичним відхиленням
і середнім квадратичним відхиленням 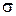 . Один пакет продається за
. Один пакет продається за 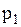 грн. Собівартість товару для магазину складає
грн. Собівартість товару для магазину складає  грн. за пакет. Усі непродані пакети збуваються після закінчення строку придатності по ціні
грн. за пакет. Усі непродані пакети збуваються після закінчення строку придатності по ціні  грн. за пакет.
грн. за пакет.
Визначити оптимальну стратегію управління запасами:
Øоптимальний розмір закупівлі молочних продуктів, який максимізує середній прибуток;
Øсередню кількість непроданих пакетів;
Øмаксимальне значення прибутку;
Øпорівняти денну виручку для випадку, коли у день закуповується оптимальна кількість молочних продуктів із середньою виручкою, коли у день закуповується така кількість, яка дорівнює середньому попиту.
Параметри моделі: 
3.10. Створення запасу товару у магазині протягом тижня здійснюється миттєво на його початку. Щоденний попит на товар є випадковою величиною, розподіленою за нормальним законом із середнім  і середнім квадратичним відхиленням
і середнім квадратичним відхиленням 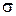 . Одиниця товару продається за
. Одиниця товару продається за  грн. Собівартість одиниці товару для магазину складає
грн. Собівартість одиниці товару для магазину складає 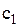 грн. Усі непродані товари збувається після закінчення строку придатності по ціні
грн. Усі непродані товари збувається після закінчення строку придатності по ціні  грн. за одиницю. При неспроможності задовольнити попит покупців магазин несе збитки, пов’язані із втратою очікуваного прибутку. Ці збитки оцінюються у розмірі
грн. за одиницю. При неспроможності задовольнити попит покупців магазин несе збитки, пов’язані із втратою очікуваного прибутку. Ці збитки оцінюються у розмірі 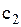 грн. за одиницю товару.
грн. за одиницю товару.
Визначити оптимальну стратегію управління запасами:
Ø оптимальну кількість закупівлі товару, яка максимізує середній прибуток;
Ø середню кількість непроданих пакетів;
Ø максимальний прибуток.
Параметри моделі:
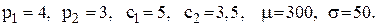
3.11. До курортного сезону універсальний магазин повинен закупити партію дорогих шкіряних сумок. Кожна сумка коштує магазину 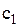 грн., а продається за
грн., а продається за 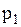 грн. Припускається, що усі нереалізовані у сезон сумки можуть бути продані за попередньою ціною. Тим не менш 30 % коштів, вкладених у нереалізовані вчасно сумки, “заморожуються”, оскільки, використавши ці кошти інакше, можливо одержати більший прибуток. Припускається, що за сезон вдасться продати від
грн. Припускається, що усі нереалізовані у сезон сумки можуть бути продані за попередньою ціною. Тим не менш 30 % коштів, вкладених у нереалізовані вчасно сумки, “заморожуються”, оскільки, використавши ці кошти інакше, можливо одержати більший прибуток. Припускається, що за сезон вдасться продати від 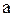 до
до  сумок, причому продаж будь-якої кількості у вказаних межах рівноімовірний. Додаткові дослідження показали, що більш точно попит виражається нормальним розподілом із середнім
сумок, причому продаж будь-якої кількості у вказаних межах рівноімовірний. Додаткові дослідження показали, що більш точно попит виражається нормальним розподілом із середнім  і середнім квадратичним відхиленням
і середнім квадратичним відхиленням 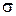 сумок.
сумок.
Визначити оптимальну стратегію управління запасами:
Øоптимальну кількість сумок, яку слід закупити;
Øщо дасть магазину додаткова інформація про попит.
Параметри моделі:

3.12. Автозаправна станція замовляє бензин у фірми, яка обслуговує декілька АЗС. Власник АЗС повинен вирішити, скільки йому слід замовляти бензину на місяць. Замовлення потрібне не пізніше, ніж за  тижнів до дня поставки. Кожний літр бензину обходиться АЗС у
тижнів до дня поставки. Кожний літр бензину обходиться АЗС у  грн., а продається за
грн., а продається за 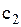 грн. за літр. Сума, витрачена на нереалізований за місяць бензин, складає платіжний дефіцит. Можна стверджувати, що за місяць АЗС напевно вдасться продати не менше
грн. за літр. Сума, витрачена на нереалізований за місяць бензин, складає платіжний дефіцит. Можна стверджувати, що за місяць АЗС напевно вдасться продати не менше 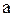 тис. літрів бензину, але не більше
тис. літрів бензину, але не більше  тис. літрів. Продаж будь-якої кількості між
тис. літрів. Продаж будь-якої кількості між 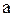 і
і  тис. літрів вважаються рівноімовірними подіями, тобто АЗС припускає, що обсяг попиту рівномірно розподілений на інтервалі від
тис. літрів вважаються рівноімовірними подіями, тобто АЗС припускає, що обсяг попиту рівномірно розподілений на інтервалі від 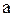 до
до  тис. літрів.
тис. літрів.
Визначити оптимальну стратегію управління запасами: оптимальний обсяг замовлення бензину і прибуток, який може одержати АЗС.
Параметри моделі:
3.13. Торгівельна фірма постачає автомобілі представницького класу. Одночасно з випуском автомобілів виготовляються і деякі запасні частини до них. Після того, як збірка автомобіля закінчена, вже важко дістати до нього додаткові запасні частини. Треба визначити, скільки запасних частин певного типу слід мати у комплекті до автомобіля, який замовляє фірма. Припускається, що попит на запасні частини невеликий і розподілений за законом Пуассона, а інтенсивність попиту (на основі накопиченого досвіду) складає  одиниць у рік. Розподіл терміну експлуатації літака точно невідомий. Припускається, що він може бути описаний гама-розподілом із середнім
одиниць у рік. Розподіл терміну експлуатації літака точно невідомий. Припускається, що він може бути описаний гама-розподілом із середнім  років і середнім квадратичним відхиленням
років і середнім квадратичним відхиленням  років. Кожна запасна частина розглядуваного типу коштує у середньому
років. Кожна запасна частина розглядуваного типу коштує у середньому  грн., а якщо до моменту виходу із ладу всього автомобіля які-небудь запасні частини залишаються не використаними, то кожна із них коштує всього лише
грн., а якщо до моменту виходу із ладу всього автомобіля які-небудь запасні частини залишаються не використаними, то кожна із них коштує всього лише 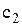 грн. Якщо усі запасні частини комплекту витрачені, то для того, щоб дістати ще один запасний блок, необхідно витратити 26000 грн.
грн. Якщо усі запасні частини комплекту витрачені, то для того, щоб дістати ще один запасний блок, необхідно витратити 26000 грн.
Параметри моделі:
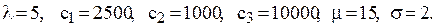
3.14. Автотранспортна фірма закуповує двигуни до імпортних автомобілів. Попит на двигуни випадковий і описується розподілом Пуассона із середнім значенням 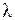 одиниць на рік. Закупівельна вартість двигуна дорівнює
одиниць на рік. Закупівельна вартість двигуна дорівнює 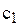 тис. доларів. Щорічний прибуток від експлуатації двигуна складає
тис. доларів. Щорічний прибуток від експлуатації двигуна складає 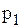 тис. доларів. Відомо, що через
тис. доларів. Відомо, що через  років зберігання вартість кожного двигуна у наслідок старіння (фізичного чи морального) знижується до
років зберігання вартість кожного двигуна у наслідок старіння (фізичного чи морального) знижується до  тис. доларів. Витрати, пов’язані із зберіганням одного двигуна протягом часу
тис. доларів. Витрати, пов’язані із зберіганням одного двигуна протягом часу 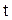 є функцією часу і дорівнюють
є функцією часу і дорівнюють  де
де  – ціна запасного двигуна, І – коефіцієнт пропорційності, який є коефіцієнтом вартості витрат на збереження запасів в одиницю часу на одиницю капіталу, вкладеного у запаси,
– ціна запасного двигуна, І – коефіцієнт пропорційності, який є коефіцієнтом вартості витрат на збереження запасів в одиницю часу на одиницю капіталу, вкладеного у запаси, 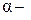 коефіцієнт пропорційності часу зберігання запасу. Втрати, пов’язані із дефіцитом двигуна є функцією часу і дорівнюють
коефіцієнт пропорційності часу зберігання запасу. Втрати, пов’язані із дефіцитом двигуна є функцією часу і дорівнюють  , де
, де 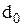 – постійна величина,
– постійна величина, 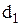 – втрати пропорційні часу наявності дефіциту. Автобус повинен пропрацювати 10 років. Двигуни можуть бути замовлені тільки одночасно із закупівлею автобусів.
– втрати пропорційні часу наявності дефіциту. Автобус повинен пропрацювати 10 років. Двигуни можуть бути замовлені тільки одночасно із закупівлею автобусів.
Визначити, скільки запасних двигунів s повинна закупити фірма, щоб очікуваний прибуток від експлуатації автобусів був максимальний.
Параметри моделі: 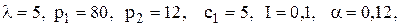

Читайте також:
- Rete-алгоритм
- Алгоритм
- Алгоритм
- Алгоритм 1.
- Алгоритм 2
- Алгоритм RLE
- Алгоритм безпосередньої заміни
- Алгоритм Берлекемпа-Мессі
- Алгоритм відшукання оптимального плану.
- Алгоритм Гоморі
- Алгоритм Дейкстри.
- Алгоритм Деккера.
| <== попередня сторінка | | | наступна сторінка ==> |
| Алгоритм реалізації моделі | | | VI. РАДІАЦІЙНИЙ, ХІМІЧНИЙ, БІОЛОГІЧНИЙ ЗАХИСТ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |