
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Методичні вказівки до практичної роботи №2
1 Тема Вибірка. Варіаційний ряд. Графічне зображення вибірки.
Числові характеристики вибірки.
2 Мета Набути навички та вміння складати варіаційний ряд, будувати полігон та гістограму відносних частот, знаходити статистичну функцію розподілу та будувати її графік, обчислювати числові характеристики вибірки.
3 Теоретичні відомості
Нехай з генеральної сукупності вилучена вибірка, і у кожного з вибраних елементів замірялась якась характеристика х (це може бути, наприклад, зріст людини або міцність деталі);нехай значення x1 спостерігалось m1 разів; x2-m2 разів,.., xk-mk разів, тоді об'єм вибірки  .
.
Значення xi, що спостерігаються, називаються варіантами, числа спостережень mi - частотами, а відношення цих чисел до об'єму вибірки 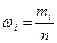 - відносними частотами.
- відносними частотами.
Послідовність варіант, записаних у зростаючому порядку з вказівкою відповідних їм частот, називається варіаційним рядом розподілу. Статистичний розподіл можна задати також у вигляді послідовності інтервалів (розрядів) і відповідних їм частот (відносних частот). Довжина інтервалу обчислюється за формулою
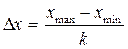 ,
,  , k-кількість інтервалів (від 5 до 20). Частота, відповідна інтервалові, дорівнює сумі частот варіант, що попали у цей інтервал. Так роблять у випадку, коли число різних варіант дуже велике.
, k-кількість інтервалів (від 5 до 20). Частота, відповідна інтервалові, дорівнює сумі частот варіант, що попали у цей інтервал. Так роблять у випадку, коли число різних варіант дуже велике.
Якщо у прямокутній системі координат Ох  зобразити точки (xi;
зобразити точки (xi; 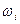 ) і сполучити сусідні точки відрізками, то одержимо ламану, що зветься полігоном відносних частот. У випадку інтервального ряду розподілу користуються гістограмою. Для її побудови на осі абсцис відкладають інтервали. На кожному з них, як на основі, будують прямокутник з висотою, рівною
) і сполучити сусідні точки відрізками, то одержимо ламану, що зветься полігоном відносних частот. У випадку інтервального ряду розподілу користуються гістограмою. Для її побудови на осі абсцис відкладають інтервали. На кожному з них, як на основі, будують прямокутник з висотою, рівною  .
.
Статистична функція розподілу 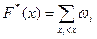 , де сума справа береться по усіх тих і, для яких хі < х.
, де сума справа береться по усіх тих і, для яких хі < х.
Числові характеристики вибірки.
1. Вибіркове середнє 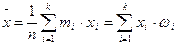
2. Вибіркова дисперсія  .
.
Виправлена вибіркова дисперсія  .
.
3. Середнє квадратичне відхилення  .
.
Виправлене середнє квадратичне відхилення 
4 Розв’язування типових прикладів
Практична робота № 1
1 Тема Вибірка. Графічне зображення вибірки. Числові характеристики вибірки
2 Мета Навчитись складати статистичний розподіл вибірки; навчитись будувати полігон та гістограму частот; складати статистичну функцію розподілу та будувати її графік; обчислювати числові характеристики вибірки.
3 Завдання Дана вибірка
547 547 549 540 560 551 552 553 557 549 545 546 545 548 550 551
552 555 558 548 569 542 560 548 550 552 551 557 558 551 552 557
546 549 553 548 549 550 558 551 549 543 548 535 537 550 556 555
550 548 543 546 554 533 552 556 549 546 568 554 552 551 558 559
554 557 558 552 558 526
3.1 Скласти статистичний розподіл вибірки.
3.2 Побудувати полігон частот.
3.3 Побудувати гістограму частот.
3.4 Скласти статистичну функцію розподілу та побудувати її графік.
3.5 Обчислити числові характеристики вибірки.
4 Виконання завдання
4.1
| Х | ||||||||||||
| mi |
| X | |||||||||||||
| mi |
Так як досить багато різних значень, то для даної вибірки складаємо інтервальний ряд. Розмах вибірки 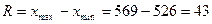 . Обираємо кількість інтервалів
. Обираємо кількість інтервалів 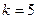 ( число
( число 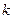 беруть в межах від 5 до 20). Довжина інтервалу
беруть в межах від 5 до 20). Довжина інтервалу 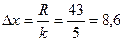
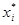
| 530,3 | 538,9 | 547,5 | 556,1 | 564,7 |

| 
| 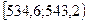
| 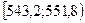
| 
| 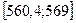
|
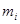
| |||||
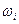
| 
| 
| 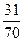
| 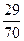
| 
|

| 0,23 | 0,7 | 3,6 | 3,37 | 0,23 |
4.2 Будуємо полігон частот по точкам з координатами ( 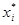 ;
; 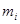 )
)

4.3 Будуємо гістограму частот: на інтервалах довжини  будуємо стовпчики висотою
будуємо стовпчики висотою 

4.4 Складаємо статистичну функцію розподілу та будуємо її графік

4.5 Обчислюємо числові характеристики вибірки
а) вибіркове середнє
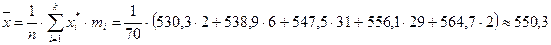
б) вибіркова дисперсія

в) вибіркове середнє квадратичне відхилення

г) виправлена вибіркова дисперсія
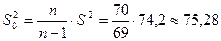
д) виправлене середнє квадратичне відхилення
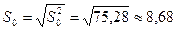
5 Висновок Навчився складати статистичний розподіл вибірки, будувати полігон та гістограму частот, складати статистичну функцію розподілу та будувати її графік, обчислювати числові характеристики вибірки.
Методичні вказівки до практичної роботи №2
1 Тема Перевірка статистичних гіпотез. Критерій Пірсона
2 Мета Навчитись перевіряти гіпотезу про нормальний закон розподілу за критерієм Пірсона
3 Теоретичні відомості
Схема міркувань при перевірці гіпотези за допомогою критерію згоди Пірсона складається з подальшого: висуваємо гіпотезу Н0: X ~ N(α;σ) випадкова величина розподілена за нормальним законом, при конкуруючій гіпотезі Н1: X ~ N(α;σ), випадкова величина не розподілена за нормальним законом.
Для перевірки гіпотези:
1) Складають інтервальний ряд.
2) Обчислюють ймовірності попадання випадкової величини X у часткові інтервали (xj-1; xj) ,для цього треба попередньо пронормувати величину, тобто знайти значення 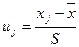 .
.
Pj = P{xj-1 < X < xj} = P{uj-1 <X <uj}= Ф(uj) –Ф(uj-1).
3) Визначають теоретичні частоти прі часткових інтервалів.
4) Обчислюють вибіркову статистику (критерій)
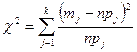
Якщо нульова гіпотеза вірна, то при n → ∞ закон розподілу даної статистики χ2, незалежно від виду функції F (х), прямує до закону розділу χ2 з числом ступенів волі r = k - f - 1 (k – кількість інтервалів; f – кількість параметрів гіпотетичної функції F (х), для нормального розподілу f=2).
5) По таблицям 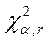 – розподілу (див. додатки), по заданому рівню значущості a і кількості степенів волі r = k - f - 1 знаходять критичне значення
– розподілу (див. додатки), по заданому рівню значущості a і кількості степенів волі r = k - f - 1 знаходять критичне значення 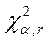 . Порівнюючи значення вибіркової статистики χ2, що спостерігається, з критичним значенням
. Порівнюючи значення вибіркової статистики χ2, що спостерігається, з критичним значенням 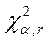 , приймають одне з двох рішень:
, приймають одне з двох рішень:
- якщо χ2 < 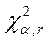 , то не існує потреби для відхилення нульової гіпотези;
, то не існує потреби для відхилення нульової гіпотези;
- якщо χ2 ≥ 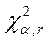 , то приймається конкуруюча гіпотеза Н1.
, то приймається конкуруюча гіпотеза Н1.
4 Розв’язування типових прикладів
Практична робота № 2
1 Тема Перевірка статистичних гіпотез за критерієм Пірсона.
2 Мета Навчитись перевіряти статистичні гіпотези за критерієм Пірсона.
3 Завдання Використовуючи критерій Пірсона при рівні значущості 0,05 перевірити, чи узгоджується гіпотеза про нормальний розподіл генеральної сукупності Х із заданим емпіричним розподілом (вибірка із практичної роботи № 1).
4 Виконання завдання
4.1
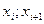
| 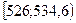
| 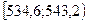
| 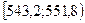
| 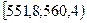
| 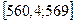
|
|
Висуваємо гіпотезу 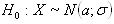 - випадкова величина розподілена за нормальним законом, при конкуруючій гіпотезі
- випадкова величина розподілена за нормальним законом, при конкуруючій гіпотезі 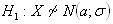 - випадкова величина не розподілена за нормальним законом.
- випадкова величина не розподілена за нормальним законом.
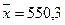
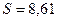
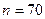
4.2 Пронормуємо випадкову величину
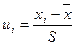
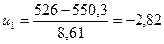
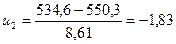
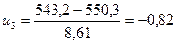
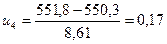
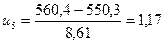

| 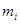
| 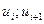
| 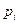
| 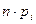
| 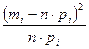
|
| 526;534,6 | 2 | -2,82;-1,83 | 0,0312 | 2,18 | 0,015 |
| 534,6;543,2 | 6 | -1,83;-0,82 | 0,1697 | 11,88 | 2,91 |
| 543,2;551,8 | 31 | -0,82;0,17 | 0,3642 | 25,49 | 1,91 |
| 551,8;560,4 | 29 | 0,17;1,17 | 0,3115 | 21,81 | 2,37 |
| 560,4;569 | 2 | 1,17;2,17 | 0,088 | 6,16 | 2,81 |
∑=10,015
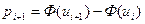
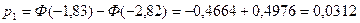
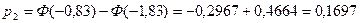
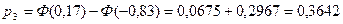
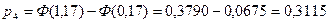
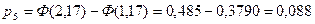
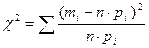
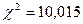
За таблицею критичних точок розподілу 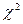 при
при 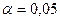 та числі ступенів волі
та числі ступенів волі 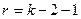 , де
, де 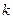 - кількість інтервалів,
- кількість інтервалів, 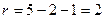 ,знаходимо
,знаходимо 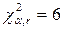 .
.
Так як 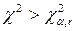 ,то гіпотеза
,то гіпотеза 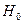 відхиляється, тобто випадкова величина не розподілена за нормальним законом.
відхиляється, тобто випадкова величина не розподілена за нормальним законом.
5 Висновок
Я навчився перевіряти статистичну гіпотезу за критерієм Пірсона.
Список літератури
1 Вища математика: спеціальні розділи: Підручник: У двох книгах.Книга 2/ Г.Л.Кулініч, Є.Ю. Таран та ін.; За ред. Г.І. Кулініча. – К.:Либідь, 1996, – 336 с.
2 Гмурман В.Е. Руководство к решению задач по теории вероятностей и
математической статистике. Учеб.пособие для втузов. – М.: Высш. шк.,2004, – 404 с.
3 Математика для техникумов. Алгебра и начала анализа: Учебник Ч.2/Каченовский М.И. и др.; Под ред. Г.Н.Яковлева. – М.:Наука.Гл.ред.физ.-мат.лит., 1988. – 272с.
4 Шкіль М.І. та ін. Алгебра і початки аналізу: Підручник для 10-11 класів серед. закладів освіти/ М.І. Шкіль, З.І. Слєпкань, О.С. Дубинчук, – К.:Зодіак-ЕКО,1998. – 608с.
Читайте також:
- I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
- II. Вимоги безпеки перед початком роботи
- II. Вимоги безпеки праці перед початком роботи
- III. Вимоги безпеки під час виконання роботи
- III. Вимоги безпеки під час виконання роботи
- Internet. - це мережа з комутацією пакетів, і її можна порівняти з організацією роботи звичайної пошти.
- IV. Вимоги безпеки під час роботи на навчально-дослідній ділянці
- S Визначення оптимального темпу роботи з урахуванням динаміки наростання втоми.
- VII. Прибирання робочих місць учнями (по завершенню роботи) і приміщення майстерні черговими.
- Аконність залишення засуджених у слідчому ізоляторі для роботи з господарського обслуговування.
- Актуальні методи соціальної роботи
- Актуальність проблеми професійної етики соціальної роботи
| <== попередня сторінка | | | наступна сторінка ==> |
| Методичні вказівки до індивідуального домашнього завдання №1 | | | WEB ПРОГРАММИРОВАНИЕ |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |