• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

ТМО розвитку просторових уявлень і уяви учнів.

4. Що ж таке уява і уявлення учнів?Вивчення досвіду роботи вчителів початкових класів свідчить, що досить часто помилки в їхній роботі обумовлюються нерозумінням суті тих завдань, які ставляться перед ними, або неправильним тлумаченням понять, які необхідно сформувати у процесі викладання математики. Саме з огляду на сказане спробуємо з’ясувати сутність понять “уява” та “уявлення”. Як відомо, під уявою розуміють психічну діяльність, яка полягає у створенні уявлень і мислених ситуацій, які ніколи в цілому не сприймалися людиною в дійсності. Уява – це змальований в думках образ чого-небудь. Отже, уява – це здатність змальовувати собі в думках відповідно до своїх знань і бажань різні життєві ситуації, людей, предмети, явища та ін., не бачені досі. У свою чергу уявлення – це розуміння, знання чогось, що базується на життєвому досвіді. Таким чином, якщо уява – це процес, то уявлення – це результат діяльності. Виходячи із такого розуміння вказаних понять, спробуємо знайти відповідь на наступне запитання.

Якій же діяльності зі створення просторової уяви слід навчити учнів та яких результатів з формування просторових уявлень повинен досягти вчитель при викладанні математики у початкових класах, зокрема при вивченні геометричного матеріалу? – аналіз вимог державного освітнього стандарту початкової школи, навчальної програми з математики та методичної літератури, вивчення досвіду роботи вчителів-новаторів дозволяють стверджувати, що одним із основних завдань вивчення геометричного матеріалу у початкових класах є розвиток просторової уяви та уявлень молодших школярів і формування уявлень про найпростіші геометричні фігури. Результатом проведеної вчителем роботи мають бути вміння учнів:

· орієнтуватися на площині та у просторі (під, над, між, вище, нижче, праворуч, ліворуч тощо);

· відшукати передбачені програмою для вивчення геометричні фігури як серед інших геометричних фігур, так і в оточуючій дійсності;

· схарактеризувати елементи найпростіших геометричних фігур;

· сприймати й аналізувати сприйняті готові геометричні образи;

· відтворити в уяві та з допомогою побудови, малювання, вирізування чи моделювання вивчені геометричні образи тощо.

Які ж методи та форми роботи сприяють виконанню завдань з формування в учнів геометричних уявлень та уяви? – відповідно до ТМО навчання та проведених методичних досліджень при формуванні просторових уявлень та уяви учнів слід використовувати:

· особистісно-орієнтований підхід до організації навчального процесу, бо сформованість просторових уявлень і уяви дітей молодшого шкільного віку надзвичайно різноманітна;

· спостереження школярів за геометричними фігурами;

· практичні роботи з вивчення властивостей фігур на їхніх моделях;

· побудову геометричних фігур;

· розв'язування задач на розпізнавання геометричних фігур, поділ їх на частини та складання фігур із заданих частин;

· операції з геометричними фігурами, при виконанні яких слід широко використовувати прийоми матеріалізації геометричних образів і співставлення та протиставлення;

· розв'язування задач геометричного змісту на виявлення властивостей геометричних фігур, на знаходження периметру та площі;

· прийом моделювання тощо.

Яка ж система вправ використовується для формування просторових уявлень та уяви учнів? – аналіз системи вправ підручників з математики для початкових класів і методичної літератури для вчителів дає підстави стверджувати, що з цією метою використовуються принаймні наступні види вправ:

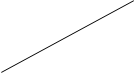
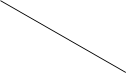
· на розпізнавання геометричних фігур, серед яких можна виділити принаймні три підгрупи: а) на розпізнавання окремої геометричної фігури; б) на відшукання вказаної геометричної фігури серед заданих; в) на розпізнавання геометричної фігури, яка є частиною іншої геометричної фігури (приклади всіх задач представлено у таблиці № 13.1.);

Таблиця № 13.1.

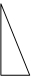
Яка це фігура?	Скільки трикутників є на малюнку?	Скільки трикутників є на малюнку?

· на моделювання геометричних фігур, серед яких можна виділити завдання на моделювання за поданим зразком чи за назвою фігури;

· на побудову геометричних фігур, серед яких виділяють принаймні наступні групи: а) на побудову за поданим зразком; б) на побудову за заданими розмірами; в) на побудову вказаної геометричної фігури;

· розв'язування текстових задач геометричного змісту, серед яких найпоширенішими є на знаходження периметра та площі.

Читайте також:

1. III.Цілі розвитку особистості
2. III.Цілі розвитку особистості
3. III.Цілі розвитку особистості
4. IІ. Актуалізація опорних знань учнів.
5. Iсторiя розвитку геодезичного приладознавства
6. V Потреби та мотиви стимулюють пізнання себе та прагнення до саморозвитку.
7. VII. ОСНОВНІ ЕТАПИ РОЗВИТКУ УКРАЇНСЬКОЇ КУЛЬТУРИ У ХХ ст.
8. VIII. Самостійна робота учнів.
9. VIII. Самостійна робота учнів.
10. VІІІ. Проблеми та перспективи розвитку машинобудування.
11. А. В. Петровський виділяє три стадії розвитку особистості в процесі соціалізації: адаптацію, індивідуалізацію і інтеграцію.
12. Агроекологічні проблеми розвитку і шляхи їх розв'язання

Переглядів: 1292