• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Трикутна підпірна стінка

Ілюстрацією рішення плоскої задачі за допомогою статечних поліномів для непрямокутної області може служити задача про трикутну підпірну стінку. Розглянемо підпірну стінку із заданим кутом 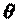у вершини, що простирається необмежено в напрямку осі 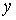(мал. 3.8). Останнє виключає вплив зв'язку стінки з основою.

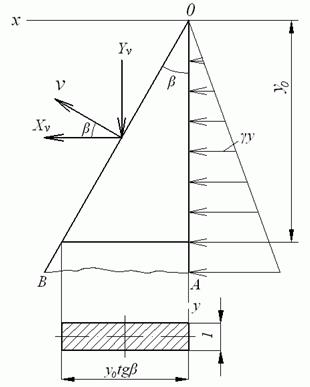
Рис.3.8. Підпірна стінка

Стінка завантажена тиском води, що змінюється за лінійним законом 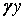( 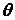— питома вага води), і власною вагою ( 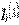— об'ємна вага матеріалу стінки). Товщина стінки в напрямку, перпендикулярному площині 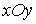, дорівнює одиниці.

Таким чином, крім поверхневого навантаження на стінку діють складові об'ємної сили

.

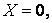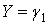(а)

Поставленим умовам можна задовольнити, взявши функцію напруг у вигляді полінома третього ступеня (3.13). З формул (3.10) з урахуванням значення складових об'ємної сили (а) одержуємо наступну систему напружень:

(б)

Для визначення вхідних сюди коефіцієнтів сформулюємо граничні умови спочатку на вертикальній грані :

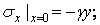
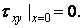
Підставляючи в ці умови напруження (б), одержуємо два рівняння:

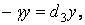
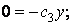
звідси

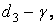
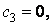
і, отже,

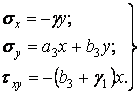
(в)

Переходимо до граничних умов на похилій грані підпірної стінки :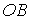

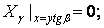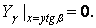
(г)

Напрямні косинуси грані:

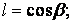
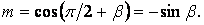
Підставляючи напруження (в) і граничні умови (г) у рівняння (3.3), одержуємо ще два рівняння для визначення коефіцієнтів:

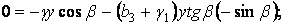
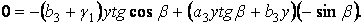
Вирішуючи їх, знаходимо:

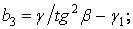
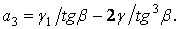
Підставляючи значення коефіцієнтів 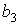і 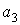, у формули (в), одержуємо складові напружень, що задовольняють всім граничним умовам і, отже, що є рішенням поставленої задачі:

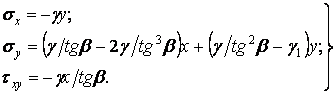
(3.27)

Дамо оцінку результатам, одержуваним при рішенні аналогічної задачі методами опору матеріалів. З погляду опору матеріалів, на підпірну стінку в перерезі 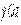діють сили (рис. 3.9): рівнодіюча гідростатичного тиску на вертикальну грань 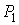яка викликає згинання, рівнодіюча власної ваги стінки 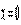, прикладена в центрі ваги трикутника і що створює позацентревий стиск.

Осі 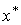й 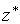— головні центральні осі перерізу 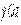. Відповідно до формул опору матеріалів,

(д)

Тут поздовжня сила

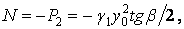
поперечна сила

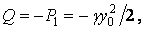
згинальний момент

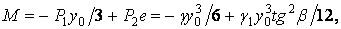
де ексцентриситет навантаження 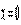щодо нейтральної осі перерізу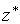

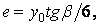
площа поперечного перерізу

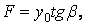
момент інерції прямокутного перерізу щодо нейтральної осі

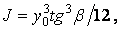
координата довільної точки 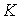щодо нейтральної осі

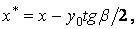
статичний момент щодо нейтральної осі частини площі перерізу, відсіченої в точці 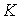прямої, паралельної цієї осі,

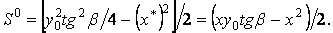
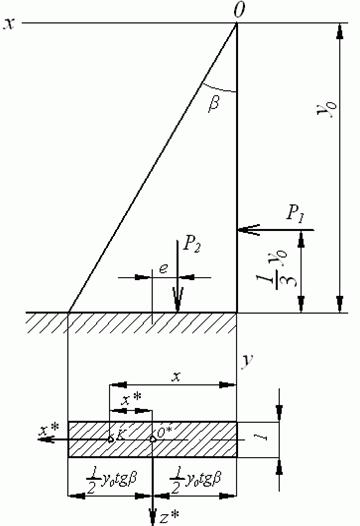
Рис. 3.9. Навантаження з погляду опору матеріалів

Після підстановки перерахованих величин у формули (д) одержуємо

(3.28)

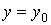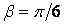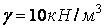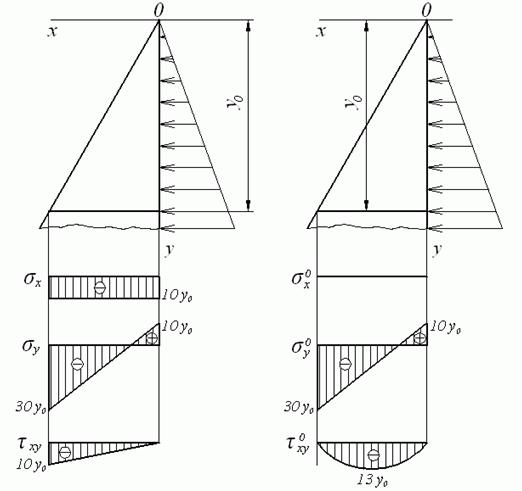
На рис. 3.10,а с показані епюри напружень на горизонтальному рівні , які підкоряються формулам (3.27), отриманим методами теорії пружності. Епюри побудовані для , і 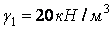. На рис. 3.10,б показані епюри тих же напружень, але отриманих методами опору матеріалів відповідно до формул (3.28).

а	б

Рис.3.10. Епюри, побудовані різними методами

Нормальні напруження 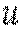, підраховані по формулах опору матеріалів, збігаються з напруженнями 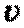, підрахованими по формулах теорії пружності. Напруженнями в опорі матеріалів зневажають через малість у порівнянні з напруженнями 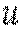, хоча, як видно з епюр, їх значення, одержуване методами теорії пружності, має той же порядок, що й напруження .

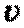Дотичні напруження, підраховані по формулах теорії пружності й опору матеріалів, відрізняються не тільки кількісно, але і якісно. Отже, рішення розглянутої задачі методами опору матеріалів не можна вважати прийнятним.

У верхової грані підпірної стінки з'являються розтягуючі напруження 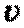, що небажано. Зі збільшенням кута 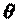ці напруження зменшуються, а потім змінюють знак. Визначимо значення 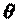, що відповідає нульовим напруженням. Вважаючи у формулі (3.27) для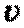

, , ,

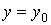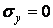одержуємо

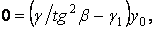
звідки

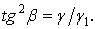
Для прийнятих раніше 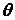і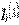

.

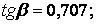
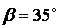Отже, щоб у похилої грані розглянутої підпірної стінки не виникали напруження, що розтягують, необхідно мати кут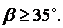

Читайте також:

1. Конструкція днищ, люків, лючків інших отворів у стінках посудин,
2. Малюнок № 7.6. Трикутна призма.
3. Порід на стінках свердловини
4. Проблеми обмеження розмірів системи. Граничні умови з фіксованими стінками.
5. Розрахунок труби з товстими стінками (задача Ламе)
6. Теплообмін випромінюванням між двома плоскими паралельними стінками при наявності екрана між ними.
7. Трикутна діаграма

Переглядів: 552