• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок балки-стінки

Балкою-стінкою називається конструктивний елемент у вигляді балки, висота якої одного порядку з довжиною перекриваємого прольоту. На прикладі розрахунку нерозрізної балки-стінки можна проілюструвати застосування до рішення плоскої задачі тригонометричних рядів. Рішення дано Б. Н. Жемочкіним.

Така балка-стінка зображена на рис. 3.11. Вона опирається на ряд колон, розташованих з однаковим кроком 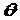, і несе навантаження, рівномірно розподілене по верхній грані. Власна вага балки-стінки при розрахунку в увагу не приймається.

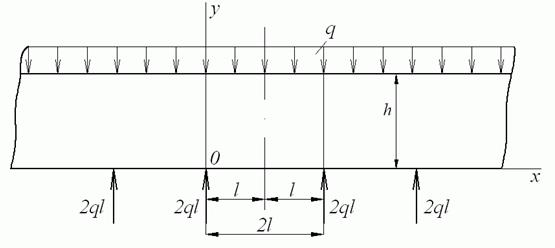
Рис. 3.11. Балка-стінка

Нехай балка-стінка має нескінченне число прольотів. Якщо виключити з розгляду крайні прольоти, то всі інші будуть перебувати в однакових умовах. У цьому випадку вісь 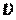, що проходить через вісь колони, є віссю симетрії. Для виконання умов симетрії функцію напружень 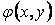варто взяти парною стосовно змінної , тобто у формулі (3.18) необхідно зберегти тільки члени, що містять :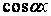

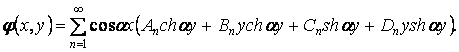
(a)

Спроби задовольнити всім граничним умовам поставленої задачі за допомогою функцій напружень (а) привели до виводу, що цієї функції недостатньо і до неї варто додати алгебраїчний поліном другого ступеня. Зберігаючи в поліномі тільки парні члени стосовно змінного , одержуємо видозмінену функцію напружень для рішення поставленої задачі:

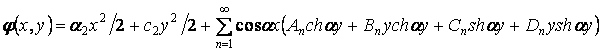
Диференціюючи цю функцію відповідно до формул (3.10) і з огляду на те, що об'ємні сили дорівнюють нулю, знаходимо складові напружень:

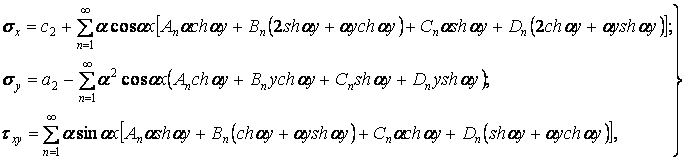
(б)

де як і раніше .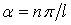

Отримані формули придатні для всіх прольотів розглянутої балки-стінки, тому що від додатка до абсциси довжини 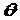функція косинуса не міняються. Отже, у відповідних точках всіх прольотів виникають однакові напруження.

Для визначення постійних, вхідних у формули (б), розглянемо граничні умови. Дві умови можна записати для верхньої грані. Тому що ця грань несе нормальне стискаюче навантаження інтенсивністю 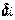, те

при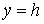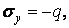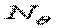

(в)

Нижня грань вільна від навантаження у всіх точках, крім тих, які лежать на осях колон. У них прикладені опорні реакції, розглянуті як зосереджені сили.

Отже, маємо ще дві умови:

при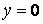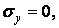

(г)

Для включення в граничні умови опорних реакцій на нижній грані розглянемо рівновагу частини балки в межах одного прольоту, відсіченою горизонтальною площиною на довільній висоті (рис. 3.12).

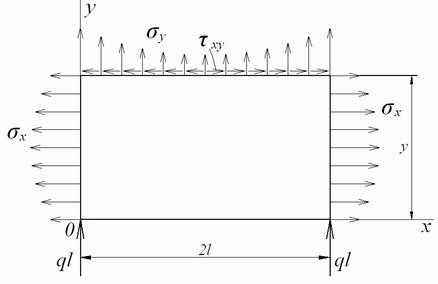
Рис. 3.12. Рівновага частини балки

Із суми проекцій на вісь всіх сил, що діють на виділену частину балки, треба п'ята умова:

(д)

Нарешті, шосту умову одержуємо з розгляду вертикальних перерізів балки. По характеру зовнішніх навантажень зусилля в них зводяться до згинального моменту і поперечної сили. Оскільки поздовжня сила відсутня, сума проекцій всіх сил на вісь дорівнює нулю:

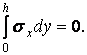
(е)

Підставляючи в умови (в)-(е) складових напружень (б), після інтегрування і приведення подібних членів одержуємо наступну систему рівнянь:

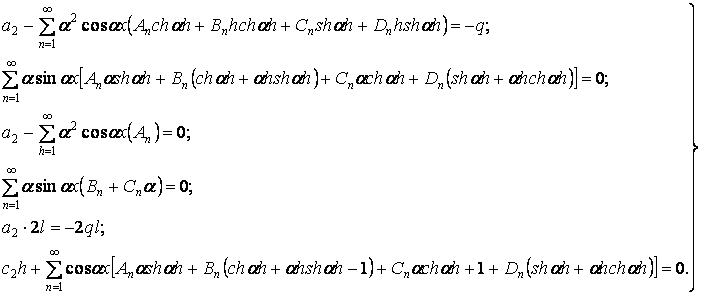
(ж)

З п'ятого рівняння (ж) знаходимо 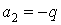. З урахуванням цього результату перше рівняння приймає вид

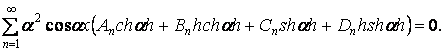
Для того, щоб суми членів ряду, не залежно друг від друга, рівнялися нулю, необхідно і досить, щоб кожний член ряду рівнявся нулю. Тому

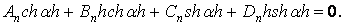
(з)

Аналогічно із другого рівняння (ж) одержуємо

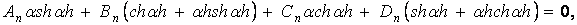
(и)

а із четвертого -

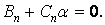
(к)

Відповідно до формул (і) і (к), вираз, що стоїть у фігурних дужках шостого рівняння (ж), дорівнює нулю і, отже,

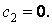
Третє з рівнянь (ж) після підстановки значення 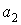приймає такий вид:

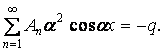
(л)

Для його рішення навантаження 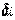розкладемо в ряд Фур'є, використовуючи відому з математики формулу

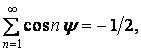
яка дійсна при 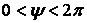. Таким чином,

.

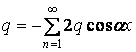Підставляємо цей ряд у формулу (л):

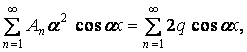
звідки знаходимо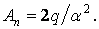

Після цього, вирішуючи спільно систему рівнянь (з)-(к), знаходимо інші постійні:

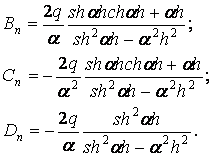
Враховуючи, що дроб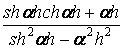і і 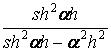для високих балок-стінок при висоті 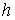, що має порядок 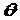, близькі до одиниці, одержуємо:

; ; .

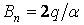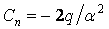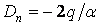Підставляючи значення знайдених постійних у формули (б), знаходимо

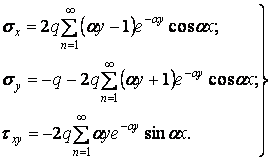
(м)

Тут гіперболічні функції замінені експонентними відповідно до залежності

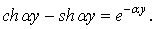
Ряди у формулах (м) сходяться дуже швидко у всіх точках, за винятком тих, які перебувають поблизу нижнього краю (при малих значеннях ).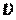

Результати обчислень для балки-стінки висотою 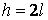наведені на рис. 3.13 у вигляді епюр нормальних напружень для двох вертикальних перерізів (на опорі і посередині прольоту) і нормальних напружень для двох горизонтальних перерезів.

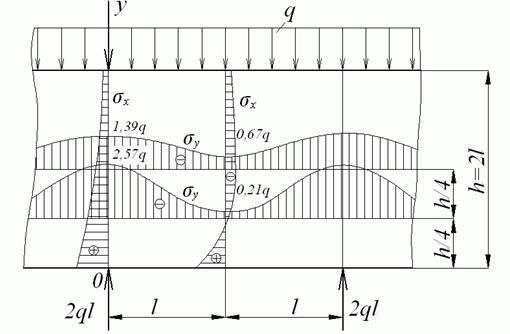
Рис. 3.13. Епюри нормальних напруг

Неважко переконатися, що ці епюри помітно відрізняються від епюр, одержуваних в опорі матеріалів.

Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. ВИБІР ДЖЕРЕЛА ФІНАНСУВАННЯ ТА РОЗРАХУНОК ВИТРАТ НА ПРАЦЕОХОРОННІ ЗАХОДИ
7. ВИБІР І РОЗРАХУНОК ОСНОВНОГО АПАРАТУ
8. Вибір та розрахунок параметрів режиму зварювання
9. Вибір устаткування для виймально-навантажувальних робіт, розрахунок його продуктивності та кількості.
10. Види норм праці, їх розрахунок
11. Вплив характеру кола на криву струму при несинусоїдній напрузі /розрахунок найпростіших кіл
12. Гідравлічний розрахунок

Переглядів: 916