• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Розрахунок труби з товстими стінками (задача Ламе)

Прикладом осесимметричної задачі є задача Ламе про товстостінну круглу трубу, що перебуває під дією внутрішніх 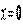і зовнішнього 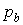рівномірних тисків (рис. 4.11).

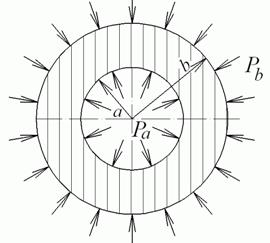
Рис. 4.11. Задача Ламе

Внутрішній радіус труби дорівнює 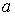, зовнішній — .

Для рішення скористаємося формулами напружень (4.35), отриманими із загального рішення осесимметричної задачі в переміщеннях. Тому що розглянута задача ставиться до випадку плоскої деформації, то зазначені формули повинні включати пружні постійні 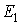й 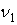. Відповідно до позначень (3.6), маємо

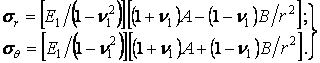
Для визначення постійних 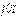і 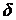маємо наступні умови на поверхні:

при ;

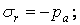
при ;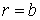

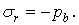
Підставляючи їх у формули (а), одержуємо:

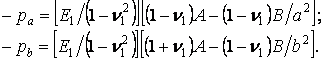
Вирішуючи спільно ці рівняння, знаходимо:

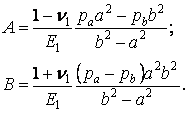
Після підстановки знайдених постійних у рівняння (а) напруги:

(4.36)

Цікаво відзначити, що сума нормальних напружень 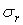і 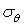у всіх точках труби однакова. Дійсно, складаючи почленно формули (4.36), знаходимо

.

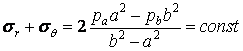(б)

У випадку плоскої деформації в поперечних перерізах труби виникають також нормальні напруження 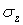. За аналогією з формулою (3.1),

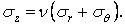
Підставляючи сюди суму напружень (б), одержуємо

.

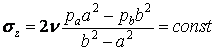Таким чином, осьові нормальні напруження 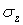постійні по довжині труби. Виключення становлять перерізи, що перебувають поблизу кінців труби, де, мабуть, труба не буде випробовувати плоскої деформації.

В окремому випадку, коли на трубу діє тільки внутрішній тиск, тобто 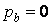, формули напружень (4.36) приймають наступний вид:

(4.37)

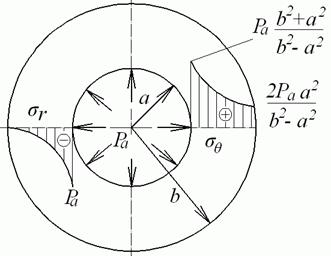
Епюри цих напружень зображені на рис. 4.12, а. Найбільші стискаючі радіальні і розтягуючі тангенціальні нормальні напруження, виникають у точках у внутрішньої поверхні труби тобто при :

;

.

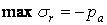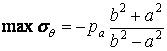У точках у зовнішньої поверхні труби (при )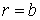

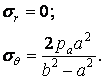
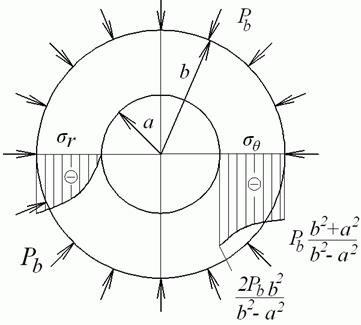
а	б

Рис. 4.12. Епюри при тільки внутрішнім або тільки зовнішньому тиску

Розглянемо трубу зовнішнім радіусом, набагато більшим внутрішнього. З формул (4.37) після розподілу чисельника і знаменника на 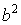одержуємо:

Переходячи до границі при 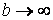, знаходимо

(в)

Це значить, що всі точки труби випробовують однакові за значенням радіальні й тангенціальні напруження, що відрізняються лише знаком. Отже, труба з нескінченно великим зовнішнім радіусом перебуває в умовах чистого зсуву. У точках внутрішньої поверхні (при ) ці напруження дорівнюють тиску 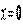, а в точках, що відповідають 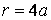, вони становлять 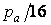. Якщо в практичних розрахунках достатня точність в 6%, то зовнішній радіус 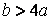можна вважати нескінченно більшим. У цьому випадку рішення не пов'язане з формою зовнішнього контуру і формули характеризують розподіл напружень для труби з будь-якою формою зовнішнього контуру за умови, що всі його точки відстоять від центра отвору на відстані, більшому ,

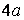В іншому окремому випадку, коли на трубу діє тільки зовнішній тиск ( 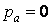), з формул (4.36) одержуємо

(4.38)

Епюри цих напружень зображені на рис. 4.12, б. У точках внутрішньої поверхні при

;

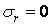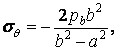
а в точках зовнішньої поверхні при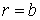

;

.

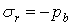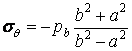Читайте також:

1. Автоматичний розрахунок суми проведення.
2. Аеродинамічний розрахунок
3. Аеродинамічний розрахунок ротора вітроустановки
4. Аналітичний розрахунок завантаження горловин
5. Аналітичний розрахунок сумарного завантаження типових перетинань
6. Бурильні труби та з’єднувальні муфти
7. Ведучі бурильні труби
8. ВИБІР ДЖЕРЕЛА ФІНАНСУВАННЯ ТА РОЗРАХУНОК ВИТРАТ НА ПРАЦЕОХОРОННІ ЗАХОДИ
9. ВИБІР І РОЗРАХУНОК ОСНОВНОГО АПАРАТУ
10. Вибір та розрахунок параметрів режиму зварювання
11. Вибір устаткування для виймально-навантажувальних робіт, розрахунок його продуктивності та кількості.
12. Види норм праці, їх розрахунок

Переглядів: 686