Проблеми обмеження розмірів системи. Граничні умови з фіксованими стінками.

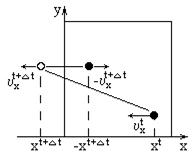
Практичну цінність при моделюванні газів, рідин, твердих тіл мають дослідження систем, що складаються з великої кількості частинок порядку 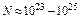. Але можливості сучасних ЕОМ не дозволяють описати таку кількість частинок, а тим більше застосувати для неї чисельний алгоритм (неможливо уявити таку швидкодіючу обчислювальну машину, яка за реальний час проведення машинного експерименту могла б зробити достатню кількість кроків в часі, щоб отримати достовірний результат, адже на кожному кроці необхідно виконати чисельний алгоритм для кожної частинки системи). Можна запропонувати провести моделювання макроскопічної системи помістивши частинки в резервуар з фіксованими стінками: якщо частинка перетинає стінку, то її нова координата визначається дзеркальною симетрією старої координати відносно стінки, а її складова швидкості, перпендикулярна до стінки, змінює лише напрям на протилежний (рис). На жаль, це не є вирішенням проблеми з двох основних причин: 1) енергія системи не залишається постійною, оскільки при відбиванні від жорсткої стінки потенціальна енергія (положення частинки) змінюється без будь-яких змін кінетичної (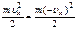); 2) частка частинок поблизу стінок в макросистемі мізерно мала, в той час як у мікросистемі (обраний резервуар) одного порядку з загальною кількістю частинок. Наприклад, якщо уявити куб (елемент кристалічної решітки), ребро якого складається з 10 маленьких кубиків (примітивних комірок), то на поверхні міститься 488 кубиків, всього в кубі - 1000, отже, майже половиною описаних кубиків потрібно знехтувати.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
Проблема розміру системи. Переваги та недоліки модельного обмеження великих систем.	\|	Періодичні граничні умови.

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.01 сек.