• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Маршрути незамкнені (ланцюги, шляхи) і замкнені (цикли, контури). Повнота. Зв’язність. Сильна зв’язність

Коли задають або шукають певну послідовність ребер (дуг), то говорять про маршрути у графах..

Означення 2.1.13. Скінченну послідовність ребер (дуг) графа 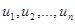(не обов’язково різних) називають маршрутом довжини п, якщо існує послідовність вершин 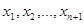(не обов’язково різних), таких що .

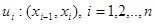Вершини 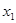і 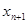називають кінцевими або термінальними.

Означення 2.1.4. Маршрут називають відкритим або незамкненим, якщо 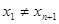і замкненим у протилежному випадку.

Означення 2.1.5. Незамкнений маршрут, у якого немає ребер (дуг), що повторюються, називають ланцюгом для неорієнтованого і шляхом для орієнтованого графа.

Означення 2.1.6. Замкнений маршрут, у якого немає ребер (дуг), що повторюються, називають циклом для неорієнтованого і контуром для орієнтованого графа.

Кажуть, що граф ациклічний або без контурний, якщо він не має циклів чи контурів.

Наприклад,

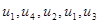– незамкнений маршрут;

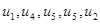– замкнений маршрут;

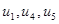– ланцюг;

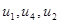– цикл.

Граф називають повним, якщо будь-які його дві вершини суміжні.

Орієнтований граф G=(Х,Г) називають повним, якщо з того, що слідує, що .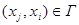

Означення 2.1.7. Неорієнтований граф G=(Х,Г) називають зв’язним, якщо в ньому існує ланцюг між кожною парою вершин.

Властивості зв’язних графів:

1) граф зв’язний тоді і тільки тоді, коли множину його вершин не можна розбити на дві непорожні підмножини 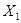та 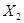так, що дві граничні точки кожного ребра були в одній і тій самій множині;

2) у зв’язному графі довільні два шляхи максимальної довжини мають спільну вершину;

3) якщо граф G=(Х,Г) – зв’язний, то граф G’=(Х,Г-u), отриманий в результаті видалення циклічного ребра и, також зв’язний.

Означення 2.1.8. Орієнтований граф називають зв’язним, якщо зв’язним є неорієнтований граф, що лежить в його основі.

Означення 2.1.9. Орієнтований граф G=(Х,Г) називають сильно зв’язним, якщо для кожної пари різних вершин 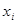і 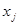існує шлях з 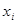до 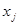і навпаки – з 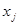до .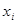

Читайте також:

1. Відкритість-замкненість, монологічність-діалогічністьу роботі практичного психолога
2. Замикання і замкнені класи булевих функцій
3. Замикання і замкнені класи булевих функцій.
4. Конфігурування маршрутизатора в командному рядку операційної системи Cisco IOS
5. Конфігурування маршрутизаторів
6. Мал. Маршрути плавань Джеймса Кука (1728–1779 рр.)
7. Мал. Маршрути плавань Х. Колумба
8. Мал. Маршрути подорожей Ібн Батути (ХІУ ст.)
9. Мал. Маршрути подорожей Марко Поло (ХІІІ ст.)
10. Маршрути вантажних автомобільних перевезень
11. Маршрутизатор (Router)

Переглядів: 1412