• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Задача про чотири фарби. Правильне розфарбування графа

В основу теорії розфарбування графа лягла задача “Про чотири фарби”. Полягала вона в тому, щоб на політико-адміністративній карті розфарбувати країни так, щоб ніякі дві країни, що мають спільний кордон, не були розфарбовані однаковою фарбою, чотирма фарбами. При цьому спільний кордон, який зображений точкою, я не лінією, не враховувався.

Ця задача зводилася до задачі про розфарбування плоского графа: маючи деяку кількість фарб, розфарбувати кожну вершину (грань) так, щоб довільні дві суміжні вершини мали різний колір.

Це одна з перших задач теорії графів. Гіпотезу про чотири фарби вперше було висунуто в 1840р. На лекціях Мьобіуса. Нею займався Де Морган (1850р.). У 1878р. Келей не зміг отримати строгого доведення цієї гіпотези. У 1890р. Хівуд довів суперечність і показав, що необхідно п’ять кольорів.

Надалі вважатимемо, що граф G – плоский, не має кратних ребер і неорієнтований.

Крім розфарбування граней графа існує його реберне і вершинне розфарбування.

Означення 2.4.1. Реберним k-розфарбуванням графа називають присвоєння ребрам графа k різних фарб.

Означення 2.5.2. Граф G(Х,Г) називають правильно реберно розфарбованим k фарбами, якщо кожне його ребро розфарбоване однією з k фарб і з того що два ребра u_i і u_j є суміжними слідує, що вони розфарбовані різними фарбами.

Означення 2.5.3. Хроматичний індекс або реберне хроматичне число Х’(G) графа G – це мінімальне число k, для якого граф має правильне реберне k-розфарбування.

Теорема Візинга. Якщо G(Х,Г) – простий граф, то або Х’(G)=D, або Х’(G)=D+1, де D - максимальний степінь вершини у графі G (для дводольного графа Х’(G)=D).

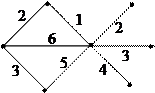
Наприклад, у заданого графа максимальний степінь вершини 6, тобто 6 ребер є суміжними і повинні бути розфарбовані різними фарбами, тому менше, ніж 6 фарб неможливо використати для правильного розфарбування. На рисунку наведено один із способів правильного реберного розфарбування заданого графа.

Означення 2.5.4. Граф G(Х,Г) називають правильно вершинно розфарбованим l фарбами, якщо кожна його вершина розфарбована однією з l фарб і якщо з (х_i,x_j)ÎГ слідує, що х_i і x_j розфарбовані різними фарбами.

Означення 2.5.5. Граф G(Х,Г) називають р-хроматичним, якщо існує правильне розфарбування вершин графа G р фарбами. Мінімальне з таких р називають хроматичним числом графа.

Читайте також:

1. Аналізуючи малюнок, зробіть висновок, яке твердження правильне.
2. Б. Задача
3. Будова осцилографа
4. Важливою ознакою класифікації є принцип побудови перетворювачів кодів, згідно з яким їх можна поділити на чотири групи.
5. Взаємне положення площин. Перша позиційна задача
6. Взаємне положення прямої і площини. Друга позиційна задача.
7. Виберіть правильне слово.
8. Визначення коефіцієнтів чотириполюсника за дослідами неробочого ходу та короткого замикання.
9. Визначення коефіцієнтів чотириполюсника за матрицею власних та взаємних опорів методу контурних струмів.
10. Вимірювання основних параметрів чотириполюсників
11. Відомі чотири основні історичні типи організації соціальної нерівності — рабство, касти, стани і класи.
12. Вправа 3. Визначте, яке з положень правильне, а яке помилкове

Переглядів: 1385