
РЕЗОЛЮЦІЯ: Громадського обговорення навчальної програми статевого виховання
ЧОМУ ФОНД ОЛЕНИ ПІНЧУК І МОЗ УКРАЇНИ ПРОПАГУЮТЬ "СЕКСУАЛЬНІ УРОКИ"
ЕКЗИСТЕНЦІЙНО-ПСИХОЛОГІЧНІ ОСНОВИ ПОРУШЕННЯ СТАТЕВОЇ ІДЕНТИЧНОСТІ ПІДЛІТКІВ
Батьківський, громадянський рух в Україні закликає МОН зупинити тотальну сексуалізацію дітей і підлітків
Відкрите звернення Міністру освіти й науки України - Гриневич Лілії Михайлівні
Представництво українського жіноцтва в ООН: низький рівень культури спілкування в соціальних мережах
Гендерна антидискримінаційна експертиза може зробити нас моральними рабами
ЛІВИЙ МАРКСИЗМ У НОВИХ ПІДРУЧНИКАХ ДЛЯ ШКОЛЯРІВ
ВІДКРИТА ЗАЯВА на підтримку позиції Ганни Турчинової та права кожної людини на свободу думки, світогляду та вираження поглядів
- Гідрологія і Гідрометрія
- Господарське право
- Економіка будівництва
- Економіка природокористування
- Економічна теорія
- Земельне право
- Історія України
- Кримінально виконавче право
- Медична радіологія
- Методи аналізу
- Міжнародне приватне право
- Міжнародний маркетинг
- Основи екології
- Предмет Політологія
- Соціальне страхування
- Технічні засоби організації дорожнього руху
- Товарознавство продовольчих товарів
Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция
Особливості множення чисел представлених у формі з плаваючою комою
Для чисел, представлених у формі з плаваючою комою, обов'язковим є представлення у вигляді мантиси і порядку (характеристики). При операції множення дії, які виконуються над мантисами і порядками, різні: мантиси перемножуються, порядки складаються. Очевидно, що результат множення може вийти ненормалізованном, тоді буде потрібно нормалізація з відповідною корекцією порядку результату. Отже, структурна схема розмножувального пристрою повинна змінитися (рис.4.3).
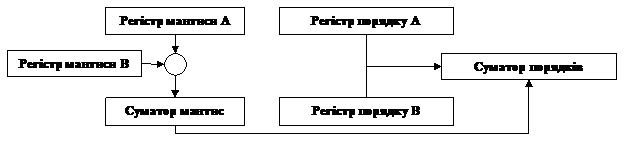
Рис. 4.3. Структурна схема пристрою множення з плаваючою комою
Розглянемо приклад виконання операцій множення чисел, заданих в прямому коді.
Приклад 4.2. Перемножити числа А = - 0,11001∙2-3 і В = 0,10011∙2 +1.
Як пристрій множення використовується схема, показана на рис. 5.3, де РгА і РгВ - відповідно регістри для порядків рА і рВ.
Розвязок: Мантиси перемножуються за правилами, розглянутим для чисел, представлених у формі з фіксованою комою. Для перемножування мантис використовується суматор прямого коду, а для складання порядків - суматор зворотного коду.
Спочатку записуються машинні зображення чисел:
[mA]пр=1.11001; [рА]об=1.100;
[mB]пр=0.10011; [рВ] об= 0.001;
Послідовність дій у процесі виконання операції множення мантис представимо в табл.4.2.
Після виконання зазначених дій знаходиться мантиса добутку [mC] пр = 1,0111011011.
Одночасно з цим над порядками проводиться операція додавання:
[pC] об = [pA] об+ [pB] об = 1,100 + 0,001 = 1,101.
Так як мантиса результату не задовольняє умові нормалізації (порушена ліва межа: 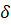 = 1,
= 1,  = 0), то виконується зсув мантиси ліворуч на один розряд: [mС] np = 1,1110110110, і корекція порядку [р'С]об = [рС]об+ 1,110 = 1,101+1,110 = 1,110.
= 0), то виконується зсув мантиси ліворуч на один розряд: [mС] np = 1,1110110110, і корекція порядку [р'С]об = [рС]об+ 1,110 = 1,101+1,110 = 1,110.
Таблиця 4.2
| Знак результату | Суматор | Регістр В | Примітка | |
Sgc = Sg1 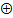 SgB=1 SgB=1 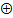 0=1 0=1
| + | РгmB: = [mB]; РгmA = [mA] РгpA = [рA]; PrpB: = [pB]; СМM: = 0;
B5=1;.СМm:= [СМm] +[ РгmA];
[ 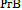 ]; [ ]; [  ];
B4=1; СМm:= [СМm] + [РгmA];
[ ];
B4=1; СМm:= [СМm] + [РгmA];
[  ]; [ ]; [ 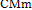 ];
b3 = 0; [ ];
b3 = 0; [  ]; [ ]; [ 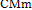 ];
b2 = 0; [ ];
b2 = 0; [  ]; [ ]; [ 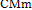 ];
b1 = 1; СМm:=[СМm]+ [РгmA];
[ ];
b1 = 1; СМm:=[СМm]+ [РгmA];
[  ]; [ ]; [ 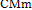 ];
Кінець ];
Кінець
| ||
| + | ||||
| + | ||||
Якщо суматор мантис містить тільки n розрядів, то після округлення виходить вихідний результат.
Відповідь: З = - 0,11110∙2-3.
При виконанні операції множення може мати місце ряд особливих випадків. Наприклад:
якщо один із співмножників дорівнює нулю, то добуток також дорівнює нулю. Отже, необхідно передбачити блокування виконання алгоритму множення і формувати результат, рівний нулю;
якщо порядок результату дорівнює найбільшій негативній величині, то необхідно формувати машинний нуль.
Ці особливі випадки можна передбачити в алгоритмі операції введенням аналізатора співмножників на нуль на початку операції (перший випадок), або корекцією добутку на підставі ознак результату (другий і третій випадки).
Читайте також:
- I. Особливості аферентних і еферентних шляхів вегетативного і соматичного відділів нервової системи
- II. Множення круглих багатоцифрових чисел на розрядні числа.
- IXX. ОСОБЛИВОСТІ ПРИЙОМУ ДО кафедри військової підготовки НАУ
- N – чисельність популяції
- VI.3.3. Особливості концепції Йоганна Гайнріха Песталоцці
- VI.3.4. Особливості концепції Йоганна Фрідриха Гербарта
- XVIII. Особливості прийому та навчання іноземців та осіб без громадянства у вищих навчальних закладах України
- А також для вегетативного розмноження.
- А. Особливості диференціації навчального процесу в школах США
- А. Особливості диференціації навчального процесу в школах США
- Агітація за і проти та деякі особливості її техніки.
- Аграрна сфера виробництва та її особливості
| <== попередня сторінка | | | наступна сторінка ==> |
| Множення чисел представлених у формі з фіксованою комою на двійковому суматорі прямого коду | | | Множення чисел, представлених у формі з фіксованою комою, на двійковому суматорі доповняльного коду |
|
Не знайшли потрібну інформацію? Скористайтесь пошуком google: |
© studopedia.com.ua При використанні або копіюванні матеріалів пряме посилання на сайт обов'язкове. |