• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тема 9. Методи мінімізації булівських функцій

9.1. Принципи спрощення ДНФ

9.2. Метод карт Карно

9.3. Метод Квайна - Мак-Класски

9.4. Евристичні методи мінімізації

9.5. Основні алгоритми евристичної мінімізації

9.1. Принципи спрощення ДНФ

Будь-якому аналітичному вираженню булевої функції відповідає логічна схема, побудована у вигляді мережі з елементів НЕ. І та АБО. Ця схема є ще однією формою завдання булевої функції.

Наприклад, логічна схема, показана на Рис. 9.1, відповідає булевої функції

Рис. 9.1. Реалізація функції на логічних елементах

У цій схемі кожному терму 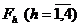функції відповідає логічний елемент І з числом входів Lh, рівному числу букв (рангу) у термі . Виходи схем І подаються на вхід елемента АБО.

Одна і та ж функція може бути представлена різними аналітичними виразами, яким відповідають різні схеми. Ці схеми можуть мати різну кількість елементів і з'єднань між ними, що визначає їх різну вартість. Для оцінки складності реалізації j-го аналітичні вирази функції fi, на практиці використовують ціну схеми по Квайну 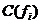. Ціна за Квайну 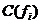дорівнює сумарному числу входів всіх елементів логічної схеми, що реалізує функцію .

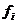Так, для схеми на рис. 3.1 маємо 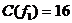. Цю оцінку можна визначити і без схеми, маючи тільки аналітичну форму представлення функції. Якщо аналітичний вираз функції має Н термів 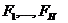і h-й терм , має 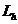літер, то отримуємо наступну оцінку:

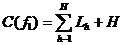(9.1)

Аналіз функції показує, що до термів може бути застосований закон склеювання, що дасть . Згідно (3.1), логічна схема для функції 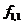повинна мати ціну по Квайну 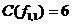З {/ \ \) = 6. Це видно і зі схеми па рис. 9.2 а.

Рис. 9.2. Реалізація, функції після застосування законів склеювання (а) і

асоціативності (б)

Застосування асоціативного закону до булевої функції 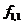призводить до виразу , що породжує схему (Рис. 9.2 б) з .

Таким чином, застосування законів булевої алгебри дозволило зменшити початкову вартість схеми в чотири рази. Очевидно, чим менша ціна за Квайну, тим менше і вартість схеми в грошовому обчисленні. Таким чином, правильне застосування законів булевої алгебри дозволяє зменшити вартість схем, якщо це можливо. Отже, одна і та ж булева функція може бути представлена різними ДНФ. Ці форми називаються еквівалентними ДНФ. Це приводить до задачі знаходження оптимальної в якомусь сенсі ДНФ серед безлічі еквівалентних ДНФ. Ця задача називається задачею мінімізації булевої функції (у класі ДНФ) і має складний комбінаторний характер.

Якщо критерієм оптимальності є мінімальне число букв (літералів) у кінцевій формулою, то мова йде про знаходження мінімальної ДНФ. Якщо мінімізується кількість кон'юнкцій у формулі, то говорять про пошук найкоротшої ДНФ. Іноді на практиці досить знайти лише так звану без надлишкову ДНФ, тобто формулу, з якої не можна видалити жодного терма (кон'юнкції) і жодного літерала.

Найпростіші методи спрощення ДНФ носять локальний характер, тобто їх застосування дозволяє спростити тільки окремі частини ДНФ. Так, при розгляді пар термів використовуються три наступні операції:

1. Поглинання, визначається формулою

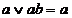(9.2)

Вираз (9.2) відображає той факт, що терм ab поглинається змінною а. Формула (9.2) доводиться наступним чином:

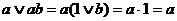
Цю формулу можна поширити на випадок довільних кон'юнкція F1 і F2:

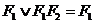(9.3)

У виразі (9.3) терми F1 і F2 можуть складатися з довільного числа змінних. Нехай, наприклад, , a 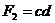, тоді з (9.3) маємо:

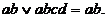
2. Склеювання, визначається формулою

(9.4)

При цьому говорять, що терми F1= ab і склеюються по булевій змінні а. Формула (9.4) доводиться наступним чином:

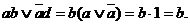
Ця формула також може бути поширена на довільні терми F1 і F2:

. (9.5)

Наприклад, нехай 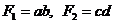, тоді

3. Видалення літерала, визначається за формулою

(9.6)

Формулу (9.6) можна довести таким чином:

Ця формула може бути розповсюджена на випадок будь-яких термів :

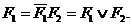(9.7)

Для попереднього прикладу маємо:

При розгляді трьох термів може застосовуватися операція узагальненого склеювання:

(9.8)

Формула (9.8) може бути доведена наступним чином:

Для спрощення ДНФ часто застосовують два наступних прийоми:

1. Дублювання термів (елементарних кон'юнкцій) функції, тобто використання закону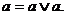

2. Диз'юнктивні розкладання термів функції з відсутньою змінною. Наприклад, терм ab може бути розкладений на змінні с, що дає . Як видно, ця операція є зворотна для операції склеювання. Можна розкласти терм ab по змінним c і d, що призведе до вираження 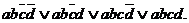Це рівносильне множенню ab на вираз

Обидва прийоми використовуються для подальшого склеювання отриманих термів з деякими з вже існуючих термів ДНФ.

9.2. Метод карт Карно

Природно, що безпосереднє застосування законів булевої алгебри для спрощення функцій є досить складним процесом. Тому на практиці використовуються методи, засновані на застосуванні карт Карно або деяких формальних методик.

Мета спрощення булевих функцій - отримання схеми з мінімальною ціною по Квайну, що відповідає аналогічному вираженню функції з мінімальним числом літер. Назвемо ДНФ з мінімальним числом літер мінімальної ДНФ (МДНФ), а процес побудови МДНФ по С ДНФ - мінімізацією булевої функції.

Розглянемо функцію , задану картою Карно на рис. 9.3.

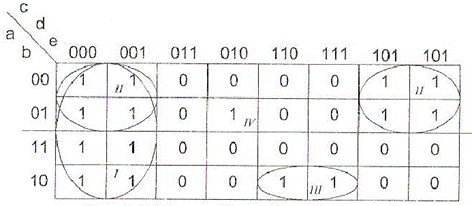
Рис. 9.3. Карта Карно для функції .

Знайдемо підфункцію Отриманий результат відповідає ребру 0010 *, що з'єднує вершини куба 00101 (терм F5) і 00100 (терм F4). Тепер знайдемо підфункцію Отриманий результат відповідає межі 0*10*, утвореною вершинами 00101 (F5), 01101 (F13), 00100 (F4) і 01100 (F12). Далі знайдемо наступну булеву підфункцію:

Отриманий результат відповідає 3-кубу, який об'єднує вершини 0, 1, 4. 5, 8, 9, 12 і 13.

З розглянутих прикладів можна зробити висновок про те, що будь-яким сусіднім клітинам довільної карти Карно відповідає n- куб, який породжує підфункцію з L-n літерами. Отримана подфункция є термом МДНФ. Назвемо n- куб булевої функції (n = 0,1 ,..., L-1) покриттям. Завдання мінімізації булевої функції зводиться до знаходження n - кубів, що покривають у сукупності усі клітини вихідної карти Карно, для яких булева функція дорівнює одиниці. Природно, що кожне з таких покриттів має включати максимальне число клітин карти Карно.

Процес мінімізації по карті Карно може бути представлений наступним чином:

1. Знайти всі пари клітин, що містять одиниці і відповідних 1-кубів. Якщо деякі клітини не можна об'єднати з іншими, то відповідні їм терми з L літерами увійдуть до мінімальну ДНФ.

2. Знайти всі четвірки, що отримуються як комбінації пар першого етапу і відповідні 2-кубів. Якщо деякі пари не можна об'єднати з іншими, то відповідні їм терми з L-1 літерами увійдуть до мінімальну ДНФ.

3. Процес продовжується до тих пір, поки на черговому етапі ніяка пара з (n-1) - кубів не об'єднується в n- куб (n = 0,1 ,..., L-1). Кожен з отриманих кубів відповідає межам, що входить до МДНФ.

Розглянемо процес мінімізації функції , зазначивши отримані покриття замкнутими лініями з римськими номерами. Результуюча МДНФ буде мати вигляд де числа в римській системі числення відповідають номерам покриттів па рис. 9.3.

З розглянутого нами методу отримання булевих функцій 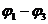випливає, що для знаходження будь-якого терма, відповідного обмеженню, необхідно виконати наступний аналіз:

1. Якщо l-я компонента наборів, що входять у межі покриття, змінюється, то відповідна їй буква не входить в результуючий терм (l= 1 ,...,L).

2. Якщо 1-а літера входить в результуючий терм, то при рівності одиниці l-я компоненти l-я літера входить в терм без інверсії.

Отже, результуючий терм Fc, який відповідає покриттю, визначається формулою

(9.9)

де 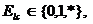0 (1) - значення l-ї компоненти для всіх наборів покриття дорівнює 0 (1), * - значення 1-ї компоненти в різних наборах покриття змінюється,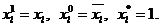

Використовуючи формулу (9.9), отримаємо такі підсумкові терми, які входять до ДНФ:

Таким чином, МДНФ функції має вигляд:

Ціна по Квайну C( )=17, а ціна по Квайну без мінімізації, згідно (9.1), дорівнює 15x5+15= 90. Таким чином, мінімізація функції зменшує ціну по Квайну більш ніж у 5 разів але порівняно зі схемою, яка реалізується по СДНФ.

Для ефективної мінімізації булевої функції по картах Карно студентам необхідно придбати деякі практичні навички, після чого мінімізація буде виконуватися автоматично.

Аналогічним чином формується і мінімальна КНФ (МКНФ). Відмінність від попереднього полягає в тому, що n- куби формуються з сусідніх клітин карти, що містять нулі. Мінімізація тепер заснована на використанні закону склеювання

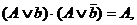
де А - довільна булева функція. У цьому випадку результуючий терм Фc визначається виразом

(9.10)

де

Розглянемо карту Карно (мал. 9.4) і знайдемо мінімальну КНФ функції . Очевидно, що в випадку КНФ ми повинні шукати область що складаються з клітинок карти, в яких записані нулі. Принцип пошуку таких покриттів не відрізняється від принципу, розглянутого раніше для ДНФ.

Рис. 9.4. Карта Карно для функції

Після знаходження покриттів I - IV очевидно, що результуюча МКНФ 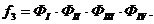Використовуючи формулу (9.10), отримаємо, що:

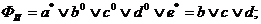
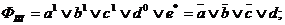
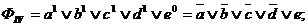
Отже, .

Розглянуті раніше функції відносяться до повністю певних функцій булевої алгебри, значення яких визначені на всіх можливих наборах змінних. Однак через фізичні особливості роботи пристрою, частина наборів можуть бути забороненими. Фізично це означає, що подібне поєднання параметрів є неможливим. Якщо функція визначена не на всіх можливих наборів вхідних змінних, то вона називається не повністю визначеною або частковою булевою функцією. Наявність заборонених наборів призводить до особливостей в отриманні МДНФ і МКНФ часткових булевих функцій.

Розглянемо деякі приклади, що ілюструють появу невизначених (заборонених) наборів.

Приклад 9.1. У приміщенні необхідно підтримувати рівень температури в межах 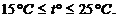Якщо , то необхідно включити обігрівач для нагрівання приміщення. Якщо 1а>) 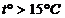, то включається кондиціонер. Необхідно поставити систему булевих функцій для управління цим процесом.

Система стабілізації температури може бути представлена наступною схемою: (рис. 9.5.)

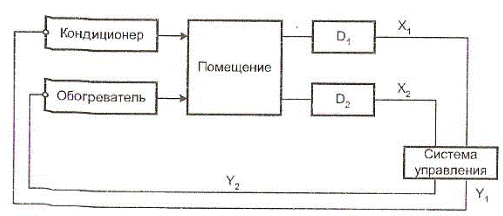
Рис. 9.5. Структурна схема системи стабілізації рівня температури

Ця система включає крім кондиціонера та обігрівача два датчики , а також систему управління. Домовимося, що х1 = 1, якщо 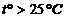, і х1 = 0, якщо ; х2 = 1, якщо і х2 = 0, якщо Система управління аналізує показання датчиків і формує два керуючих сигнали: у1 =1 - включити кондиціонер, у1 = 0-вимкнути кондиціонер, у2 = 1 - включити обігрівач, у2 = 0 - вимкнути обігрівач. Фізичний сенс сигналів відображений на рис. 9.6.

Закон функціонування системи управління задається таблицею істинності (табл. 9.1). Тут набір свідчить про ситуацію, коли температура одночасно більше 25 ° С і менше 15 ° С. Очевидно, що одночасно це неможливо і така ситуація свідчить про несправність одного з датчиків (або обох відразу). З фізичної точки зору ця ситуація неможлива, тому набір 11 є забороненим. Отже, значення функцій на цьому наборі є невизначеними, що відзначається знаком * в стовпцях .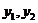

Приклад 9.2. Поставити таблицю істинності функції уз, де уз = 1, якщо і тільки якщо А 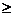В. При цьому виконується умова

Рис. 9.6. Фізичний сенс сигналів датчиків і системи управління

Таблиця 9.1

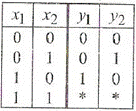
Очевидно, для представлення десяткових чисел А і В необхідно по два двійкових розряди відповідно. Нехай 00 відповідає нулю, 01 - одиниці, 10 -двійці. Тоді таблиця істинності (табл. 9.2) буде містити заборонені набори при =11 і/або =11.

Таблиця 9.2

У табл. 9.2 стовпці А і В використані в якості коментарів, а також для спрощення порівняння А і В.

На рис. 9.7 наведена карта Карло, відповідна табл. 9.2.

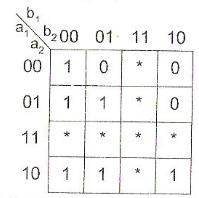
Рис. 9.7. Карта Карло функції уз

При синтезі логічної схеми знаки * повинні бути замінені нулями або одиницями. Очевидно, кожен знак * може бути замінений па 0 або 1. Таким чином, якщо функція у має n невизначених наборів, то їй відповідає повністю певних функцій. При цьому кожна заміна приводить до різної мінімальної ДНФ або КНФ.

Розглянемо ряд прикладів. Нехай всі знаки * в карті Карно (рис. 9.7) замінені нулями, що буде відповідати функції (рис. 9.8 а). З цієї карти Карно маємо МДНФ функції з ціною по Квайну C( ) = 16:

Тепер замінимо всі знаки * одиницями (рис. 9.8) і отримаємо МДНФ

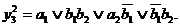
. Відзначимо, що функція включає терм , який відповідає області невизначених наборів в карті Карно (рис. 9.7).

З порівняння МДНФ і випливає, що заміна * →1 і *→ 0 повинна виконуватися так, щоб в результуючій формулою покриття включали максимально можливе число сусідніх клітин, і щоб МДНФ не містила термів, відповідних покриттям, які містять лише знаки *. Оптимальний варіант заміни наведено в карті Карно на рис. 9.8 в, звідки маємо остаточну формулу

з ціною по Квайну С ( ) = 1. Як видно з порівняння функцій - , правильна заміна * →1 і *→ 0 значно зменшує вартість схеми.

Рис. 9.8. Поліостью певні функції, відповідні часткової функції уз

При формуванні МКНФ необхідно керуватися такими самими правилами. Карта Карно (рис. 9.8г) дозволяє отримати МКНФ з ціною по Квайну

Оптимальна заміна вимагає практичних навичок, які, однак, досить швидко отримуються при відповідних тренуваннях.

Відзначимо, що при використанні формули (9.1), маємо 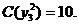Ця формула не враховує той факт, що якщо якийсь терм містить тільки одну букву, то для його реалізації не потрібен вентиль. Уточнимо формулу (9.1) і представимо її у вигляді

(9.11)

де , - булева змінна, що дорівнює одиниці, якщо і тільки якщо h-й терм ДНФ (КНФ) містить одну букву.

Тепер, згідно (9.11) для функції , наприклад, маємо наступну вартість за Квайном:

9.3. Метод Квайна - Мак-Класски

Метод Квайна - Мак-Класски є формалізованим методом мінімізації булевих функцій, що використовують практично той же алгоритм, який ми розглядали при використанні карт Карно. Проілюструємо цей метод на прикладі мінімізації функції (рис. 9.9)

Ідея методу Квайна - Мак-Класски полягає в послідовному знаходженні l-кубів по 0-кубах, 2-кубів по l- кубів і так далі. Цей процес виконується максимум за L кроків, де L - число вхідних змінних функції. На останньому етапі шукається мінімальне покриття, тобто покриття функції кубами, породжує мінімальну ДНФ.

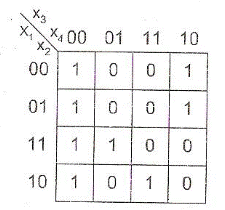
Рис. 9.9. Карта Карно функції

На першому етапі будується таблиця розмірності , де - число одиниць у карті Карно (або в таблиці істинності функції). Рядки та стовпці таблиці відзначаються кон'юнкції рангу L, відповідними 0-кубах, для яких функція дорівнює одиниці. На перетині рядка i стовпця j записується 1-куб, що покриває терми з рядка та стовпця j, якщо такий 1-куб існує. Якщо певний терм не входить ні в один з отриманих 1-кубів, то він відзначається знаком "+". що говорить про входження даного терма в мінімальну ДНФ. Назвемо цю таблицю таблиць 0-кубів. Для функції таблиця 0-кубів наведена в табл. 9.3.

Таблиця 9.3

Таблиця 0-кубів функції

З таблиці. 9.3 випливає, що терм входить в мінімальну ДНФ, а решта терми утворюють Н1 = 8 0-кубів. Оскільки таблиця 9.3 симетрична щодо її головної діагоналі в силу комутативного закону, то заповнюється тільки її права половина.

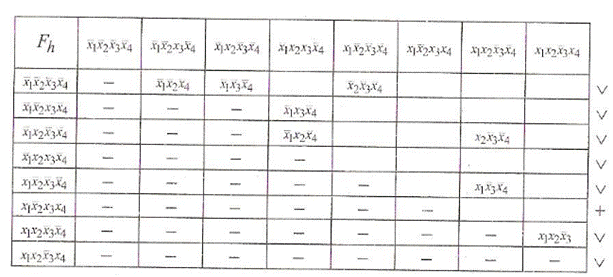
2. Будується таблиця 1-кубів розмірності 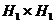, рядки і стовпці якої відзначаються однокубами, отриманими на попередньому етапі. За цією таблицею знаходяться 2-куби, для яких буде продовжуватися процес об'єднання, і 1-куби, які не склеюються з іншими l-кубами. Очевидно, однокуби, відмічені символом "+", входять в мінімальну ДНФ булевої функції. Таблиця 1-кубів функції (Табл. 9.4) має розмірність 8 x 8. З аналізу табл. 9.4 випливає, що терм входить в мінімальну ДНФ, а решта терми функції утворюють Н2 = 2 куби розмірності 2.

3. Будується таблиця 2-кубів розмірності , яка потрібна для знаходження 3-кубів, а також 2-кубів, що входять в мінімальну ДНФ. Для функції ця таблиця (табл. 9.5) має розмірність 2 x 2.

Як випливає з табл. 9.5 2-куби функції не об'єднуються, тому процес побудови кубів закінчений ( ).

Таблиця 9.4

Таблиця 1-кубів функції

Таблиця 9.5

Таблиця 2-кубів функції

4. Знаходиться покриття вихідної функції отриманими кубами, для чого може бути використаний, наприклад, метод Петрика. Цей метод заснований на побудові таблиці покриття, рядки якої відзначаються отриманими кубами, зазначеними знаком "+", а стовпці - вихідними 0-кубами. На перетині і-го рядка і j-го стовпця таблиці покриття ставиться знак 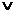, якщо вершина з стовпця j входить в куб з рядка i. Потім для кожного стовпця знаходиться диз'юнкція покриваючих його рядків, і отримані диз'юнкції для всіх стовпців логічно множаться. Застосування законів булевої алгебри дозволяє отримати ДНФ результуючої функції покриття. Кожен терм цієї ДНФ відповідає покриттю всіх стовпців таблиці покриття. З них вибирається терм, який відповідає ДНФ вихідної функції з мінімальним числом літер.

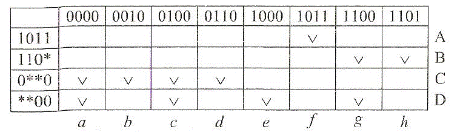
Для функції таблиця покриття (табл. 9.6) має Н = 8 стовпців (а-h) і чотири рядки (А, В, С, D).

Таблиця 9.6

Таблиця покриття функції

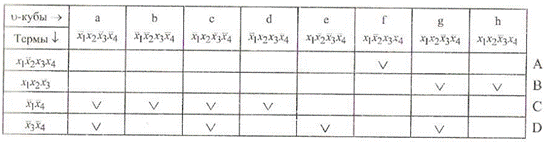
За цією таблицею будуються формули для покриття стовпців:

Далі формується формула функції покриття, що має наступний вигляд:

Таким чином, для функції існує єдиний варіант мінімальної ДНФ, а саме:

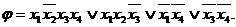
Відзначимо, що цей же варіант виходить і по карті Карно (рис. 9.9).

Вид функції 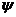можна спростити, використовуючи такі міркування. Якщо j-й стовпець має тільки одну мітку 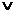, то терм з i-го рядка, де знаходиться ця мітка повинен обов'язково входити до мінімальної ДНФ. В іншому випадку 0-куб з j-го стовпця не буде відображений у мінімальної ДНФ і формула буде некоректною. Так як i-й терм обов'язково увійде до мінімальну ДНФ, то з таблиці покриття можна виключити всі стовпці, що мають позначку 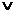на перетині з і-тим рядком. Ця процедура дозволяє зменшити кількість формул покриття стовпців і, отже, спростити функцію покриття .

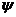Так, з табл. 9.6 виключається рядок А, так як тільки вона покриває терм f, рядок В - h (що дозволяє видалити і стовпець g), рядок С - b і d "(що дозволяє видалити і стовпці а, с), рядок D - е і g (що дозволяє видалити стовпці а, с). Таким чином, , тобто ніяких обчислень для неї не потрібно.

Якщо застосувати розглянутий метод Квайна - Мак-Класски до функції (рис. 9.10), то отримаємо терми:

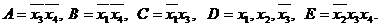
Рис. 9.10. Карта Карно функції

Побудуємо таблицю покриття для функції (табл. 9.7), в якій для спрощення замість змінних написані відповідні їм набори. Після аналізу цієї таблиці можна побачити, що терми А, С, D, Е повинні входити в остаточну функцію, що виключає з таблиці покриття стовпці а, d, g, i (покриваються А), b, c, e, f (покриваються C), i, j (покриваються D) і с, h (покриваються Е). Отже, з табл. 9.7 видаляються всі стовпці, визначаючи функцію

Як видно з цього прикладу, терм В є надлишковим і не входить в остаточний результат. Проблема пошуку надлишкових термів дуже важлива. Як показано далі, для її вирішення використовуються складні формальні методи, засновані на евристика.

Таблиця 9.7

Таблиця покриття функції

Якщо вихідна функція є частковою, то для її мінімізації використовується наступний підхід:

1. Всі невизначеності (відмічені знаком *) в карті Карпо або таблиці істинності замінюються одиницями.

2. Знаходяться терми, відповідні рядкам таблиці покриття. Терми, відповідні кубах, які включають тільки невизначені набори, виключаються з таблиці покриття.

3. Знаходиться мінімальна ДНФ вихідної функції.

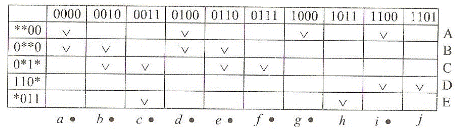
Розглянемо як приклад булеву функцію (рис. 9.11а), яка включає невизначеності.

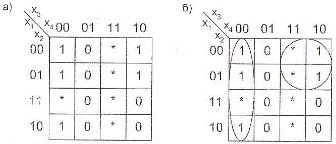
Рис. 9.11. Функція (а) і оптимальне рішення (б)

Замінивши всі знаки * одиницями, можна отримати наступні терми 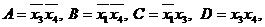чому відповідає таблиця покриття (табл. 9.8). відзначимо, що терми не входить в цю таблицю, оскільки вони покривають тільки клітини з невизначеностями. З цієї ж причини в таблицю не входять стовпці 1011 і 1111, так як вони покриваються тільки термом D.

Таблиця 9.8

Таблиця покриття функції

З аналізу табл. 9.8 випливає, що терм А повинен бути включений у ДНФ, що виключає стовпці а, d, g, h. Аналогічно, терм С також повинен бути включений в мінімальну ДНФ, що виключає стовпці b, с, е, f. Таким чином, маємо формулу що відповідає рішенню, знайденому на карті Карно (рис.9.11б).

Метод Квайна - Мак-Класски застосуємо також для формування мінімальної КНФ. У цьому випадку вихідна таблиця будується для 0-кубів, відповідних наборів, на яких функція дорівнює нулю. Щоб звести задачу до вихідної, досить в усіх таблицях замість мінтермів розглядати відповідні їм куби.

Наприклад, одержимо мінімальну КНФ функції 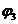(рис.9.12).

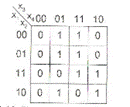
Рис. 9.12. Карта Карно функції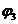

1. Побудуємо таблицю 0-кубів (Табл. 9.9).

З аналізу табл. 9.9 випливає, що терм входить в мінімальну КНФ, а решта термів утворюють Н1= 8 1-кубів.

Таблиця 9.9

Таблиця 0-кубів функції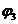

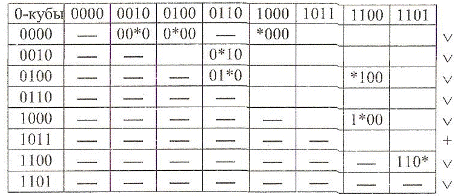
2. Побудуємо таблицю 1-кубів функції (табл. 9.10).

Таблиця 9.10

Таблиця 1-кубів функції

З таблиці. 9.10 випливає, що терм входить в мінімальну КНФ, а решта терми утворюють - 2-куби.

3. Побудуємо таблицю 2-кубів функції (табл. 9.11). З аналізу цієї таблиці випливає, що всі 2-куби входять в мінімальну КНФ і процес побудови кубів завершений. Відзначимо, що на практиці подібні таблиці можуть включати сотні і тисячі рядків. Все це ускладнює завдання мінімізації булевих функцій практичної розмірності. У зв'язку з цим на практиці використовуються кубічні подання, але тільки у вигляді рядків, які складаються з нулів і одиниць.

Таблиця 9.11

Таблиця 2-кубів функції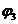

4. Побудуємо таблицю покриття функції 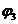(табл. 9.12).

Таблиця 9.12

Таблиця покриття функції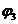

Аналіз табл. 9.12 показує, що терм А входить до МКНФ, так як тільки він включає стовпець f; терм B входить у МКНФ, так як тільки він включає стовпець h; терм С входить до МКНФ, так як тільки він включає стовпець d; терм D входить до МКНФ, так як тільки він включає стовпець e. Отже, немає потреби в побудові функції покриття, і мінімальна КНФ функції 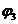має наступний вигляд:

Якщо порівнювати МДНФ і МКНФ 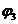, то видно, що вони утворюються однаковими кубами. При цьому у разі ДНФ куби відповідають кон'юнктивним термам, а в разі КНФ - диз'юнктивні термам. Однаковість кубів, що утворюють мінімальні форми і 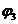, можна було очікувати, порівнявши карти Карно на рис. 9.9 і рис. 9.12. Мінімальні форми шукалися для одних і тих же 0-кубів з використанням одного і того ж методу, що і призвело до однакових результатів.

Пошук МКНФ для часткової функції проводиться аналогічно пошуку МДНФ. Природно, що при цьому враховується той факт, що необхідно аналізувати нулі функції. Метод має наступний вигляд:

1. Всі невизначеності замінюються нулями і знаходяться всі куби вищого порядку.

2. Якщо пошук кубів завершений, то куби, що покривають тільки невизначені набори, виключаються з подальшого розгляду.

Відмітимо, що на практиці часто доводиться мінімізувати системи булевих функцій, однак ці методи досить трудомісткі і виходять за рамки цієї книги.

9.4. Евристичні методи мінімізації

Розглянутий метод Квайна - Мак-Класски відноситься до точних методів мінімізації булевих функцій, що дозволяє знайти мінімальну ДНФ. Однак, як було вже зазначено, блоки ЕОМ задаються функціями, які мають десятки і сотні аргументів і тисячі термів. Такі функції, звичайно, можуть бути мінімізовані з використанням методу Квайна - Мак-Класски, однак час мінімізації буде неприйнятно великим (дні і тижні). Відзначимо, що така мінімізація може виконуватися тільки ЕОМ, а за тиждень роботи цілком може статися збій. Це означає, що процес мінімізації треба буде починати спочатку. У зв'язку з цим для вирішення практичних задач великої розмірності використовуються евристичні методи, що дозволяють знайти безнадлишкові ДНФ за прийнятний час. При цьому важливим є те, що евристичні методи не вимагають стільки пам'яті ЕОМ, як точні методи. Практичні методи використовують принцип ітераційного поліпшення рішення, крім того вони не вимагають отримання всіх первинних імплікант.

Терм називається імплікантом функції f, якщо f = 1 при = 1. Якщо імплікант не є частиною будь-якого іншого імпліканта, то він називається первинним імплікантом функції. Проблема пошуку первинних імплікантів для великої кількості аргументів дуже складна. Розглянемо карту Карно (рис. 9.13), задану деяку функцію .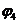

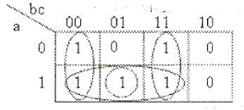
Рис. 9.11 Карта Карно для функції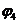

Ця карта містить чотири первинних імпліканти, відповідних обведеним областям. Це імпліканти яким відповідають куби * 00, 10 *, 1*1 і *11. При цьому карта на мал. 9.13 містить п'ять імплікант, відповідних кубів 000, 100, 101, 011 та 111. Первинний імплікант називається істотним, якщо тільки він покриває деякий мінтерм функції. Істотні імпліканти не можна видалити з кінцевої ДНФ, тому що при цьому буде синтезовано деякий інший пристрій, а не той, що було задано в початковій СДНФ. Для нашого прикладу первинний імплікант є суттєвим, так як тільки він покриває набір 000. Аналогічно, первинний импликант 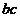є суттєвим, так як тільки він покриває набір 011. Решта імпліканти не є суттєвими.

У евристичних методах мінімізація починається з первинного покриття, яке включає всі мінтерми (набори, відповідні одиницям в карті Карно) і несуттєві набори (відмічені знаком *). Для отримання рішення використовуються чотири основних операції:

1. Розширення (Expand). При цьому кожен не первинний імплікант замінюється своїм первинним імплікантом. Потім з функції видаляються всі імпліканти, що покриваються первинними імілікантами.

2. Винятки (Reduce). Ця операція використовується для видалення з покриття надлишкових первинних імплікантів. При цьому таке видалення неможливо, якщо імплікант є істотним. Для перевірки можливості видалення імпліканта виконується перевірка, яка має показати чи є импликант істотним чи ні.

3. Переформатування (Reshape). Ця операція розглядає пари імплікантів і якщо один з імплікантів покривається іншим, то той що покриваються видаляється.

4. Безнадлишковий (Irredundant). З покриття функції видаляються несуттєві імпліканти зі збереженням покриття всіх вихідних мінттермів.

Відомий ряд практичних методів, які використовують ці операції. Так, програма PRESTO використовує тільки операцію Expand. При цьому отримують рішення швидко, але воно може бути далеким від оптимального результату. Програма MINI використовує перші три з розглянутих вище операцій. При цьому операції Reduce і Reshape використовуються для поліпшення первісного покриття, яке виходить після процедури Expand. Проте покриття може бути надмірним. Наприклад, для функції 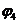може бути отримана ДНФ наступного виду: . 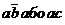Ясно, що один з термів ( ) може бути видалений. Подібні стратегії використані в програмах POP і PRESTO-L, які засновані на Методі PRESTO. Всі чотири операції використовуються у програмі ESPRESSO, яка розроблена в Каліфорнійському Університеті (США). Зараз ця програма входить практично в усі промислові пакети, що використовуються для синтезу цифрових пристроїв.

Розглянемо основні ідеї, які використовуються в методі ESPRESSO, на прикладі функції 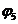(рис. 9.14).

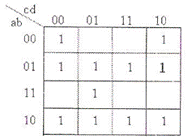
Рис. 9.14. Карта Карно функції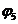

Отже, функція 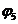має 11 минтермів, які можуть бути покриті наступними шістьма первинними імплікантами 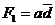(куб 0 ** 0), 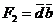(*0*0), (01 **), 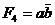(10 **), 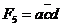(1*01), 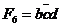(*101). При цьому імпліканти і є суттєвими. Виключивши їх із розгляду, отримаємо таблицю покриття (табл. 9.13).

Таблиця 9.13

Таблиця покриття функції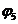

З таблиці. 9.13 можна отримати чотири мінімальних покриття, що визначається рівнянням: .

Запишемо імпліканти функції 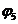в наступному порядку: 0000, 0010, 0100, 0110, 1000, 1010, 0101, 0111, 1001, 1011, 1101. Цей набір розглядається як мінімальне покриття, яке буде поліпшуватися. Застосуємо операцію Expand до імплікант в тому порядку, як вони записані. Якщо який-небудь мінтерм покривається отриманими після Expand результатом, то він відкидається. Так, імплікант 0000 може бути розширений до 0** 0, що дозволяє виключити з розгляду мінтерм 0010, 0100 і 0110. При цьому напрямок розширення, тобто, по яких розрядах мінтермів йде порівняння, задаються в програмі. Наприклад, нехай розглянуті всі імпліканти, крім 1101. Нехай при цьому отримано покриття . Залежно від напрямку розширення з 1101 можна отримати або F5 (1*01), або F6 (*101). Якщо вибір напрямку дає F5, то отримуємо покриття { }, що має 5 елементів.

Застосуємо до цього покриття операцію Reduce. Нехай вона застосовується в порядку номерів i в Fi. Первинний імплікант F1 може бути зведений до порожнього імпліканту, тому що всі його мінтерми покриті іншими імплікантами покриття а. Первинний импликант F2 може бути зведений до , тому що частина його мінтермів покривається імплікантом F4. Аналогічно, імплікант F5 може бути зведений до F5= 1101, так як частина його одиниць покривається. При цьому приходимо до покриття що має чотири елементи.

Застосувавши операцію Reshape до пари 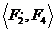, отримаємо пару кубів , де F4=10*1. Тепер маємо покриття 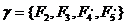. Наступне застосування операції Expand веде до покриття 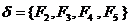, яка складається з чотирьох первинних імплікант і є мінімальним. Очевидно, що покриттю відповідає ДНФ Відмітимо, що застосування операцій Expand, Reduce і Reshape не гарантує отримання мінімального або не надлишковим покриття. Однак застосування операції Irredundant гарантує отримання не надлишковим покриття, так як вона видаляє з покриття або F1, або F2. Загалом, результат мінімізації в значній мірі визначається системою правил, які використані в евристичних алгоритмах.

9.5. Основні алгоритми евристичної мінімізації

Метою операції Expand є збільшення розміру кожного імпліканта (збільшення числа позицій, позначених знаком *) деякого покриття а. Це дозволяє видалити з покриття імпліканти меншого розміру, що покриваються отриманими первинними імплікантами.

Нехай - безліч мінтермів, для яких функція f дорівнює відповідно 0, 1 або приймає невизначений значення. Використовуємо два двійкових розряди для представлення кожної змінної: 01 для 1, 10 для 0 і 11 для *. Операція Expand виконується шляхом переходу від 1 до невизначеності *, тобто від 01 до 11. При такому переході необхідно перевірити, щоб отриманий куб покривав тільки минтерм з безлічі . Це виконується одним із двох способів:

- знаходження перетину отриманого куба з кубами з множини . Цей підхід використовується в програмах MINI і ESPRESSO;

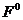- знаходження того, що новий куб покриває тільки мінтерм з множин . При цьому безліч не використовується. Такий підхід використаний в програмі PRESTO.

Результат мінімізації (як і її час) залежить від порядку вибору як розширюваних імплікант, так і позицій, в яких 1 замінюються *. У програмах MINI і ESPRESSO використовують наступний підхід для вирішення цього завдання. Кожному набору з L вхідних змінних відповідає набір, що має 2L розрядів. Формується матриця 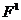і знаходяться ваги її стовпців, як суми одиниць і нулів у цих стовпцях. Потім знаходиться порозрядне створення кожного куба на вектор імплікант і результат підсумовується. Імпліканти сортуються за спаданням ваги. Природньо, що первинні імпліканти, отримані на попередніх кроках, не беруть участь в подальшій процедурі.

Приклад 9.3. Застосувати процедуру Expand до функції 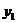(рис. 9.15)

Рис. 9.15. Карта Карно для функції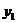

З цієї карти можна отримати три матриці кубів для множини 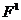, , 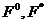які представлені на рис. 9.16. Ця матрична форма використовується для подальшої мінімізації функції.

Рис. 9.16. Матричне подання функції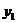

Підсумовуючи всі одиниці в колонках матриці 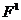, побудуємо вектор 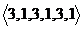. Помноживши цей вектор на перший рядок матриці 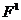, отримаємо вектор 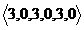, на другу - 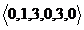, на третю - 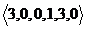, на четверту - . Підсумовуючи компоненти цих векторів, отримаємо ваги імплікант, що утворюють вектор 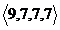. Отже, першим для Expand вибирається импликант , що має вагу 9.

Нехай 1 міняються на * зліва направо (з метою спрощення процедури). Змінивши цифру 0 в першій колонці імпликанта на 1, отримаємо вектор 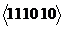, який не перетинається з векторами з матриці 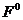. Змінивши 0 на 1 у четвертій колонці, отримаємо вектор 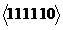, який також не пересікається з 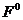. Змінивши 0 на 1 в колонці 6, одержимо вектор 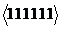який перетинається з векторами з 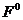. Отже отримуємо розширений імплікант 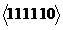, який покриває перший, другий і третій рядок матриці 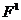, яка тепер представляється у вигляді

Тепер обробляється останній імплікант. При зміні другої колонки отримуємо вектор , який перетинається з 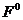. Після зміни колонки 5 отримуємо вектор , який не перетинається з 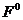. Отже маємо наступний результат, в якому остання компонента змінена з 01 на 11:

Цей результат відповідає мінімальній ДНФ 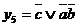, яка легко може бути отримана з рис. 9.15.

Метою операції Reduce є зменшення розмірності кожного імпліканта в початковому покритті для подальшого застосування операції Expand. Після застосування операції Reduce отримують імпліканти. Імплікант називається значущим (valid) імнлікантом, якщо він покриває вихідну функцію разом з рештою імплікантами. При цьому, операція Reduce не зменшує число імплікантів в покритті. Таким чином, покриття може залишатися надмірним. У нашому попередньому прикладі зменшення розмірності імпліканта призводить до збільшення числа імплікантів в покритті. Наприклад, якщо перетворити куб **0 в куб 0*0, то в покритті доведеться ввести куб 100. Куб 00* може бути редукований до 001 без введення додаткових кубів. Це призводить до ДНФ .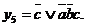

Операція Irredundant використовується для отримання покриття, яке відрізняється від вихідного максимального можливим числом віддалених надлишкових імплікант. Ця операція була вперше застосована в алгоритмі ESPRESSO і виконується після операції Expand, коли всі імпліканти в покритті є первинними. Таке покриття F ділиться на 3 класи:

- клас щодо істотних імплікантів, які покривають ті мінтерми функції, які не мають покриття іншими первинними імплікантами з F:

- клас повністю надлишкових імплікантів, до яких відносяться імпліканти, які покриваються імплікантами класу Е;

- клас 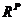частково надлишкових імплікантів , в цей клас входять імпліканти з множини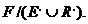

Для визначення класу необхідно перевірити, чи не покриваються імплікант 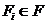імплікантами з 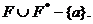Далі, для визначення елементів класу необхідно перевірити чи покриваються мінтерм 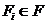імплікантами з безлічі Це дозволяє знайти безліч 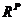як різниця між F і . Основним завданням операції Irredundant є знаходження деякої підмножини з множини 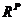, яке разом з покриває .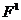

Приклад 9.4. Визначити множин , , 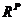функції 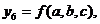заданої картою Карно (рис. 9.17).

Рис. 9.17. Карта Карно для функції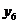

Області, обведені на карті, відповідають покриттю F, матрична форма якого наведена на рис. 9.18.

Рис. 9.18. Матрична форма покриття F функції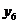

З карти Карно на рис. 9.17 можна знайти, що

.

Тепер необхідно вибрати з безлічі 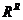мінімальну за розміром підмножину, яка разом з покриває функцію 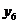. З рис. 9.17 очевидно, що це покриття . Однак для його формального пошуку необхідно застосувати досить складний алгоритм.

Процедура Essential дозволяє вибрати істотні імпліканти, що необхідно для алгоритмів точної і евристичної мінімізації. Ці імпліканти виключаються з подальшого розгляду і додаються в кінці процесу мінімізації до отриманого програмою покриття. Наприклад, перевіримо суттєвість для імпліканта 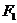(рис. 9.18). Відповідь буде позитивною, так як видалення імпліканта 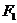залишає мінтерм 000 непокритим.

Всі ці операції використовуються в програмі ESPRESSO, яка дозволяє досить швидко знайти безнадлишкові покриття. В якості оцінки використовується процедура Cost (F), що дозволяє знайти кількість термів в покритті F. Алгоритм виконується до тих пір, поки ціна кожного чергового покриття буде менше, ніж попереднього. Якщо поліпшення не досягнуто, то робиться остання спроба поліпшення рішення, виконувана процедурою last.gasp. У цій процедурі використовуються більш складні евристичні правила, ніж для основного циклу. У зв'язку з цим час процедури last.gasp значно перевищує час ітерації в основному циклі. У спрощеній формі алгоритм ESPRESSO представлений на рис. 9.19.

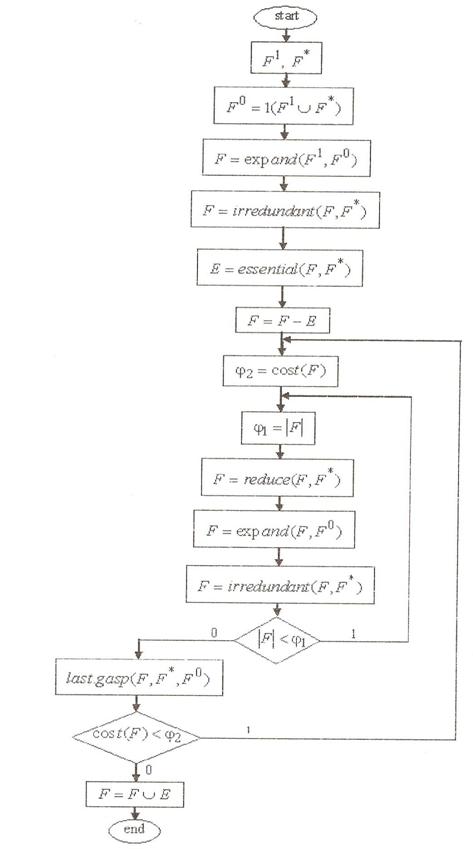
Рис. 9.19 Спрощена блок-схема алгоритму ESPRESSO

Читайте також:

1. B. Тип, структура, зміст уроку і методика його проведення.
2. Demo 11: Access Methods (методи доступу)
3. I. ЗАГАЛЬНІ МЕТОДИЧНІ ВКАЗІВКИ
4. II. МЕТОДИЧНІ ВКАЗІВКИ
5. II. УЧЕБНЫЕ И МЕТОДИЧЕСКИЕ ПОСОБИЯ, ПРАКТИКУМЫ
6. IV. КЕРІВНИЦТВО, КОНТРОЛЬ І НАДАННЯ ОРГАНІЗАЦІЙНО-МЕТОДИЧНОЇ ДОПОМОГИ ПРАКТИКАНТАМ.
7. IV. Электронное учебно-методическое обеспечение дисциплины.
8. V. ІНДИВІДУАЛЬНІ ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ ТА МЕТОДИЧНІ РЕКОМЕНДАЦІЇ ДО ЇХ ВИКОНАННЯ
9. V. Обов'язки методиста кафедри педагогіки
10. VIІ. Короткі методичні вказівки до роботи студентів на практичному занятті
11. А) Методика проведення заняття
12. А) Методика проведення заняття

Переглядів: 2720