• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Резонанс струмів. Добротність паралельного коливального контуру

Повернемося до виразу (4.21) для кола, схему якого зображено на рис. 4.33:

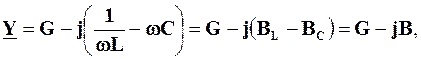
де B=B_L-B_C.

Підбираючи величини w, L та С, можна добитися того, що реактивні провідності індуктивного та ємнісного елементів дорівнюватимуть одна одній:

B_L=B_C=B₀.(4.22)

При цьому реактивна провідність кола дорівнюватиме нулю:

B=B_L-B_C=В₀-В₀=0,

а комплексна провідність буде чисто активною і дорівнюватиме величині G:

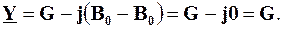
Повна провідність також дорівнюватиме величині активної провідності:

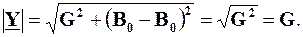
Крім того, з виразу 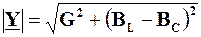випливає, що G є мінімальним значенням, яке може приймати величина повної провідності. Наприклад, якщо залишити недоторканими L та Сі змінювати лише величину w, то величина 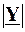змінюватиметься так, як це показано на рис. 4.34. Означивши повний опір кола 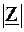виразом 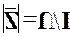та порівнявши його з наведеним вище виразом 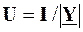, дійдемо висновку, що 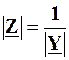. Тобто повний опір кола, схему якого зображено на рис. 4.33, є обернено пропорційним повному опору провідності цього кола, і на частоті w, на якій 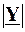сягає мінімуму, величина 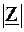сягає свого максимуму, який дорівнює .

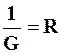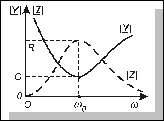
Рис. 4.34

На кутовій частоті w₀, на якій виконується рівність B_L=B_C, дорівнює нулю аргумент комплексної провідності, оскільки

.

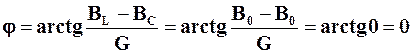У підрозділі 4.6.1 показано, що початкова фаза напруги обчислюється як j_U=j_I+j, тому при виконанні умови B_L=B_C маємо:

j_U=j_I+0=j_I,

тобто за вказаної умови струм збігається за фазою з напругою.

Режим роботи кола, утвореного паралельно з’єднаними індуктивним та ємнісним елементами (наявність резистора не є обов’язковою), при якому реактивна провідність кола дорівнює нулю, називають резонансом струмів.

Кутову частоту w₀, на якій має місце резонанс струмів, називають резонансною кутовою частотою.

Коло, схему якого зображено на рис. 4.33, називають паралельним коливальним контуром.

За означенням, при резонансі струмів на частоті w₀ маємо B_L(w₀)=B_C(w₀), тобто 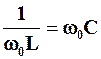. Звідси отримуємо дуже важливі формули

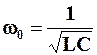(4.23)

та

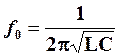. (.24)

Ці формули визначають величину резонансної частоти через параметри ідеальних конденсатора та котушки, що складають паралельний коливальний контур.

Згідно з (4.22) та (4.23) маємо (див. підрозділ 4.5.2), що 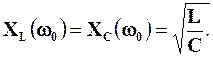Цю величину , як і для послідовного коливального контуру, позначимо як r і назвемо характеристичним опором паралельного коливального контуру.

Оскільки вхідна напруга 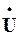прикладена як до індуктивного, так і до ємнісного елементів, то при резонансі маємо рівні діючі значення (або амплітуди) струмів у цих елементах:

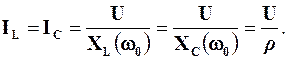
Але 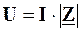. При резонансі струмів 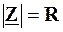, тому в цьому режимі U=I×R. Тому .

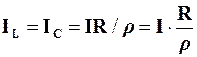Введемо добротність паралельного коливального контуру

.

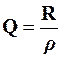Тоді при резонансі струмів діюче значенняI вхідного струму пов’язане з діючими значеннями струмів у індуктивному та ємнісному елементах, як

I_L=I_C=Q×I.

У пристроях автоматики та зв’язку величина паралельногорезистора R (див. рис. 4.33), як правило, набагато більша за r, тому в них Q>>1. Отже, при резонансі струмів величини струмів у індуктивному та у ємнісному елементах паралельного коливального контуру в Q раз більші ніж величина вхідного струму I, що й обумовило назву “резонанс струмів” для розгляданого режиму роботи цього кола.

Змінюватимемо подумки частоту вхідного струму при постійних величинах R,L,CтаI. Відмітимо, що при w=w₀ реактивні провідності індуктивного та ємнісного елементів рівні:

.

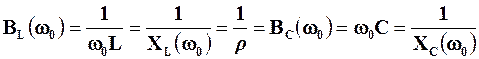Якщо w < w₀, то B_L(w) > B_L(w₀), а B_С(w) < B_С(w₀), тобто B_L(w)>B_С(w). Тому при w < w₀ маємо 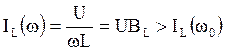, а 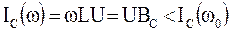, тобто 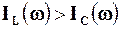. Крім того, при w < w₀ маємо також 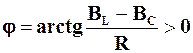, оскільки B_L > B_С. Але, як показано вище, j_U=j_I+j. Отже, при w < w₀ виконується нерівність j_U>j_I, тобто напруга на затискачах паралельного коливального контуру випереджає за фазою його вхідний струм. Кажуть, що за цієї обставини опір цього контуру носить індуктивний характер.

Векторні діаграми струмів та напруг для розгляданого випадку w < w₀ наведено на рис. 4.35[4].

Зверніть увагу на те, що в цьому випадку I_L>I. При подальшому збільшенні величини w величина 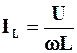зменшуватиметься, а величина I_C=wCU збільшуватиметься, аж доки при w = w₀ не настане рівність I_L(w₀)=IC(w₀).

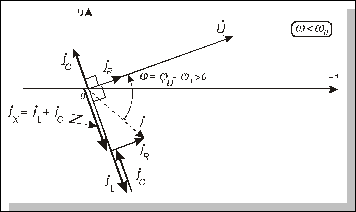
Рис. 4.35

Оскільки ж вектори та 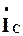спрямовані протилежно, то при w = w₀ реактивна складова струму 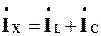дорівнюватиме нулю, а вхідний струм 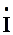дорівнюватиме струмові 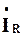. Якщо величина R буде досить великою, то 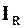буде дуже малим, а отже – таким же малим буде й вхідний струм I(w₀). Якщо R®¥, тоI(w₀)®0, в той час, як 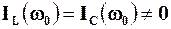. Тобто, при великих R паралельний контур споживає при w = w₀ дуже малий вхідний струм при тому, що струм в його котушці та конденсаторі зовсім не малий (як показано вище, він в Q раз більший за вхідний струм).

Для випадку w>w₀ неважко показати, що величина j буде від’ємною, тобто напруга на паралельному коливальному контурі відставатиме за фазою від його вхідного струму. Це є ознакою того, що при w>w₀ опір такого контуру має ємнісний характер.Фізичне пояснення цього полягає в тому, що при w>w₀ маємо X_L(w)>X_C(w) і більша частина вхідного струму тече шляхом найменшого опору крізь конденсатор, тобто ємнісний елемент кола.

Читайте також:

1. Аналіз паралельного інтерейсу з DSP-процесорами: запис даних в ЦАП, що під’єднаний до адресного простору пам’яті
2. Аналіз паралельного інтерфейсу з DSP-процесорами: читання даних з АЦП, що під’єднаний до адресного простору пам’яті
3. Вибірні властивості коливального контуру
4. Визначення запасів стійкості внутрішнього контуру
5. Визначення коефіцієнтів чотириполюсника за матрицею власних та взаємних опорів методу контурних струмів.
6. Для резонансних частот можливо записати
7. ДОСЛІДЖЕННЯ ПАРАЛЕЛЬНОГО КОЛА
8. Дослідження резонансних кіл
9. ДОСЛІДЖЕННЯ РЕЗОНАНСНИХ ЯВИЩ
10. ДОСЛІДЖЕННЯ РЕЗОНАНСНИХ ЯВИЩ
11. ЕЛЕКТРИЧНИЙ РЕЗОНАНС
12. ЕЛЕКТРОННИЙ ПАРАМАГНІТНИЙ РЕЗОНАНС,

Переглядів: 2258