• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Вибірні властивості коливального контуру

Резонансні фільтри, або 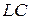-фільтри, складають з коливальних конту­рів, тобто з каскадно з’єднаних реактивних елементів різного виду. В них забезпечуються класичні умови виникнення власних коливань, а саме: перетворення енергії одного виду на інший при мінімальних необорот­них утратах енергії за період. В електричному колі — це обмін енергією між конденсатором (енергія електричного поля) і котушкою індуктивності (енергія магнітного поля).

Аналіз таких фільтрів можна вести на підставі загальної теорії коли­вальних систем, розв'язуючи диференціальні рівняння другого порядку.

Специфіка аналізу електричних коливальних систем полягає в тому, що тут маємо два види суттєво різних резонансів, властивості яких використовуються в радіоелектронних пристроях. Маються на увазі послідовний і паралельний резонанси, а також різноманітні способи утворення зв’язаних контурів. Ми поставимо за мету розглянути лише властивості окремого коливального контуру.

Вільні коливання в коливальному контурі — це майже періодичний процес обміну енергією, одноразово внесеною в контур, між електричним полем конденсатора та магнітним полем котушки. Для спрощення вважаємо спочатку, що контур ідеальний і втратами енергії в першому наближенні можна знехтувати, а максимальна енергія електричного поля дорівнює максимальній енергії магнітного поля.

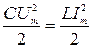. (4.25)

Обмін енергією в контурі відбувається за гармонічним законом, тобто

(4.26)

З рівняння (4.25) з урахуванням третього рівняння (4.26) знаходимо частоту власних коливань 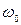і хвильовий опір 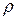контуру:

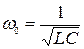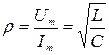; . (4.27)

У реальному коливальному контурі завжди є необоротні теплові втрати енергії, рівність (4.25) порушується і коливання з часом загасають. Це враховують уведенням у його схему (рис. 4.7, а) розподіленого еквівалентного опору 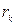. Фізичні процеси в такому контурі можна описати рівнянням другого закону Кірхгофа

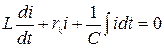(4.28)

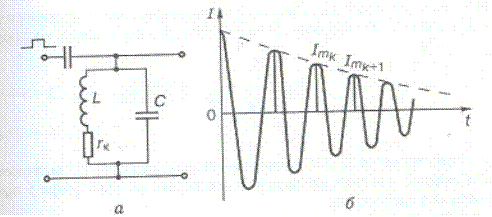
Рис. 4.7. Схема реального контуру (а) і вільні згасаючі коливання в ньому (б)

Після диференціювання (4.28) і ділення на 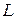дістанемо лінійне диференціальне рівняння другого порядку

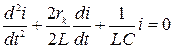, (4.29)

яке, користуючись методом підстановки, можна записати так:

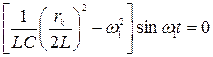. (4.30)

Оскільки остання рівність викопується при будь-яких значеннях , вираз у дужках дорівнює нулю, що можливе лише за умови

, (4.31)

де 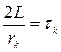— стала часу контуру.

Якщо виконується умова існування вільних коливань 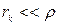, то другим членом під коренем у (4.31) можна знехтувати і розв’язок рівняння наближено записати у вигляді

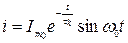, (4.32)

тобто в реальному коливальному контурі відбуваються вільні майже синусоїдні коливання струму (напруги), які загасають за експонентою (рис. 47. б). За осцилограмою можна визначити параметр, що кількісно оцінює швидкість загасання коливань. Це логарифмічний декремент загасання 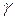, який є натуральним логарифмом відношення двох послідовних (через період То ) амплітуд напруги струму в контурі при вільних коливаннях:

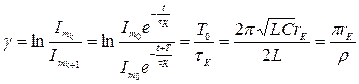. ( 4.33)

Для обчислення за (4.33) логарифмічного декременту загасання слід виміряти сусідні максимуми напруги на екрані осцилографа і прологарифмувати їх відношення.

Логарифмічний декремент загасання пов'язаний з іншим параметром коливального контуру добротністю Q — величиною, пропорційною відношенню повної енергії контуру до енергії, що втрачається в ньому за період коливань. Між добротністю та іншими параметрами контуру існує такий зв’язок:

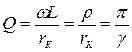. (4.34)

Збільшення втрат енергії в контурі, які відбуваються не тільки на власному розподіленому опорі 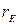, а й на опорі зовнішнього навантаження 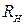, який шунтує контур, зменшує його добротність і здатність до підтримки вільних коливань. Можна довести, що за умови

або (4.35)

контур перетворюється на аперіодичну систему.

Вимушені коливання в реальному контурі створюють завдяки періодичному підведенні до нього енергії від зовнішнього джерела до компенсації необоротних втрат енергії в контурі. Якщо період зміни напруги зовнішнього джерела дорівнює періоду вільних коливань у контурі, то в ньому спостерігається резонанс. Залежно від способу з’єднання котушки і конденсатора з генератором у контурі при вимушених коливаннях може бути резонанс напруг (послідовний контур) або резонанс струмів (паралельний контур).

В обох випадках на резонансній частоті коливальний контур еквівалентний активному опору, а основною характеристикою контуру є АЧХ (резонансна крива), що визначає його вибірні можливості. Розглянемо властивості послідовного і паралельного контурів поблизу резонансної частоти.

Послідовний коливальний контур. Щоб визначити залежність коефіцієнта передачі та вхідного опору контуру від частоти, до входу чотириполюсника, зображеного на рис.4.8,а, підведемо синусоїдну напругу

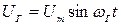. (4.36)

Коефіцієнт передачі чотириполюсника

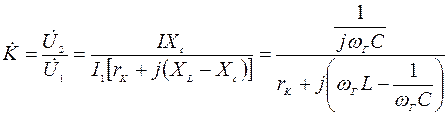, (4.37)

де 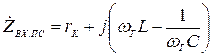— вхідний опір послідовного контуру.

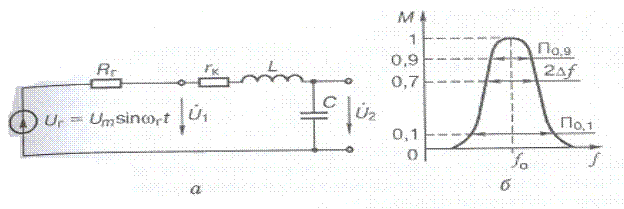
Рис. 4.8. Еквівалентна схема послідовного коливного контуру (а) і його АЧХ (б)

Розглядаючи розстроювання контуру лише поблизу резонансної частоти, тобто 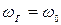, виконаємо очевидні елементарні перетворення:

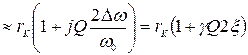, (4.38)

де 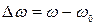— абсолютне розстроювання контуру відносно резонансної частоти; 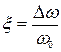—відносне розстроювання

На резонансній частоті, коли ,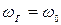

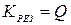; . (4.39)

Нормоване відносно коефіцієнта передачі рівняння АЧХ контуру має вигляд

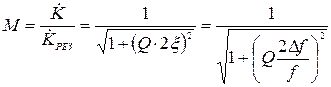. (4.40)

На АЧХ контуру (рис. 4.8, б) визначають три характерні рівні: 0,9 М. 0,7 М; 0,1 М. Ширина резонансної кривої на рівні 0,7 називається смугою пропускання контуру. Резонансна частота, смуга пропускання і добротність контуру пов’язані між собою співвідношенням

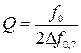. (4.41)

Важливим параметром контуру, що визначає його селективні властивості як фільтра, є коефіцієнт прямокутності АЧХ, або вибірність. Він визначається як відношення ширини резонансної кривої на рівні 0,9 до ширини цієї кривої на рівні 0,1:

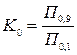. (4.42)

Послідовний коливальний контур як фільтр можна використовувати тільки з низькоомними джерелами сигналу, оскільки власний опір джерела вмикається послідовно з опором контуру і збільшує його, що призводить до зменшення еквівалентної добротності та вибірних властивостей контуру. Найчастіше послідовний коливальний контур застосовують у вхідних колах радіоприймачів як перший вибірний елемент, за допомогою якого наведена в антені напруга від сигналу радіостанції, на яку настроєно контур, може збільшуватись майже в 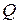разів відносно напруг сигналів від сусідніх радіостанцій.

Цей контур може відігравати роль режекторного фільтра щодо дії сильної завади на фіксованій частоті, як це показано на рис. 4.9, а. Контури 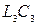і 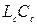настроєно на різні частоти: перший, настроєний на частоту завади , створює майже коротке замикання між точками 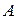та 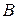; другий настроюється на частоти тих станцій, сигнали яких треба прийняти (рис. 4.9, б). Така ситуація виникає тоді, коли на рухомому об'єкті (наприклад, літаку) працюють приймач і власний передавач або коли діє постійна промислова завада.

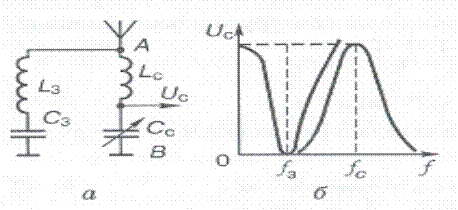
Рис. 4.9. Схема вхідного кола радіоприймача з режекторним фільтром (а) і його АЧХ (б)

При вивченні фізики в загальноосвітній школі проводять демонстраційні та лабораторні експерименти з послідовним коливальним контуром, які мають свої особливості, зумовлені технічними пара; метрами шкільного обладнання і методичними міркуваннями. Пери за все слід ураховувати, що частота власних коливань контуру не може перевищувати 10кГц. Домогтися цього можна збільшенням індуктивності 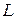, а не ємності . В іншому випадку буде дуже малим хвильовий опір контуру і коливання в ньому не виникатимуть. Для здобуття резонансу треба встановити власний опір шкільного генератора найменшим, а вольтметр для вимірювання напруги брати з найбільшим опором або використовувати міліамперметр і вимірювати резонансний струм.

Паралельний коливальний контур. Його еквівалентну схему при живленні від

Рис. 4.10. Еквівалентна схема паралельного коливного контуру при живленні від низькоомного генератора гармонічного сигналу

низькоомного генератора гармонічного сигналу зображено на рис. 4.10. Коефіцієнт передачі самого контуру дорівнює одиниці, але якщо розглядати чотириполюсник відносно входу 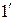, тобто включити до нього ще й внутрішній опір генератора 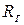, то відносно ідеального генератора коефіцієнт передачі чотириполюсника

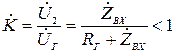. (4.43)

У будь-якому випадку 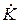тим більше відрізняється від одиниці, чим більшою є нерівність 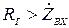. Значення 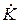в цьому разі залежить від час­тоти і сягає максимуму при резонансі, тому що значення одного з опорів подільника залежить від частоти.

Розглянемо властивості вхідного опору паралельного контуру

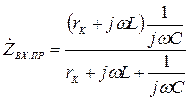. (4.44)

При будь-якій частоті поблизу резонансної вираз у чисельнику 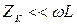, а вираз у знаменнику має вигляд (4.38). Тому вираз (4.44) перепишемо у вигляді

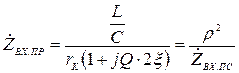. (4.45)

При резонансі

. (4.46)

Якщо послідовний контур на резонансній частоті мав мінімальний опір, то опір паралельного контуру при резонансі максимально можливий. Залежність вхідного опору паралельного контуру від частоти визначається виразом, записаним у знаменнику (4.44).

Усі сформульовані вище висновки відносно рівняння нормованої АЧХ смуги пропускання і резонансної частоти справедливі також для паралельного контуру. Проте, на відміну від послідовного, паралельний контур зберігає всі свої властивості лише при великих значеннях 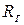, тобто його можна застосовувати тільки з високоомними джерелами сигналу Оскільки власний опір еквівалентного ідеального генератора дорівнює нулю, можна вважати, що опір 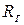приєднано паралельно контуру й еквівалентний опір такого з’єднання

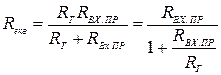, (4.47)

тобто контур ніби шунтується опором .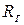

У реальних умовах кожен контур розташовується між джерелом і споживачем сигналу (навантаженням), який можна замінити опором 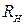. Отже, еквівалентний опір паралельного з’єднання трьох опорів

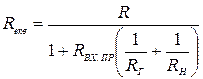. (4.48)

Відповідно еквівалентна добротність шунтованого контуру

. (4.49)

Таким чином, у реальних умовах через вплив опорів 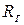та 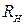еквівалентна добротність паралельного коливального контуру зменшується відносно його власної добротності, що призводить до зниження його вибірних властивостей. Особливо це слід ураховувати при використанні паралельного контуру в колах з біполярними транзисторами.

Одним з ефективних засобів зменшення впливу опорів 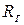й 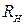на еквівалентні параметри паралельного контуру є неповне вмикання навантаження та генератора в контур, тобто приєднання лише частини одного з його елементів. Найчастіше таким елементом є котушка і тоді неповне її вмикання можна розглядати як автотрансформаторний зв'язок контуру3 генератором та навантаженням (рис. 4.11).

З теорії трансформаторів відомо, що при коефіцієнті трансформації 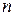відбувається не тільки зміна напруги і струму в 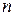разів, а й зміна еквівалентного опору в 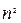разів, тобто опор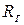и й 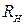замінюються еквівалентний опорами

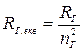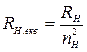; , (4.50)

де ; 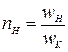— коефіцієнти вмикання з боку джерела сигналу та навантаження.

Оскільки 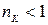, , 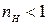значення еквівалентних опорів значно більші, ніж опорів, приєднаних до контуру. Внаслідок цього зменшується шунтувальна дія опорів схеми на контур, а його еквівалентна добротність збільшується. Безумовно, за такий здобуток доводиться позбавитися частиною коефіцієнта передачі контуру, але це легко компенсувати збільшенням підсилення сигналу в наступних колах. Головна ж властивість коливального контуру — вибірність — при цьому зберігається.

Зважаючи на властивості паралельного коливального контуру його застосовують у резонансних підсилювачах, генераторах гармонічних сигналів, модуляторах, перетворювачах частоти сигналів як їхнє власне навантаження, а також для побудови різноманітних смугових фільтрів. Оскільки вибірні властивості окремих коливальних контурів не завжди задовольняють практичні потреби, використовують системи зв'язаних контурів.

Рис. 4.11. Схема неповного вмикання котушки в паралельний коливальний контур

Читайте також:

1. А) Товар і його властивості.
2. Аеродинамічні властивості колісної машини
3. Аналізатори людини та їхні властивості.
4. Аналізатори людини та їхні властивості.
5. Атрибутивні ознаки і властивості культури
6. Багатоконтурні частотно-вибірні системи
7. Білки, властивості, роль в життєдіяльності організмів.
8. Біосфера Землі, її характерні властивості
9. Будова атомів та хімічний зв’язок між атомами визначають будову сполук, а отже і їх фізичні та хімічні властивості.
10. Будова і властивості аналізаторів
11. Будова, склад та фізичні властивості Землі
12. Векторний добуток і його властивості.

Переглядів: 5890