• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

Типи електричних фільтрів

Однією з поширених операцій, що виконуються в радіоелектронних колах, є виділення певного сигналу або частини його спектра з сукуп­ності інших сигналів та завад. Для цього використовують електричні фільтри. Виділення електричних сигналів можна здійснювати за одним з їхніх параметрів: частотою, амплітудою або тривалістю. Відповідно фільтри можуть бути частотними, амплітудними або часовими. Амплітудні та часові електричні фільтри застосовуються для виділення імпульсних і цифрових сигналів.

Частотним електричним фільтром називають вибірний чотириполюсник, що передає сигнал з найменшим ослабленням у заданій частині спектра частот, яка називається смугою пропускання (прозорості), й максимальним ослабленням за межами цієї смуги. Частота, що розділяє сму­гу прозорості та непрозорості фільтра, називається його граничною частотою, або частотою зрізу.

Класифікувати електричні фільтри можна за різними ознаками:

• за призначенням та типом частотної характеристики;

• за фізичними процесами в них;

• за наявністю або відсутністю в схемі фільтра активних елементів;

• за схемами побудови тощо.

За призначенням і типом частотної характеристики електричні фільтри поділяють на фільтри нижніх частот (ФНЧ), фільтри верхніх частот (ФВЧ), смугові, режекторні (рис.4.1).

Фільтр нижніх частот — це частотний електричний фільтр, що має смугу пропускання, розташовану нижче деякої заданої частоти зрізу, яка називається верхньою граничною частотою f_в.

Фільтр верхніх частот — це частотний електричний фільтр, що має смугу пропускання, розташовану вище деякої заданої частоти зрізу, яка називається нижньою граничною частотою f_н.

Рис. 4.2. Триланкові ланцюжкові електричні Рис. 4.3. Мостові схеми електричних

фільтри верхніх (а) і нижніх (б) частот фільтрів: а – міст Віна; б – подвійний

Т–міст

Смуговий фільтр має смугу пропускання, розташовану між верхньою та нижньою граничними частотами: .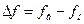

Режекторний фільтр характеризується не смугою пропускання, а смугою затримки, розташованою між двома заданими смугами пропускання.

За фізичними процесами фільтри поділяють на електричні й електромеханічні. В електричних фільтрах використовуються дискретні L-, С-, R-елементи або їхні мікросхемні аналоги. В електромеханічних фільтрах відбувається перетворення електричних коливань на механічні, фільтра­ція яких і здійснюється, з наступним оберненим перетворенням механіч­них коливань на електричні.

Частотні електричні фільтри, до складу яких входять транзистори або мікросхеми, називають активними, а решту фільтрів — пасивними.

За схемами побудови розрізняють резонаторні, ланцюжкові, мостові та цифрові електричні фільтри. Прикладами резонаторних (реактивних) фільтрів є одиничні та зв'язані коливальні контури, п'єзоелектричні, квар­цові фільтри, а також фільтри на поверхневих акустичних хвилях.

Ланцюжкові та мостові схеми фільтрів (рис.4.2 і 4.3) утворюють каскадним з'єднанням найпростіших і Г-подібних елементів, які можуть містити як L-, С-, R-елементи, так і RL- та RС-елементи. Останні з них, пока­зані на рис. 4.4, а і 4.5, а, мають перевагу перед елементами з індуктивністю, оскільки намотувальні елементи (котушки, дроселі тощо) є громі­здкими,

Рис. 4.4. Схема (а), амплітудно-частотна (б), фазочастотна (в) і перехідні (г)

характеристики елементарного ФВЧ – диференціювального ланцюжка

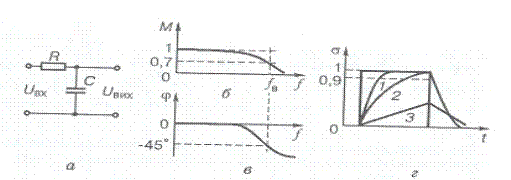
Рис. 4.5. Схема (а), амплітудно-частотна (б), фазочастотна (в) і перехідні (г)

характеристики елементарного ФНЧ інтегрувального ланцюжка

Безумовно, у розглянутій класифікації один і той самий фільтр електричних сигналів за різними ознаками належить одночасно до різних класів. Наприклад, коливальний контур, що вивчається в курсі фізики середньої школи, є смуговим резонаторним пасивним електричним фільтром із зосередженими елементами, а той самий коливальний контур для діапазону дециметрових або сантиметрових хвиль, побудований на відрізках довгих ліній, є фільтром із розосередженими елементами, хоча решта його ознак залишаються без змін.

У курсі фізики середньої школи розглядають лише найпростіші RС-фільтри (у схемах амплітудного детектора, підсилювача напруги тощо) та резонансний LС-фільтр (у схемі автогенератора, амплітудного модулятора, радіоприймача). Тому докладно зупинимося лише на цих фільтрах.

4.2. Властивості найпростіших RС-елементів

Для виділення сигналів у найпростіших RС-фільтрах використовується залежність реактивного опору конденсатора, а разом із ним і коефіцієнта передачі чотириполюсника, від частоти. Для поліпшення вибірних властивостей окремі RС-елементи з'єднують у ланцюжкові та мостові схеми.

Властивості фільтрувального елемента залежать від опору та ємності, а також розміщення радіодеталей відносно напрямку передачі сигналу. Оскільки до складу фільтра входять лише реактивні елементи одного типу (в розглядуваному випадку — ємність), при одноразовому підведенні елек­тричної енергії в колі відбувається необернений аперіодичний процес роз­рядження конденсатора через резистор із перетворенням енергії електрич­ного поля на теплоту. Тому такі фільтри іноді називають аперіодичними.

Добуток значень опору та ємності має розмірність часу і називається постійною часу елементарного фільтра

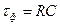. (4.1)

Вибором постійної часу і способу з'єднання елементів можна надати періодичному електричному фільтру інтегрувальних або диференціювальних властивостей, які розглядаються нижче.

Схему елементарного ФВЧ — диференціювального ланцюжка та його типові характеристики показано на рис.4.4. Послідовне вмикання конден­сатора відносно напрямку передачі сигналу приводить до того, що фільтр не пропускає постійну складову сигналу. Із збільшенням частоти опір кон­денсатора зменшується і вище деякої граничної частоти цим опором можна знехтувати. Коефіцієнт передачі фільтра

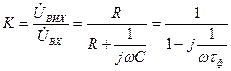. (4.2)

Рівняння амплітудно- та фазочастотної характеристик мають вигляд

(4.3)

Для рівня частотних спотворень М_н = 0,7 нижня гранична частота

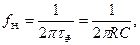(4.4)

вище якої фільтр прозорий.

У радіоелектронних колах розглянута схема найчастіше застосовується як перехідний міжкаскадний елемент, в якому конденсатор розділяє постій­ну складову струму живлення і змінну складову сигналу. Крім того, вона може використовуватись як елемент фазообертальних ланцюжків та ліній затримки сигналів, а також застосовуватись для аналогового диференцію­вання електричних сигналів, про що йтиметься нижче.

Схему елементарного ФНЧ — інтегрувального ланцюжка та його типо­ві характеристики показані на рис. 4.5. Паралельне вмикання конденсатора відносно напрямку передачі сигналу приводить до того, що із зростан­ням частоти опір конденсатора спадає і він шунтує вихід фільтра. Отже, вище деякої граничної частоти коефіцієнт передачі сигналу швидко зменшується, тобто фільтр прозорий від нульової до деякої верхньої граничної частоти. Коефіцієнт передачі фільтра

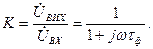(4.5)

Рівняння амплітудно- та фазочастотної характеристик мають вигляд

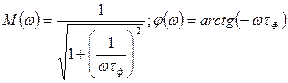(4.6)

Для рівня частотних спотворень М_в = 0,7 верхня гранична частота

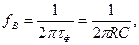(4.7)

нижче якої фільтр прозорий.

У радіоелектронних колах розглянута схема найчастіше використову­ється як детектор модульованих сигналів. Саме такою вона розглядається в курсі фізики загальноосвітньої школи. Ця схема часто застосовується в емітерних і витокових колах для усунення змінної складової напруги з метою стабілізації положення РТ транзистора та її автоматичного зміщення, а також у випрямлячах змінного струму і стабілізаторах напруги. Крім того, вона використовується для аналогового інтегрування електричних сигналів, про що йтиметься нижче.

Характеристики найпростіших фільтрувальних елементів мають дуже пологі схили відносно граничних частот, тобто їхні фільтрувальні власти­вості невисокі. Тому на практиці застосовуються складніші фільтри, що містять RС-елементи як складові. Розглянемо їх докладно.

Схеми ланцюжкових електричних фільтрів верхніх і нижніх частот, зображені на рис.4.2, складаються з трьох ланок (їх може бути і більше). Такі фільтри використовують у лініях затримки сигналу й у колах повороту фази RС-генераторів, де ці фільтри з'єднують покаскадно. Всі ланки мають однакову сталу часу. Опори резисторів можна вибирати однаковими або такими, що змінюються за законом геометричної прогресії. В табл. 4.1 наведено деякі розрахункові співвідношення стосовно розглядуваних фільтрів для частоти повороту фази на 180°.

Таблиця 4.1

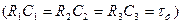
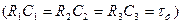
Схема на рис. 4.2, а	Кн		Схема на рис. 4.2, б	Кв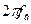

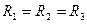
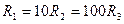
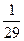
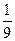
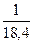
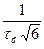
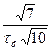
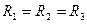
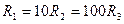
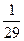
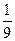
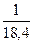
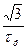
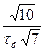
Схеми найпоширеніших мостових електричних фільтрів, які є поєднанням фільтрів верхніх та нижніх частот, показано на рис. 4.3. Якщо елементарні фільтри нижніх і верхніх частот з'єднують послідовно дістають схему фільтра, що має назву моста Віна (рис.4.3, а). Якщо для обох фільтрувальних елементів цієї схеми сталу часу вибрати однаковою, то

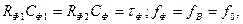(4.8)

тобто існує квазірезонансна частота 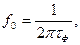на якій коефіцієнт передачі фільтра має максимум. Такий фільтр набуває властивості смугового і називається квазірезонансним.

Для підвищення вибірних властивостей мостовий фільтр можна по­будувати за схемою паралельного з'єднання чотириполюсників. Прикладом такого фільтра, ввімкненого відносно сигналу як загороджувальний, є 2Т-подібний міст. Його коефіцієнт передачі на квазірезонансній частоті

(4.9)

дорівнює нулю.

При виборі елементів такого фільтра задовольняють одну з трьох умов:

1) нульового балансу

(4.10)

2) симетрії моста

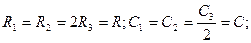(4.11)

3) найбільшої добротності моста

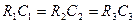(4.12)

де величини R₁, і С₂ – малі, а величини R₂ та С₁, – великі.

Найчастіше задовольняють другу умову.

У практичних схемах досить часто два резистори вмикають для поділу напруги (рис.4.6), де резистор R2 завжди шунтується ємностями монтажу, вхідними та іншими ємностями. Внаслідок цього складові спектрів, що мають різні частоти, послаблюються по-різному. Для того щоб уникнути спотворень сигналу і зробити АЧХ горизонтальною в усьому діапазоні частот, паралельно резистору умикають конденсатор 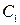, ємність яко­го

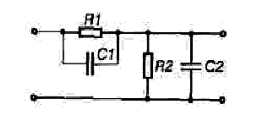
Рис. 4.6. Схема подільника напруги з частотно-незалежним коефіцієнтом передачі

вибирають, виходячи з умови

. (4.13)

У цьому разі коефіцієнт передачі подільника не залежить від частоти і визначається виразом

. (4.14)

Диференціювання сигналів можна виконувати за допомогою ФВЧ, якщо вибір його елементів задовольняє додаткові умови, які забезпечують рівність

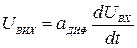, (4.15)

де 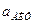—коефіцієнт пропорційності.

Ураховуючи те, що , а

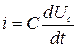(4.16)

дістаємо

. (4.17)

Оскільки похідна гармонічної функції є також гармонічною функцією, диференціюють прямокутні імпульсні сигнали й одержують ПХ схеми. Якщо тривалість імпульсу задовольняє умову , то

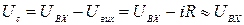. (4.18)

Таким чином,

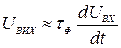, (4.19)

де .

У розглянутому випадку диференціюється незмінна на проміжку часу функція 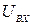(вершина імпульсу). Похідна сталої величини дорівнює нулю, тобто умовою ідеального диференціювання буде 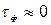. На ПХ диференціювального ланцюжка (див. рис. 4.4, г) лінія 3 відповідає умові реального диференціювання, лінія 1 — звичайному перехідному процесові за умови (4.4), а лінія 2 — умові .

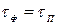Інтегрування сигналів можна виконувати за допомогою ФНЧ (див. рис 4.5, а), якщо вибір його елементів задовольняє додаткову умову, яка забезпечує рівність

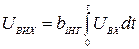. (4.20)

З причин, наведених вище, зручно розглядати інтегрування прямокутного імпульсу, тобто постійної на проміжку часу напруги. Тоді напруга на виході інтегрувального ланцюжка

. (4.21)

Ураховуючи (4.16), маємо 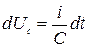, так що

. (4.22)

Якщо тривалість прямокутного імпульсу задовольняє умову , то

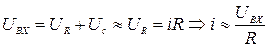. (4.23)

Тоді

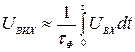, (4.24)

де .

На ПХ інтегрувального ланцюжка (див. рис. 4.5, г) лінія 3 відповідає Умові ідеального інтегрування, лінія 1 — звичайному перехідному проце­сові за умови (4.7), а лінія 2 — умові .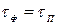

Інтегрування імпульсів застосовують в імпульсних пристроях для формування лінійно-змінної напруги, а диференціювання — для скорочення тривалості імпульсів запуску.

Читайте також:

1. Будова фільтрів
2. Види діелектричних втрат
3. Види електричних травм
4. Види електричних травм та дії електричного струму на людину.
5. Види електричних травм.
6. Види електричних травм.
7. Види електричних уражень.
8. Визначення зони розсіяння центра електричних навантажень.
9. Визначення та класифікація електричних переходів
10. Вимірювання активної потужності у трифазних електричних колах
11. Вимірювання електричних величин трифазної системи
12. Вимірювання реактивної потужності у трифазних електричних колах

Переглядів: 7514