• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Середня квадратична.

Використовується для визначення характеристики варіації ознак (наприклад, дисперсія) та для узагальнення ознак, виражених лінійними мірами площ (наприклад, при обчисленні середнього діаметру).

Середня квадратична буває двох видів:

– проста:

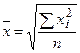
– зважена:

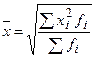
Вище вказані середні є узагальню вальними характеристиками сукупностей за тією чи іншою варіаційною ознакою. Водночас структуру цих сукупностей характеризують особливими показниками, які називаються у статистиці структурними середніми величинами. Зокрема, це мода та медіана.

Мода (М_о) – це величина, яка найчастіше трапляється в даній сукупності. У варіаційному ряді це – варіанта, якам має найбільшу частоту.

Моду широко використовують у комерційній діяльності, в соціологічних дослідженнях, коли вивчають ринковий попит, реєструють ціну, встановлюють рейтинг популярності осіб чи товарів тощо.

В інтервальному варіаційному ряді для знаходження модальної величини ознаки, що міститься в певному інтервалі, формула має такий вигляд:

,

де х₀ – нижня межа модального інтервалу;

h – ширина або шаг інтервалу;

f_m – частота модального інтервалу;

f_m-1 – частота інтервалу, що передує модальному;

f_m+1 – частота наступного за модальним інтервалу.

Медіана (М_е) – це варіанта, що є серединою впорядкованого варіаційного ряду, тобто ділить його на дів рівні частини: одна частина має значення варіаційної ознаки менше, ніж середня, а друга – більше. Медіана вказує на значення варіаційної ознаки, якого досягла половина одиниць сукупності.

Медіані у дискретному ряді визначають за сумою всіх частот, яку треба поділити на дві і до отриманого результату додати 0,5. У тому разі, коли сума частот парна, медіанна варіанта є дробовим числом, але оскільки дробових варіантів не буває, то медіана лежить у середині сусідніх варіантів.

Для обчислення медіани в інтервальному ряді визначають медіанний інтервал. Від відповідає такому, кумулятивна частота якого дорівнює або перевищує половину суми частот. Кумулятивні частота визначають за допомогою поступового підсумовування частот, розпочинаючи з інтервалу з найменшим значенням ознаки. Медіану розраховують за наступною формулою:

,

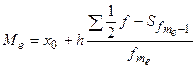де х₀ – нижня межа медіанного інтервалу;

h – ширина або шаг інтервалу;

f_mе – частота медіанного інтервалу;

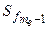– сума кумулятивних частот до медіанного інтервалу;

f – частоти ряду.

Читайте також:

1. VI. Середня кишка
2. VІ Середня хронологічна
3. Безпосередня і представницька демократія
4. БЕЗПОСЕРЕДНЯ ПІДГОТОВКА ХВОРОГО ДО ОПЕРАЦІЇ
5. В – середня тривалість додаткової відпустки одного працівника, що має
6. Видаток і середня швидкість ламінарного потоку.
7. Екскурсія-огляд вікна (середня група)
8. Ефективний діаметр молекул. Частота зіткнень та середня довжина вільного пробігу молекул
9. ЗАГАЛЬНА СЕРЕДНЯ ОСВІТА
10. Загальна середня освіта.
11. І Середня арифметична проста
12. ІІ Середня арифметична зважена

Переглядів: 527