• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поняття та види рядів розподілу.

Статистична сукупність формується під впливом причин та умов, з одного боку – типових, спільних для всіх елементів сукупності, а з іншого – випадкових, індивідуальних. Ці фактори пов’язані, а їх спільна взаємодія визначає як індивідуальні значення ознак, так і розподіл останніх у межах сукупності. Характерні властивості структури статистичної сукупності відбиваються в рядах розподілу.

Ряд розподілу складається з двох елементів:

1. варіанта – значення групувальної ознаки х_і;

2. частота – f_i..

Побудова рядів випливає з принципів статистичного групування. Ряди розподілу можна утворити або за атрибутивними, або за кількісними (варіаційними) ознаками.

При побудові атрибутивних рядів розподілу варіанти потрібно розташувати за логічною послідовністю.

Розрізняють ряди розподілу з абсолютними, відносними та нагромадженими частотами. Нагромаджені частоти називають кумулятивними, абсолютні частоти є абсолютними числами, а відносні – питомою вагою або часткою кожної групи.

Ряди розподілу з абсолютними частотами характеризують склад сукупності, а з відносними – їх структуру.

Ряди розподілу з кумулятивними частотами вказують на кількість або питому вагу одиниць із значенням ознаки, меншим від заданої. Кумулятивні частоти знаходять підсумуванням їх по групах.

Щільність розподілу – це кількість одиниць сукупності, що припадає на одиницю величини інтервалу групувальної ознаки. Розрізняють абсолютну ( 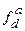) та відносну ( 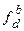) щільність, і відповідають наступним формулам:

; ,

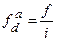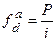де f – частота;

Р – частка (питома вага);

і – розмір інтервалу.

Інтерполяція в рядах розподілу визначає, скільки одиниць сукупності (або частка) мають значення ознаки, менше від заданого. Для інтерполяції використовують як абсолютні, так і відносні нагромаджені частоти.

Поглиблений аналіз закономірностей розподілу передбачає характеристику зазначених особливостей сукупності:

– визначення типового рівня ознаки, який є центром тяжіння;

– вимірювання варіації ознаки, ступеня згрупованості індивідуальних значень ознаки навколо центра розподілу;

– оцінка особливостей варіації, ступеня її відхилення від симетрії;

– оцінювання нерівномірності розподілу значень ознаки між окремими елементами сукупності, тобто ступінь їх концентрації.

Читайте також:

1. II. Поняття соціального процесу.
2. V. Поняття та ознаки (характеристики) злочинності
3. VII. Поняття про рану, рановий процес, види загоювання ран
4. А/. Поняття про судовий процес.
5. Адміністративна відповідальність: поняття, мета, функції, принципи та ознаки.
6. Адміністративний проступок: поняття, ознаки, види.
7. Адміністративні провадження: поняття, класифікація, стадії
8. Акти застосування юридичних норм: поняття, ознаки, види.
9. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
10. Аналітичні показники рядів динаміки.
11. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ
12. АРХІВНЕ ОПИСУВАННЯ: ПОНЯТТЯ, ВИДИ, ПРИНЦИПИ І МЕТОДИ

Переглядів: 653