Новини освіти і науки:

G+

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕПЕРІШНЯ ВАРТІСТЬ

Інвестиції окремих суб'єктів, що виступають на фінансовому ринку, чи фірм, що набувають майнові засоби, які необхідні для їхньої діяльності, ґрунтуються на видатках (затратах) грошових засобів сьогодні, взамін на потік майбутніх доходів.

Оцінка ефективності доступних можливостей інвестування повинна спиратися на порівняння вартості необхідних затрат з вартістю потоку очікуваних доходів. Оскільки потоки видатків і доходів, затрачених і отриманих пізніше, являють меншу вартість, ніж потік видатків і доходів, затрачених і отриманих раніше, то, здійснюючи ці підрахунки, мають враховувати цей факт, якщо відповідні інвестиційні рішення є раціональними.

Методом, який дозволяє привести видатки і доходи, затрачені і отримані в різні моменти розрахункового періоду, до порівняння на початок цього періоду, є метод дисконтування, котрий базується на перемножуванні номінальної вартості потоків видатків і доходів за різні періоди (роки) на відповідні коефіцієнти дисконтування.

Фінансовому менеджерові необхідно аналізувати теперішню вартість майбутніх доходів в таких, зокрема, випадках:

1) одноразові сплати, котрі сподіваються отримати у визначений момент у майбутньому;

2) потоки доходів (сплат), які сподіваються отримувати періодично (щорічно) протягом певного (обмеженого) періоду (років);

3) потоки доходів (сплат), котрі сподіваються отримувати щорічно, теоретично протягом нескінченного терміну (довічна рента).

Теперішня вартість грошей визначається за формулою

PV = FV_t / (l + r⁾^t, (9.21)

де PV — теперішня (поточна) вартість; FV_t — майбутній доход, котрий сподіваються отримати через t років; r — річна ставка дисконту; t — кількість років.

Теперішня вартість очікуваного потоку доходів залежить від розподілу щодо отримання цих доходів в часі, а також норми дисконту. Якщо є такі дані: FV_t — суми, котрі сплачуються в t-му проміжку часу в майбутньому; r — ставка дисконту; Т — кількість періодів (років), то теперішню вартість майбутнього потоку доходів можна обчислити за формулою

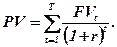(9.22)

Обчислення теперішньої вартості потоку грошових доходів за формулою (9.22), сподіваних у майбутньому протягом певної кількості років, є найчастіше використовуваним у фінансовому менеджменті випадком врахування чинників часу та ризику. Більшість рішень, що їх приймають інвестори, стосується порівняння обсягів сьогоднішніх затрат, взамін на потік сподіваних доходів протягом певної кількості років у майбутньому.

Це стосується, зокрема, і інвестиційних проектів, що їх збирається реалізувати фірма (підприємство), а також купівлі акцій, облігацій тощо.

Приклад.Компанія сподівається одержати доход 1 млн. крб. Визначити теперішню вартість цього доходу залежно від терміну, через який він надійде, та від величини ставки дисконту. Нехай термін приймає 11 різних значень, від 0 (поточний рік) до 10 (доход надійде через 10 років), а ставка дисконту може прийняти одне з трьох значень (5%, 8%, 10%).

Розв'язання.Користуючись формулою (9.21), одержимо результати (табл. 9.1).

Таблиця 9.1

t	r = 5%	r = 8%	r = 10%
	1 000 000	1 000 000	1 000 000
	952 381	925 926	909 091
	907 029	857 339	826 446
	863 838	793 832	751 315
	822 702	735 030	683 013
	783 527	680 583	620 921
	746 215	630 170	564 474
	710 681	583 490	513 158
	676 839	540 269	466 507
	644 609	500 249	424 098
	613 913	463 193	385 543

Ці результати можна подати у графічній формі. На рис. 9.3 зображено відповідні результати для випадку, коли t = 10 років.

Рис. 9.3. Теперішня вартість сподіваного у майбутньому доходу

Теперішня вартість потоку доходів, що сподіваються отримувати протягом певної кількості років у майбутньому, залежить від номінальної величини цих доходів (FV), норми дисконту (r), а також періоду, протягом якого ці доходи сподіваються отримувати.

Приклад.Компанія протягом 5 років сподівається щорічно отримувати доход 1 млн. крб. При цьому ставка дисконту може мати одне з трьох значень: 5%, 8%, 10%.

Розв'язання.Користуючись формулою (9.22), одержимо:

для r₁ = 5%:

PV₁ = 1 000 000 / (1 + 0,05)¹ + 1 000 000 / (1 + 0,05)² + 1 000 000 / (1 + 0,05)³ + 1 000 000 / (1 + 0,05)⁴ + + 1 000 000 / (1 + 0,05)⁵ = 952 381 + 907 029 + 863 838 + 822 702 + 783 527 = 4 329 477 крб.;

для r₂ = 8 %: PV₂ = 3 992 710 крб.;

для r₃ = 10 %: PV₃ = 3 790 786 крб.

Часто фінансовому менеджерові доводиться визначати теперішню вартість ануїтету.

Ануїтет— послідовність однакових за обсягом виплат за певні проміжки часу.

Ануїтетом можуть бути виплати або інвестиції щорічні, щопіврічні, щоквартальні, щомісячні. Кожна окрема виплата, що входить до складу ануїтету, називається його членом. Теперішню вартість Т — річного ануїтету можна обчислити за формулою

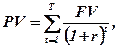(9.23)

де PV — теперішня вартість; FV — сума, що сплачується за певний проміжок часу (рік); r — ставка дисконту; Т — кількість років.

Приклад.Що вигідніше: одержати одночасно 50 млн. крб. готівкою, чи одержувати щорічно по 12 млн. крб. протягом 5 років за умови, що річна ставка складає 10% [34].

Розв'язання.У цьому випадку менеджер змушений визначити теперішню вартість ануїтету за формулою (9.23). У наведеному прикладі отримаємо

PV= 12 000 / (1 + 0,1)^{1 +}12 000 / (1 + 0,1)² + 12 000 / (1 + 0,1)³ + 12 000 / (1 + 0,1)⁴ + 12 000 / (1 + 0,1)⁵ = 45 492 тис. крб.

Оскільки 50 000 > 45 492, тому вигідніше вибрати варіант, що передбачає отримання відразу 50 млн. крб. готівкою, ніж мати щорічні надходження по 12 млн. крб. протягом 5 років.

Стосовно обчислений теперішньої вартості довічної ренти (ануїтету), коли сподіваний щорічний доход, очікуваний у майбутньому, приймають як сталу незалежну від часу величину FV_t = FV, з (9.23) маємо

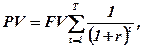(9.24)

Перемножуючи ліву і праву частини (9.24) на (1 + r), маємо

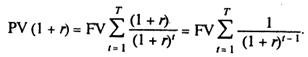
Віднімаючи від цього виразу вираз, поданий за формулою (9.24), одержимо

Якщо Т→∞, то 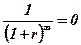i можна записати наступну формулу PVr = FV, або остаточно

PV=FV/r. (9.25)

Формула (9.25) для обчислення теперішньої вартості сподіваного потоку доходів застосовується до тих інвестицій, котрі не мають окресленого терміну існування (зростання). Типовим випадком таких інвестицій є купівля привілейованих акцій, що приносять їх власникові сталий щорічний доход.

Застосовують також формулу

P₀ = D/r_п,(9.26)

де Р₀ — теперішня ціна привілейованої акції; D — дивіденд від привілейованої акції; r_п— задана (обрана) інвестором норма доходу від привілейованої акції (норма дисконту) з урахуванням ризику.

Приклад. Дивіденди від привілейованої акції складають 10 тис. крб. річних. Обрана інвестором норма доходу від інвестиції, обтяженої приблизно таким же рівнем ризику, складає 10%. Обчислити теперішню вартість потоку дивідендів.

Розв'язання. Користуючись формулою (9.26), одержимо

Р₀ = 10 / 0,1 = 100 тис. крб.

Ринкову ціну звичайних акцій розрахувати дещо важче. Тут ще додатково необхідно спиратися на сподівання. Теперішня вартість звичайної акції визначається з урахуванням:

• розміру майбутніх прибутків (дивідендів), що припадають на одну акцію;

• ціни, яку сподіваються отримати від її продажу.

Часто вартість звичайної акції обчислюють як теперішню вартість потоку дивідендів, отримуваних починаючи з періоду t₁ до нескінченності:

(9.27)

де P₀ — теперішня вартість звичайної акції; D — сподівані дивіденди від звичайної акції; r — встановлена інвестором норма прибутків від звичайної акції (норма дисконту) з урахуванням ризику.

На практиці найчастіше користуються модифікацією (9.27), закладаючи стале зростання майбутніх дивідендів:

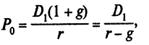(9.28)

де g — норма зростання дивідендів.

У цьому випадку приймають гіпотезу, що ціна звичайної акції залежить від розміру дивідендів, яку сподіваються одержати наприкінці періоду t₁ та норми зростання дивідендів у наступних періодах. Норма зростання, в свою чергу, залежить від кількох чинників, зокрема від прибутковості власного капіталу тощо.

Приклад. Нетто прибуток на одну акцію складає наприкінці періоду t₁ 25 тис. крб. Задана норма доходу інвестицій з таким самим ступенем ризику складає 15%, норма зростання дивідендів — 8 %.

Обчислити економічно обґрунтовану ціну даної акції.

Розв'язання. Використовуючи формулу (9.28), одержимо

P₀ = 25 / (0,15 - 0,08) = 25 / 0,07 = 357,14 тис. крб.

Читайте також:

<== попередня сторінка	\|	наступна сторінка ==>
ТЕХНІКА ДИСКОНТУВАННЯ. МАЙБУТНЯ ВАРТІСТЬ	\|	ОЦІНКА РИНКОВОЇ ВАРТОСТІ ПІДПРИЄМСТВА ТА РИЗИК

Не знайшли потрібну інформацію? Скористайтесь пошуком google:

Генерація сторінки за: 0.007 сек.