• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Тлумачний словник
Авто
Автоматизація
Архітектура
Астрономія
Аудит
Біологія
Будівництво
Бухгалтерія
Винахідництво
Виробництво
Військова справа
Генетика
Географія
Геологія
Господарство
Держава
Дім
Екологія
Економетрика
Економіка
Електроніка
Журналістика та ЗМІ
Зв'язок
Іноземні мови
Інформатика
Історія
Комп'ютери
Креслення
Кулінарія
Культура
Лексикологія
Література
Логіка
Маркетинг
Математика
Машинобудування
Медицина
Менеджмент
Метали і Зварювання
Механіка
Мистецтво
Музика
Населення
Освіта
Охорона безпеки життя
Охорона Праці
Педагогіка
Політика
Право
Програмування
Промисловість
Психологія
Радіо
Регилия
Соціологія
Спорт
Стандартизація
Технології
Торгівля
Туризм
Фізика
Фізіологія
Філософія
Фінанси
Хімія
Юриспунденкция

ТЕХНІКА ДИСКОНТУВАННЯ. МАЙБУТНЯ ВАРТІСТЬ

Більшість людей розуміє, що певна кількість грошей має сьогодні більшу вартість, ніж ті самі гроші, наприклад, через три роки. Як кажуть, що «гроші гублять вартість», тобто вартість грошей втрачається з часом навіть за нульової інфляції. Можна навести дві причини, що призводять до цього:

1. Ризик. Мільйон карбованців, одержаний сьогодні, має більшу вартість, ніж обіцяний (за відсутності інфляції) через рік. Різні причини можуть призвести до недотримання обіцянки. Тобто, одержання 1 млн. крб. через рік обтяжене ризиком.

2. Пріоритет поточного споживання. Людина надає пріоритет поточним приємним справам, а не майбутній радості.

Інвестування капіталу, зокрема в цінні папери, є прийняттям рішення щодо майбутнього. Тобто, йдеться про необхідність визначення ефективності рішень щодо майбутнього та порів­няння ефектів, що відносяться до різних моментів часу.

Для цього необхідно розглянути зміну вартості грошей за часом. Зробити це можна застосовуючи техніку дисконтування.

Техніка дисконтування спирається на математичні методи обчислення складного відсотка.

При цьому відсотки приєднуються до початкової бази (почат­кового капіталу), отже, база для визначення нарощеної суми змінюється. Механізм нарощування грошей по складних відсотках називають також капіталізацією відсотка.

Введемо позначення: Р — початковий капітал, r — норма відсотка, FV_t — вартість капіталу через t років.

Використовуючи той факт, що вартість капіталу через певний період дорівнює сумі вартості капіталу на початку цього періоду плюс відсоток, отриманий протягом цього періоду, одержимо схему вартості інвестованого капіталу:

на початку — Р;

через рік — FV₁ = Р+ rР = Р(1+ r);

через два роки — FV₂ = Р(1 + r) + [Р(1 + r)] r = Р(1 + r)(1 + r) = P(l + r⁾²;

через Т років — FV_T =P(1+r)^T. (9.16)

Наведені міркування дають основу для означення майбутньої вартості.

Майбутня вартість це вартість певної суми грошей, отри­маної в майбутньому шляхом застосування техніки складного відсотка до початкової суми грошей.

Тобто, майбутня вартість — це вартість інвестованого тепер капіталу у майбутньому.

Приклад. Інвестор вклав 2 млн. крб. у банк під 50% річних на 5 років. Відсотки складні. Якою буде сума майбутньої вартості інвестора по закінченні терміну?

Розв'язання. В цьому випадку Р = 2 млн. крб., r = 0,5, Т = 5.

За формулою (9.16) FV₅ = 15,1875 млн. крб.

Формула (9.16) показує, що майбутня вартість теперішньої суми грошей залежить від трьох чинників:

• початкової вартості (суми капіталу);
• тривалості інвестиційного періоду, протягом якого капітал приносить доход (відсоток);
• розміру норми відсотка.

Чим більший початковий капітал, тим більша майбутня вартість. Чим довший період інвестування, тим більша майбутня вартість. Чим більша норма відсотка, тим більша майбутня вартість.

Майбутня вартість виявляє сталий темп зростання капіталу з часом, причому цей темп дорівнює нормі відсотка. Рис. 9.2 показує залежність майбутньої вартості від довжини періоду інвестування для різних значень величини норми відсотка за умови, що початковий капітал дорівнює одиниці.

Бачимо, що залежність майбутньої вартості (представленої на осі ординат) вік кількості років (представленої на осі абсцис) має суттєвий характер. У випадку нульової величини норми відсотка майбутня вартість є константою, що дорівнює початковій вартості.

Формулу (9.16) можна інтерпретувати і по-іншому. Наприклад, необхідно визначити, за який період наш початковий капітал, що дорівнює Р, зросте у два рази (знаючи норму відсотка).

Рис. 9.2. Залежність майбутньої вартості від періоду інвестування

Це означає, що слід визначити довжину періоду Т, через який майбутня вартість дорівнюватиме 2Р.

За формулою (9.16) 2Р = Р(1 + r^)T.

Логарифмуючи обидві частини цього рівняння, одержимо

log 2 + log P = log P + T log (1 + r),

або

Т= log 2 / log (1 + r).

Можна довести, ,що необхідний для подвоєння капіталу період приблизно дорівнює

T = 0,7/r. (9.17)

Приклад. Маємо початковий капітал, що дорівнює 1 000 оди­ниць. Гроші вкладаються в банк за умови, що річна норма відсотка дорівнює 14%. Необхідно визначити, через який період початковий капітал подвоїться.

Розв'язання. В нашому випадку Р = 1000, r = 0,14.

Використовуючи формулу (9.17), одержимо T = 0,7/0,14 = 5 років.

Можна перевірити результат обчислень за наближеною фор­мулою, використовуючи формулу (9.16) (при T = 5):

FV₅ = 1925,4.

За умов інфляції банками передбачені змінювані за часом ставки складних відсотків. У таких ситуаціях майбутня вартість обчислюється за формулою

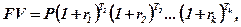(9.18)

де r₁, r₂, ..., r_k — норми відсотка (відсоткові ставки), T₁, Т₂ , ..., T_k — періоди.

Змінювані ставки слід відрізняти від «плаваючих», розміри котрих невідомі.

Приклад.Банк стягує за позику 5 млн. крб. 40% річних. За другий рік встановлена банком маржа складає 2%, за кожен наступний рік — 3%. Термін позики 5 років. Визначити доход банку.

Розв'язання.Користуючись формулою (9.18), знаходимо май­бутню вартість (обсяг поверненого боргу через 5 років):

FV₅ = 29,06655 млн. крб.

Доход банку становить

FV₅ - P = 24,06655 млн. крб.

Наведені вище міркування стосуються ситуації, коли капі­талізація відсотків проводиться раз на рік. Очевидно, що для багатьох фінансових інструментів, наприклад облігацій чи термі­нових банківських вкладів, відсотки додаються до капіталу час­тіше. У випадку, коли відсотки додаються до капіталу т раз протягом року (за рівні періоди), отримуємо наступну формулу майбутньої вартості по Т роках:

FV_T = P(1+r/m)^mT. (9.19)

Зазначимо, що формула (9.16) є частковим випадком (9.19), коли т =1, тобто коли відсотки капіталізуються раз на рік.

Приклад.Початковий капітал становить 2 000 одиниць, річна норма відсотка складає 5%, а відсотки долучаються до капіталу через кожні півроку.

Обчислити, якою буде майбутня вартість через рік та через 5 років.

Розв'язання.Маємо Р = 2 000, r = 0,05, т = 2.

Згідно з цим за формулою (9.19) отримаємо

FV₁ = 2101,25; FV₅ = 2560,168.

Врешті при застосуванні гіпотетичної неперервної (тобто в кожен момент часу) капіталізації відсотків, одержимо формулу для обчислення майбутньої вартості

FV_T = Pe^rT,(9.20)

де e — константа, основа натуральних логарифмів (е = 2,7183).

Читайте також:

1. IV. Агротехніка квітково-декоративних рослин відкритого грунту.
2. IV. Вартість знака для товарів і послуг та фірмового найменування
3. IV. ТИМЧАСОВА ВАРТІСТЬ ГРОШЕЙ
4. V теорія граничної корисності визначає вартість товарів ступенем корисності останньої одиниці товару для споживача.
5. Агротехніка вирощування сіянців модрини
6. Агротехніка вирощування сіянців ялини
7. Альтернативна вартість і незворотні витрати
8. Альтернативна вартість та її використання у проектному аналізі
9. АНТИЧНА НАУКА І ТЕХНІКА
10. Архаїчна техніка
11. Б) Вартість і ціна.
12. Б. Новостворена вартість, яка складається з вартості необхідного продукту (НП) і вартості додаткового продукту ( ДП).

Переглядів: 815