• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Поляризація густих газів, рідин та твердих тіл. Поле Лоренца

Теорії електронної, іонної і орієнтаційної поляризації, розглянуті нами раніше, справедливі лише для розріджених газів. Для кожного окремого атому ми покладали, що його дипольний момент

,

де 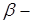поляризовність атому, 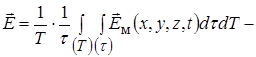напруженість електричного поля в діелектрику, яка є усередненим значенням по всіх мікроскопічних полях всередині діелектрика та у часі.

Простий аналіз виявляє помилку в цих міркуваннях. Поле в діелектрику є сумою зовнішнього поля 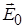і усередненого по простору і в часі поля зв’язаних зарядів, тобто поля всіх диполів, з яких складається діелектрик, включаючи і той диполь, для якого ми обчислюємо 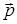. Між тим, сам диполь на себе не діє. Замість поля 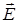в формулу для дипольного моменту атома необхідно підставити так зване діюче (або локальне) поле 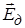. Це поле є векторною сумою зовнішнього поля 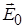і поля всіх інших диполів, виключаючи вибраний нами. Щоб записати його, скористаємось виразом для потенціалу диполя

.

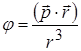Оскільки 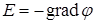, то

.

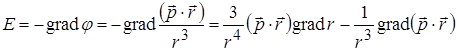Зробимо очевидні перетворення

,

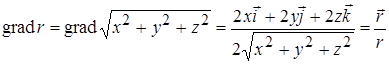і

,

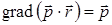тоді поле кожного диполя

.

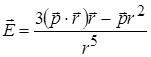Тоді вираз для діючого поля набуває вигляду

,

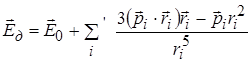де дипольний момент довільного диполя, а радіус-вектор, проведений з точки, де він знаходиться, в точку, де ми знаходимо 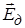. Штрих в сумі показує, що поле диполя, який знаходиться в шуканій точці, не враховується.

Далі ми покажемо, що для густих газів, рідин та твердих тіл поле в діелектрику 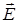і діюче поле 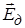помітно відрізняються, а для розріджених газів поле в діелектрику приблизно дорівнює діючому полю .

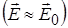Діюче поле легко записати у загальному вигляді, але складно обчислити. Лоренц запропонував простий метод, який дозволяє обчислити діюче поле для газів, рідин і кубічних кристалів, тобто для широкого кола діелектриків. Для кристалів не кубічних сингоній цей метод незастосовний. Розглянемо суть методу Лоренца.

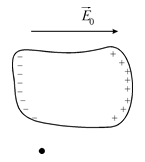Раніше при розрахунку поля в діелектрику ми вважали, що в однорідно поляризованому діелектрику поля всіх диполів, які знаходяться в об’ємі, взаємно компенсують одне одного, тому достатньо враховувати тільки ті заряди, які виходять на поверхню. На жаль, це справедливо лише для точки, яка лежить зовні і досить далеко від діелектрика.

У нашому випадку цим методом користуватись не можна, оскільки точка, у якій ми шукаємо поле 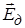, лежить всередині діелектрика. Поля диполів, які знаходяться поблизу цієї точки, можуть не компенсувати одне одного.

Лоренц запропонував уявно оточити точку, в якій ми обчислюємо 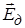, сферою такого радіусу, щоб він був достатньо великий порівняно із відстанями між диполями, і достатньо малий, щоб поле у сфері можна було вважати однорідним. В такій сфері знаходиться багато диполів.

Якщо вилучити речовину діелектрика, яка знаходиться у сфері, в діелектрику утвориться порожнина. Для диполів поза сферою картина на зміниться, для них можна не враховувати поле диполів всередині сфери, і її вилучення може впливати (далі покажемо, що й не завжди) лише на поле у виділеному уявному сферичному околі.

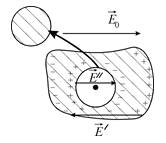Тоді діюче поле у околі виділеної точки складається з

,

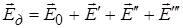де

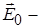зовнішнє електричне поле;

поле, створене поляризаційним зарядом на зовнішній поверхні діелектрика;

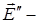поле поляризаційних зарядів на внутрішній поверхні уявної сферичної порожнини (поле Лоренца). Воно діє на атом у центрі порожнини. Введення такої порожнини є лише математичним прийомом розрахунку поля Лоренца;

поле диполів всередині уявної сфери.

Решта диполів у проміжках між поверхнями компенсують поля один одного. Але 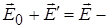не що інше, як поле у діелектрику, яким ми користувались раніше, до нього тепер додались два доданки, утворюючи діюче поле.

А задачу про поле у порожнині в діелектрику ви повинні були розв’язати у задачах, винесених на самостійне опрацювання. (На лекції не наводити!)

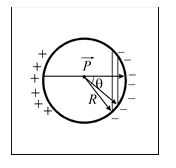
Вперше її розв’язав Лоренц у 1879 році. Якщо через 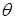позначити полярний кут, який будемо відраховувати від напрямку поляризації 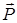як від осі, то густина поверхневого заряду в околі точки, що задається радіус-вектором, направленим під кутом 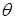, становить 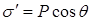. Поверхневий заряд буде однаковий симетрично відносно осі 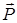, тому кільце радіусом і завширшки 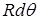(тобто із площею 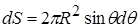) із зарядом

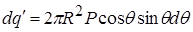
створить у центрі порожнини поле

.

Ще один 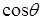з’явився тому, що складові поля вздовж осі поляризації додаються, а перпендикулярні їй – взаємно знищуються. Повне електричне поле у центрі порожнини становитиме

.

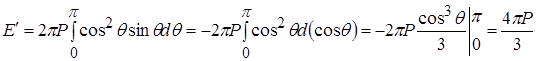Отже, поле Лоренца поле у порожнині в діелектрику, де 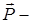вектор поляризації. Тоді

.

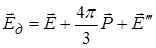Тепер треба врахувати ті диполі, які знаходяться всередині видаленої кулі, і дають поле 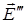, яке треба обчислити. Лоренц показав, що для газів, рідин та кубічних кристалів 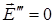, тому діюче поле набуває вигляду в системі Гаусса

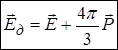, (система CGSE)

і є сумою середнього поля у діелектрику та доданку, пов’язаного із нескомпенсованістю локальних полів диполів. В системі СІ діюче поле має вигляд

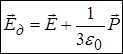. (cистема СІ)

Таке діюче поле легко порахувати, якщо насправді .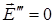

Доведемо за Лоренцом, що

.

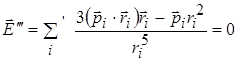Розглянемо кристал з кубічною граткою і візьмемо точку у центрі видаленої сфери. Нагадаю, що сума береться по всіх диполях в межах сфери, виключаючи диполь у виділеній точці, тому біля знаку суми ставимо штрих. Відкинемо індекс 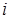для зручності, виберемо початок координат в центрі сфери. Тоді проекція 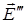на вісь 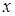має вигляд

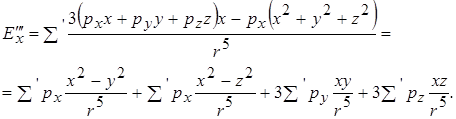
Розглянемо окремо суму

.

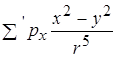Нехай в кубічному кристалі всередині сфери в точці з координатами 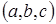знаходиться диполь, тобто ця точка – вузол кубічної гратки. Тоді точка з координатами 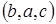також належить гратці, і в ній знаходиться диполь. У вибраній нами сумі доданки, що відносяться до цих двох точок, взаємно скоротяться. Так можна поступити з усіма точками всередині сфери, в яких знаходяться диполі, і показати, що

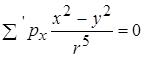
Для рідин і газів результат буде таким же, треба лише, вибравши точку 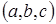, врахувати, що в точці 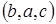з тією ж імовірністю буде знаходитись диполь.

Аналогічно доводиться рівність нулю всіх інших сум. Для 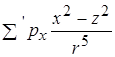треба лише точці 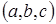зіставити точку , в сумі точку 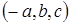, і т.п. Показавши, що 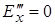, подібним чином можна одержати 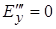і 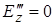. Отже, в кубічному кристалі та рідинах і стиснутих газах .

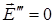Визначивши 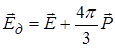, можна записати дипольний момент атому

.

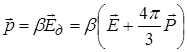Тоді вектор поляризації

,

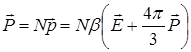звідки

.

Але 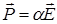, тоді діелектрична сприйнятливість і діелектрична проникність

, .

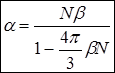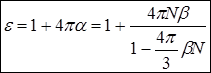Ви будете сміятись, але остання отримана формула називається формулою Лоренц-Лоренца. Її отримали незалежно в 1869 році датський фізик-теоретик Людвиг Валентин Лоренц і в 1880 році нідерландський фізик-теоретик Хендрик Антон Лоренц (перетворення Лоренца, сила лоренца – його).

А ось тепер я вам чесно зізнаюся, що не знайшла, який саме Лоренц запропонував розглянутий метод.

Проаналізуємо формулу Лоренц-Лоренца. Концентрація 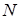пов’язана із середньою відстанню між частинками 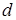співвідношенням 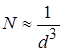, поляризовність 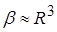, де 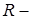радіус атому, тоді . Для розріджених газів 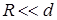, тому 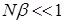, і 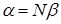, , 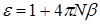тобто ми одержали попередній результат для розріджених разів, відповідно, 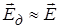. Для густих газів, рідин та твердих тіл , тому необхідно враховувати різницю між 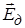і .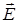

Читайте також:

1. L2.T4. Транспортування рідких, твердих та газоподібних речовин.
2. L2.T4/1.Переміщення твердих речовин по території хімічного підприємства.
3. L3.T4/2. Засоби переміщення рідин.
4. Аеровані промивальні рідини
5. Види діелектриків. Застосування твердих діелектриків в енергетиці.
6. Види течії в’язкої рідини
7. Визначення положення газорідинних і водо-нафтових контактів
8. Вимірювання хімічного складу і концентрації рідини
9. Вимірювання хімічного складу рідин
10. Витікання рідини через отвори та насадки
11. Вплив дійсного характеру руху рідини в робочому колесі на теоретичний напір насоса
12. Вплив промивальної рідини на колекторські властивості продуктивного пласта

Переглядів: 782