• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Техніка знаходжень переміщень

Визначення переміщень значно спрощується застосуванням спеціальних методів обчислення інтегралу виду . Так, як в підінтегральний вираз входить добуток ординат епюр М_m і М_n , то цей метод називається способом множення епюр. Він може бути використаний, якщо одна з епюр, наприклад М_m, прямолінійна, а інша епюра може бути прямолінійною, ломаною або криволінійною.

Рис. 8.8

В цьому випадку

;

величини х і показані на рис.8.8. Підставивши значення 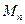у вираз , отримаємо

,

де 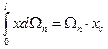- статичний момент площі епюри 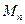відносно осі О-О.

Тоді .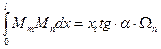

Але так як

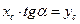
то

.

Значить, результатом множення двох епюр є добуток площі однієї з них на ординату другої (обов”язково прямолінійної) епюри, взяту під центром ваги площі першої епюри - правило або спосіб Верещагіна. При множенні ставиться знак плюс, якщо епюра і ордината під центром її ваги, взята з дркгої епюри, мають одинакові знаки, і мінус, - якщо різні знаки. В табл.1 приведені значення площ і координати центрів ваги найбільш поширених фігур.

В деяких випадках (рис. 8.9), якщо криволінійна епюра окреслена по параболі не вище другого степеня, більш доцільно користуватися формолою Сімпсона-Корноухова :

.

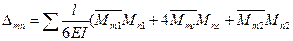Рис. 8.9.

Значення площ і координати центрів ваги найбільш поширених фігур.

Таблиця 1

При необхідності перемножити дві епюри, які мають вигляд трапецій, зручніше одну з епюр розбити на два трикутники і перемножити площі кожного з них на ординату під центром його ваги з другої епюри. При цьому отримаємо

= l/6(2ac+2bd+ad+bc).

Тут в дужках сумуються подвоєні добутки лівих ординат епюр, подвоєні добутки правих ординат епюр, добуток лівої ординати першої епюри на праву другої і добуток правої ординати першої епюри на ліву другої.

Читайте також:

1. IV. Агротехніка квітково-декоративних рослин відкритого грунту.
2. Агротехніка вирощування сіянців модрини
3. Агротехніка вирощування сіянців ялини
4. АНТИЧНА НАУКА І ТЕХНІКА
5. Архаїчна техніка
6. Визначення переміщень
7. Визначення переміщень у статично невизначуваних системах
8. Вимірювання кутових переміщень
9. Вимірювання лінійних переміщень, вібрацій та деформацій
10. Вимірювання переміщень.
11. Готельні номери оснащують наступними побутовими приладами: аудіо- та відеотехніка, фени, праски, чайники та ін.
12. Довідкові дані до визначення переміщень графічними методами

Переглядів: 996