• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Визначення переміщень у статично невизначуваних системах

Визначивши зайві невідомі зусилля, переміщення в статично невизначуваних системах можна знайти звичайними способами. При цьому слід користуватися методами, які в кожному окремому випадку найбільш про­сто приводять до результату. Наприклад, прогини та кути повороту пере­різів статично невизначуваних балок, що несуть складне навантаження, зручно визначати за методом початкових параметрів. Спосіб Мора, що є універсальним, може застосовуватися в усіх випадках. Ним широко ко­ристуються при визначенні переміщень у балках, рамах, фермах.

Обчислюючи переміщення за формулою Мора

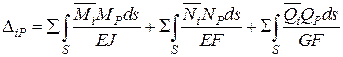. (3.4)

слід розглянути задану систему під дією навантаження (остаточні епюри силових факторів М, N та Q статично невизначуваної системи), а також під дією одиничного силового фактора, що відповідає шуканому переміщенню (одиничні епюри 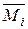, , 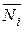). Якщо при цьому одиничні навантаження прикладати безпосередньо до заданої статично невизначуваної системи, то кожен раз для побудови одиничних епюр 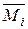, , 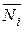зно­ву доведеться розв'язувати статично невизначувану задачу. Однак цього можна уникнути, якщо врахувати, що вихідна статично невизначувана система й основна статично визначувана, навантажена заданими силами та знайденими зайвими невідомими, повністю тотожні за умовами роботи. Тому, визначаючи будь-яке переміщення, ми маємо право прикладати оди­ничне навантаження до основної статично невизначуваної системи. Ос­тання може бути вибрана за будь-яким можливим варіантом.

Як приклад обчислимо взаємні переміщення точок А_1­, А­₂ та В₁, В₂ відповідно в горизонтальному та вертикальному напрямах для рами (рис. 3.8, а).

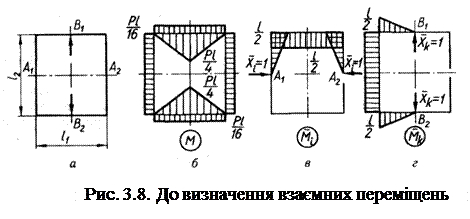
Визначимо лише переміщення, спричинені згинанням, оскіль­ки переміщеннями від поздовжніх деформацій та зсуву можна знехтува­ти. На рис. 3.8, б наведено складові сумарної епюри згинальних моментів у вигляді, зручному для застосування способу Верещагіна.

Для визначення взаємного переміщення в горизонтальному напрямі точок А_1­, А­₂ прикладаємо до основної системи в цих точках (рис. 3.8, в) одиничні сили 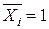. Перемножуючи епюри М та 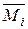і вважаючи, що l₁ = l₂ = l знаходимо

.

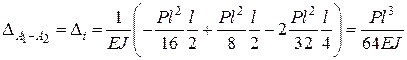Щоб визначити взаємне вертикальне переміщення точок В₁ та В₂,прикладаємо до основної системи в цих точках дві одиничні сили 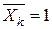(рис. 3.8, г). Перемножуючи епюри М та 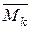, знаходимо, що

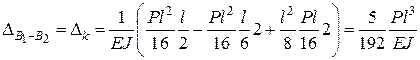
Читайте також:

1. I визначення впливу окремих факторів
2. II. Визначення мети запровадження конкретної ВЕЗ з ураху­ванням її виду.
3. II. Мотивація навчальної діяльності. Визначення теми і мети уроку
4. Ocнoвнi визначення здоров'я
5. Автоматизація водорозподілу на відкритих зрошувальних системах. Методи керування водорозподілом. Вимірювання рівня води. Вимірювання витрати.
6. Алгебраїчний спосіб визначення точки беззбитковості
7. Аналіз службового призначення деталей та конструктивних елементів обладнання харчових виробництві, визначення технічних вимог і норм точності при їх виготовленні
8. Аналіз стратегічних альтернатив та визначення оптимальної стратегії формування фінансових ресурсів
9. Аналіз ступеня вільності механізму. Наведемо визначення механізму, враховуючи нові поняття.
10. Арифметичні операції в різних системах числення
11. Багатопрольотні статично визначні балки
12. Балансова теорія визначення статі. Диференціація статі і роль гормонів у цьому процесі.

Переглядів: 1208