• Гідрологія і Гідрометрія
• Господарське право
• Економіка будівництва
• Економіка природокористування
• Економічна теорія
• Земельне право
• Історія України
• Кримінально виконавче право
• Медична радіологія
• Методи аналізу
• Міжнародне приватне право
• Міжнародний маркетинг
• Основи екології
• Предмет Політологія
• Соціальне страхування
• Технічні засоби організації дорожнього руху
• Товарознавство продовольчих товарів

Переміщення від зміни температури

Формула Мора може бути подана у вигляді

де 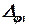= M_ndx/EJ — взаємний кут повороту торцевих перерізів елемента dx стержня від заданого навантаження; = N_ndx/EF — взаємний зсув їх у напрямі осі стержня; 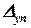= 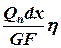i — взаємний зсув їх у напрямі нормалі до осі стержня.

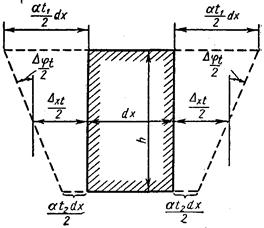
Рис. 8.7

У такому вигляді формула Мора може бути використана, коли деформації 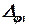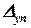елемента dx стержня викликані не тільки внутрішніми зусиллями в його поперечних перерізах від навантаження, але і дією температури на споруду. Отже, формулою Мора в приведеному вигляді можна користуватися і для визначення переміщень системи, викликаних дією температури.

Хай верхнє волокно елемента dx нагріто на t₁, а нижнє — на t₂ (рис. 8.7). Розподіл температури по висоті поперечного перетину приймемо по прямолінійному закону.

При температурному коефіцієнті лінійного розширення а подовження верхнього волокна рівно at₁dx, а подовження нижнього волокна at₂dx. Осьове подовження D_xn=D_xt можна отримати як середнє арифметичне вказаних величин (при поперечному перерізі, симетричному щодо горизонтальної осі):

.

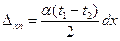Кут взаємного повороту крайніх поперечних перетинів (елемента dx) рівний:

.

Деформації зсуву в елементі dx від дії температури не виникають, тобто D_yn = 0.

Підставивши знайдені значення, отримаємо формулу для знаходження температурних перемещень:

.

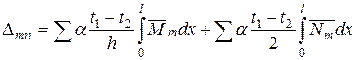Знаки Σ означають підсумовування по всіх стержнях і ділянках споруди. При обчисленні переміщення D_mt інтегрування поширюється лиш на ті елементи споруди, температурний режим яких змінився.

Для випадку прямолінійних або ламаних стержнів постійного перерізу інтеграли можуть бути підраховані як площі одиничних епюр, і формула переміщень приймає простий вигляд:

.

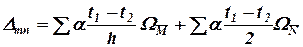Знаки членів формули D_mt визначають так: якщо деформації елемента dx від температури і одиничної сили одинакові, то й знак відповідного члена буде додатнім, і навпаки.

При визначенні переміщень від дії на споруду температури не можна нехтувати членом формули, залежним від подовжньої сили.

Читайте також:

1. IV. Критерій питомої потенціальної енергії деформації формозміни
2. L2.T4/1.Переміщення твердих речовин по території хімічного підприємства.
3. L3.T4/2. Засоби переміщення рідин.
4. А. Без зміни хазяїна та ендогенної агломерації
5. А. Без зміни хазяїна та ендогенної агломерації
6. АДАПТАЦІЯ ОПЕРАЦІЙНОЇ СИСТЕМИ ДО ЗМІНИ ЇЇ ЗАВАНТАЖЕННЯ.
7. Адміністративні зміни кінця 18-19 ст. та утворення нових архівів
8. Адміністративно-політичний устрій Української козацької держави середини XVII ст. Зміни в соціально-економічних відносинах
9. Адміністративно-політичний устрій Української козацької держави середини XVII ст. Зміни в соціально-економічних відносинах
10. Алгоритм розрахунку температури поверхні чипу ІМС процесора
11. Аналіз чутливості рівня беззбитковості до зміни основних факторів
12. Атмосферний тиск повітря, та його зміни з висотою та горизонтально

Переглядів: 1032